福建省泉州市南安实验中学2022-2023学年八年级下学期期中考试数学试卷

这是一份福建省泉州市南安实验中学2022-2023学年八年级下学期期中考试数学试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（4分）下列式子是分式的是（ ）
A．B．C．D．
2．（4分）在平面直角坐标系中，点（1，﹣2）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
3．（4分）若反比例函数的图象经过点（1，﹣2），则k＝（ ）
A．﹣2B．2C．D．﹣
4．（4分）若把分式：中的x和y都扩大2倍，那么分式的值（ ）
A．不变B．扩大2倍C．缩小2倍D．扩大4倍
5．（4分）已知是正比例函数，则m的值是（ ）
A．8B．4C．±3D．3
6．（4分）如图，函数y＝ax+b和y＝kx的图象交于点P，则根据图象可知二元一次方程组的解是（ ）
A．B．
C．D．
7．（4分）▱ABCD中，∠A+∠C＝220°，则∠B的度数是（ ）
A．60°B．70°C．100°D．110°
8．（4分）若关于x的分式方程＝3+有增根，则m的值是（ ）
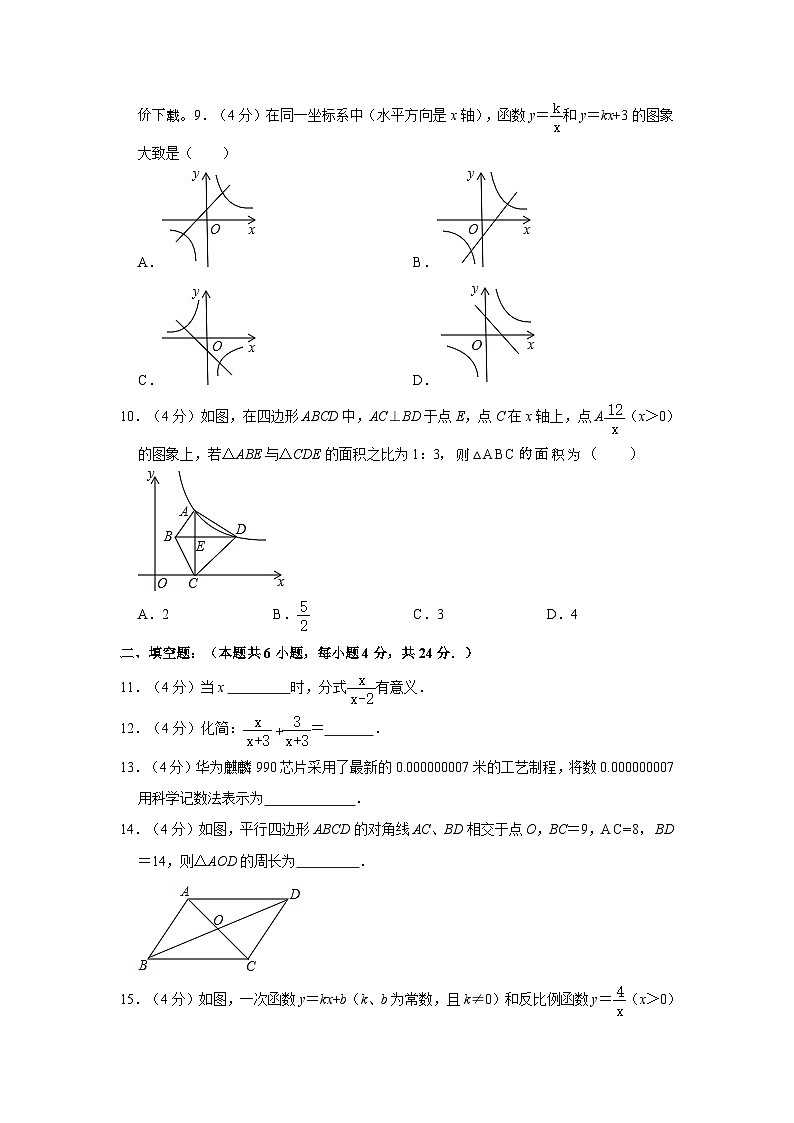
A．﹣2B．2C．±2D．4该试卷源自 每日更新，享更低价下载。9．（4分）在同一坐标系中（水平方向是x轴），函数y＝和y＝kx+3的图象大致是（ ）
A．B．
C．D．
10．（4分）如图，在四边形ABCD中，AC⊥BD于点E，点C在x轴上，点A（x＞0）的图象上，若△ABE与△CDE的面积之比为1：3，则△ABC的面积为（ ）
A．2B．C．3D．4
二、填空题：（本题共6小题，每小题4分，共24分．）
11．（4分）当x 时，分式有意义．
12．（4分）化简：＝ ．
13．（4分）华为麒麟990芯片采用了最新的0.000000007米的工艺制程，将数0.000000007用科学记数法表示为 ．
14．（4分）如图，平行四边形ABCD的对角线AC、BD相交于点O，BC＝9，AC=8，BD＝14，则△AOD的周长为 ．
15．（4分）如图，一次函数y＝kx+b（k、b为常数，且k≠0）和反比例函数y＝（x＞0）的图象交于A、B两点，利用函数图象直接写出不等式＜kx+b的解集是 ．
16．（4分）如图，在平面直角坐标系xOy中，点B（﹣1，4）（﹣7，0），点P是直线y＝x﹣2上一点，且∠ABP＝45°，则点P的坐标为 ．
三、解答题：（本大题共9小题，共86分。解答应写出文字说明，证明过程或演算步骤。在答题卡的相应位置内作答.）
17．（8分）计算：．
18．（8分）解方程：+3＝．
19．（8分）先化简，再求值：，其中x＝2023．
20．（8分）如图，E，F是▱ABCD的对角线AC上两点，且AF＝CE
21．（8分）学校为落实“新中考”中关于球类项目的测评方案，欲购进一批足球和排球，补充体育活动器材，用4500元购进足球和4000元购进排球的数量相同．
（1）每个足球和排球的进价分别是多少？
（2）学校准备购进足球和排球共100个，其中排球数量不超过足球数量的3倍，请你设计一种购买方案，最低费用为多少元？
22．（10分）如图，在平面直角坐标系中，▱ABCD的顶点A、B、D的坐标分别为（﹣3，0）、（1，0）、（0，4），反比例函数y＝的图象经过点C．
（1）求反比例函数的解析式．
（2）连结OC，若点P是反比例函数y＝的图象上的一点，求点P的坐标．
23．（10分）小明和小红同时从学校出发骑自行车到公园后返回，他们与学校的距离y（千米）和离开学校的时间x（分钟）
请根据图象回答：
（1）如果小明两次经过途中某一地点的时间间隔为15分钟，求该地与学校的距离；
（2）若小红出发35分钟后两人相遇，求小红从公园回到学校所用的时间．
24．（12分）如图1，平面直角坐标系中，直线y＝﹣x+6与x轴交于点A，与直线y＝2x交于点C．
（1）求点C的坐标．
（2）如图2，过点E作直线l⊥x轴于点E，交直线y＝2x于点F，若点E的坐标是（4，0），点M为y轴上OB的中点，使PM﹣PC的值最大？若存在，求出这个最大值，说明理由；
（3）若（2）中的点E是x轴上的一个动点，点的横坐标为m（m＞0），当m取何值时，直线l上存在点Q，C，Q为顶点的三角形与△AOC全等？请画出草图，并直接写出相应的m的值．
25．（14分）如图，在平面直角坐标系中，直线y＝kx+n（n＜0）（m＞0）的图象交于第一象限的点A，与x轴、y轴分别交于点B、C．
（1）若n＝﹣1，点A的坐标为（2，3）．
①直接填空：m的值为 ，k的值为 ；
②点P是x轴上一点，若△PAC的面积为6，求点P的坐标；
（2）过点M（1，0）作y轴的平行线l与函数y＝的图象交于点D（x＞0）的图象相交于点E．过点D作x轴的平行线与直线y＝kx+n交于点P（点P、D不重合）．问：当k为何值时
参考答案与试题解析
一、选择题：（本题共10小题，每小题4分，共40分）
1．（4分）下列式子是分式的是（ ）
A．B．C．D．
【解答】解：A、的分母中均不含有字母，而不是分式；
B、分母中含有字母．故本选项正确；
C、分母没有字母；
D、分母中没有字母是整式；
故选：B．
2．（4分）在平面直角坐标系中，点（1，﹣2）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：∵1＞0，﹣5＜0，
∴在平面直角坐标系中，点（1．
故选：D．
3．（4分）若反比例函数的图象经过点（1，﹣2），则k＝（ ）
A．﹣2B．2C．D．﹣
【解答】解：∵点（1，﹣2）在反比例函数y＝，
∴点P（7，﹣2）满足反比例函数的解析式y＝，
∴﹣2＝，
解得k＝﹣2．
故选：A．
4．（4分）若把分式：中的x和y都扩大2倍，那么分式的值（ ）
A．不变B．扩大2倍C．缩小2倍D．扩大4倍
【解答】解：分别用2x和2y去代换原分式中的x和y，
得＝，
可见新分式是原分式的．
故选：C．
5．（4分）已知是正比例函数，则m的值是（ ）
A．8B．4C．±3D．3
【解答】解：∵y＝（m+3）是正比例函数，
∴m2﹣8＝5且m+3≠0，
解得m＝8．
故选：D．
6．（4分）如图，函数y＝ax+b和y＝kx的图象交于点P，则根据图象可知二元一次方程组的解是（ ）
A．B．
C．D．
【解答】解：∵函数y＝ax+b和y＝kx的图象交于点P（﹣3，﹣2），
∴二元一次方程组的解是，
故选：B．
7．（4分）▱ABCD中，∠A+∠C＝220°，则∠B的度数是（ ）
A．60°B．70°C．100°D．110°
【解答】解：∵四边形ABCD是平行四边形，
∴∠A＝∠C，AB∥CD，
∵∠A+∠C＝220°，
∴∠A＝∠C＝110°，
∴∠B＝180°﹣∠A＝70°．
故选：B．
8．（4分）若关于x的分式方程＝3+有增根，则m的值是（ ）
A．﹣2B．2C．±2D．4
【解答】解：方程两边都乘（x﹣4），得
2＝3（x﹣4）﹣m
∵当最简公分母x﹣4＝8时，方程有增根，
∴把x﹣4＝0代入整式方程，
∴m＝﹣8．
故选：A．
9．（4分）在同一坐标系中（水平方向是x轴），函数y＝和y＝kx+3的图象大致是（ ）
A．B．
C．D．
【解答】解：A、由函数y＝，故A选项正确；
B、因为y＝kx+3的图象交y轴于正半轴；
C、因为y＝kx+3的图象交y轴于正半轴；
D、由函数y＝，故D选项错误．
故选：A．
10．（4分）如图，在四边形ABCD中，AC⊥BD于点E，点C在x轴上，点A（x＞0）的图象上，若△ABE与△CDE的面积之比为1：3，，则△ABC的面积为（ ）
A．2B．C．3D．4
【解答】解：设A（a，），D（b，），）
∵△ABE与△CDE的面积之比为1：3，
∴•（a﹣c）•（﹣•（b﹣a）•，
∴（a﹣c）•，
故选：A．
二、填空题：（本题共6小题，每小题4分，共24分．）
11．（4分）当x ≠2 时，分式有意义．
【解答】解：根据题意得：x﹣2≠0
解得：x≠8．
故答案为：≠2．
12．（4分）化简：＝ 1 ．
【解答】解：原式＝＝3，
故答案为：1
13．（4分）华为麒麟990芯片采用了最新的0.000000007米的工艺制程，将数0.000000007用科学记数法表示为 7×10﹣9 ．
【解答】解：0.000000007＝7×10﹣9．
故答案为：7×10﹣9．
14．（4分）如图，平行四边形ABCD的对角线AC、BD相交于点O，BC＝9，BC＝9，BD＝14，则△AOD的周长为 20 ．
【解答】解：∵四边形ABCD是平行四边形，
∴AD＝BC，OA＝OC，
∵BC＝9，BD＝14，
∴AD＝9，OA＝3，
∴△AOD的周长为：AD+OA+OD＝20．
故答案为：20．
15．（4分）如图，一次函数y＝kx+b（k、b为常数，且k≠0）和反比例函数y＝（x＞0）的图象交于A、B两点，利用函数图象直接写出不等式＜kx+b的解集是 1＜x＜4 ．
【解答】解：∵由图象可知：A（1，4），4），
∴不等式＜kx+b的解集为1＜x＜4，
故答案为：1＜x＜4．
16．（4分）如图，在平面直角坐标系xOy中，点B（﹣1，4）（﹣7，0），点P是直线y＝x﹣2上一点，且∠ABP＝45°，则点P的坐标为 ，） ．
【解答】解：将线段BA绕点B逆时针旋转90°得到线段BA′，则A′（3，
取AA′的中点K（﹣2，﹣2），
直线BK与直线y＝x﹣2的交点即为点P．
∵直线BK的解析式为y＝5x+3，
由，解得，
∴点P坐标为（﹣，﹣），
故答案为（﹣，﹣）．
三、解答题：（本大题共9小题，共86分。解答应写出文字说明，证明过程或演算步骤。在答题卡的相应位置内作答.）
17．（8分）计算：．
【解答】解：
＝1﹣3+4
＝4．
18．（8分）解方程：+3＝．
【解答】解：方程两边都乘（x﹣2），得
1+6（x﹣2）＝x﹣1，
解得x＝2
．
经检验x＝2为增根，原方程无解．
19．（8分）先化简，再求值：，其中x＝2023．
【解答】解：
＝•
＝x+8，
当x＝2023时，原式＝2024．
20．（8分）如图，E，F是▱ABCD的对角线AC上两点，且AF＝CE
【解答】证明：∵四边形ABCD是平行四边形，
∴AD＝CB，AD∥CB，
∴∠DAF＝∠BCE，
在△ADF和△CBE中，
，
∴△ADF≌△CBE（ SAS），
∴DF＝BE．
21．（8分）学校为落实“新中考”中关于球类项目的测评方案，欲购进一批足球和排球，补充体育活动器材，用4500元购进足球和4000元购进排球的数量相同．
（1）每个足球和排球的进价分别是多少？
（2）学校准备购进足球和排球共100个，其中排球数量不超过足球数量的3倍，请你设计一种购买方案，最低费用为多少元？
【解答】解：（1）设每个排球的价格为x元，则每个足球的价格为（x+10）元．
由题意得：，
解得：x＝80，
经检验，x＝80是原方程的解，
则x+10＝90，
答：每个足球的价格为90元，每个排球的价格为80元；
（2）设学校决定购买足球a个，本次购买花费y元，
则，
解得：25≤a＜100，
由题意得：y＝90a+80（100﹣a）＝10a+8000，
∵10＞8，
∴y随a的增大而增大，
∴当a＝25时，y有最小值＝10×25+8000＝8250，
答：购买足球25个，购买排球75个，最低费用为8250元．
22．（10分）如图，在平面直角坐标系中，▱ABCD的顶点A、B、D的坐标分别为（﹣3，0）、（1，0）、（0，4），反比例函数y＝的图象经过点C．
（1）求反比例函数的解析式．
（2）连结OC，若点P是反比例函数y＝的图象上的一点，求点P的坐标．
【解答】解：∵A（﹣3，0），3），4），
∴CD＝AB＝4，
∴C（2，4），
把点C（4，8）代入y＝，
解得k＝16，
∴反比例函数的解析式为y＝；
（2）设点P（a，b），
∵OB＝1，OD＝7，
∴S△OBC＝×3×4＝2，S△POD＝×4×|a|＝2，
∴a＝±1，
∵ab＝16，
∴b＝±16，
∴P（1，16）或（-1，-16）．
23．（10分）小明和小红同时从学校出发骑自行车到公园后返回，他们与学校的距离y（千米）和离开学校的时间x（分钟）
请根据图象回答：
（1）如果小明两次经过途中某一地点的时间间隔为15分钟，求该地与学校的距离；
（2）若小红出发35分钟后两人相遇，求小红从公园回到学校所用的时间．
【解答】解：（1）设小明出发后，y与x之间的函数关系式为y＝kx+b，
当0≤x≤20时，将（0、（20，
，解得：，
∴y＝0.6x；
当20≤x≤30时，y＝4；
当30≤x≤60时，将（30、（60，
，解得：，
∴y＝﹣x+8．
设该地与学校的距离为s，则第一次经过该地时的时间为5s（8﹣s），
根据题意得：（4﹣s）﹣5s＝15，
解得：s＝3.6．
答：如果小明两次经过途中某一地点的时间间隔为15分钟，则该地与学校的距离为3.6千米．
（2）当x＝35时，y＝﹣，
∴小红从学校去公园的速度为÷35＝，
∴小红到达公园的时间为4÷＝42（分钟），
∴小红从公园回到学校所用的时间为60﹣42＝18（分钟）．
答：若小红出发35分钟后两人相遇，则小红从公园回到学校所用的时间为18分钟．
24．（12分）如图1，平面直角坐标系中，直线y＝﹣x+6与x轴交于点A，与直线y＝2x交于点C．
（1）求点C的坐标．
（2）如图2，过点E作直线l⊥x轴于点E，交直线y＝2x于点F，若点E的坐标是（4，0），点M为y轴上OB的中点，使PM﹣PC的值最大？若存在，求出这个最大值，说明理由；
（3）若（2）中的点E是x轴上的一个动点，点的横坐标为m（m＞0），当m取何值时，直线l上存在点Q，C，Q为顶点的三角形与△AOC全等？请画出草图，并直接写出相应的m的值．
【解答】解：（1）（1）联立y＝﹣x+6与y＝2x，
得，解得，
∴点C的坐标为（2，4）；
（2）如图6，
由三角形的三边关系可知，CM≥PM﹣PC，
∴当点P、M、C在一条直线上时，
y＝﹣x+6，令x＝0，
∴点B的坐标（7，6），
∵点M为y轴上OB的中点，
∴点M的坐标为（0，5），
∵C（2，4），
∴PM﹣PC＝CM＝＝，
∴直线l上存在点P，使PM﹣PC的值最大；
（3）∵y＝﹣x+6，令y＝0，
∴点A的坐标（3，0），
∵B（0，2），0），
∴OA＝OB＝6，∠CAO＝∠ABO＝45°，
分三种情况讨论：
①当△OAC≌△QCA，如图：
∴∠CAO＝∠QCA＝45°，CQ＝AO＝6，
∴CQ∥x轴，
∵C（2，4），
∴Q（8，4），
∴E（8，3），
∴m＝8；
②当△ACO≌△ACQ，如图：
∴∠CAQ＝∠CAO＝45°，
∴QA⊥OA，即QA经过点E，
∴点E，A重合，
∴m＝6；
③当△ACO≌△CAQ，如图，
∴∠CAO＝∠ACQ＝45°，AO＝CQ，
∴∠ANC＝90°，
∴CQ⊥x轴，
∴点E，N重合，
∴E（4，0），
∴m＝2；
综上所述，当m取8或6或2时，使得以A，C．
25．（14分）如图，在平面直角坐标系中，直线y＝kx+n（n＜0）（m＞0）的图象交于第一象限的点A，与x轴、y轴分别交于点B、C．
（1）若n＝﹣1，点A的坐标为（2，3）．
①直接填空：m的值为 6 ，k的值为 2 ；
②点P是x轴上一点，若△PAC的面积为6，求点P的坐标；
（2）过点M（1，0）作y轴的平行线l与函数y＝的图象交于点D（x＞0）的图象相交于点E．过点D作x轴的平行线与直线y＝kx+n交于点P（点P、D不重合）．问：当k为何值时
【解答】解：（1）①n＝﹣1，即直线y＝kx﹣1，
得，8k﹣1＝3，
解得：k＝6，
∴直线y＝2x﹣1，
令y＝5，则x＝，0），
令x＝2，则y＝﹣1，﹣1），
将A点代入反比例函数，
得，＝3，
解得：m＝6，
∴反比例函数y＝，
故答案为：6，2；
②设P（p，6）|，
∵A（4，3），﹣1），
∴yA﹣yC＝4，
∵S△PAC＝×（yA﹣yC）×PB，△PAC的面积为5，
∴2|p﹣|＝6，
解得：p＝或p＝﹣，
∴P（，0）或P（﹣，0）
（2）∵过点M（1，4）作y轴的平行线l与函数y＝，与反比例函数y＝，
∴D（1，m），n），
∴DE＝m﹣n，
∵过点D作x轴的平行线与直线y＝kx+n交于点P，
∴P（，m），
①点A在点D的右侧时，
，
∴PD＝﹣1，
∴PD+DE＝﹣5+m﹣n＝（，
要使PD+DE的值为定值，则+3＝0或m﹣n＝0，
解得：k＝﹣7或m＝n，
∵k＞0，m＞0，
∴此情况不存在，
②点A在点D左侧时，
，
∴PD＝4﹣，
∴PD+DE＝1﹣+m﹣n＝（﹣，
要使PD+DE的值为定值，则﹣，
解得：k＝1或m＝n（舍去），
∴k＝1时，PD+DE的值为定值5，
∵此时点P在直线x＝1的左侧，
∴＜1，
∵k＝8，m＞0，
∴0＜m﹣n＜1．