




2024年安徽省合肥市中考二模数学试题(原卷版+解析版)
展开1.数学试卷八大题,共23题,满分150分,考试时间共120分钟.
2.试卷包括“试题卷”和“答题卷”两部分.请务必在“答题卷”上答题,在“试题卷”上答题是无效的.
一、选择题(本大题共10小题,每小题4分,满分40分,每小题都给出、、、四个选项,其中只有一个是符合题目要求的.)
1. 的相反数是( )
A. B. 4C. D.
【答案】B
【解析】
【分析】此题考查的是相反数,掌握其定义是解决此题的关键.
根据相反数的定义:只有符号不同的两个数叫做互为相反数解答即可;
【详解】解:的相反数是4.
故选:B.
2. 下列计算正确的是( )
A. B. C. D.
【答案】C
【解析】
【分析】本题考查合并同类项,同底数幂相除,积的乘方,幂的乘方,熟练掌握相关运算法则是解题的关键.
根据合并同类项法则计算判定A,根据同底数幂相除的法则计算并判定B,根据积的乘方的法则计算并判定C,根据幂的乘方的法则计算并判定D.
【详解】解:A、,故此选项计算错误,不符合题意;
B、,故此选项计算错误,不符合题意;
C、,故此选项计算正确,符合题意;
D、,故此选项计算错误,不符合题意;
故选:C.
3. 2024年合肥市政府工作报告中指出,2023年合肥市先进光伏和新型储能产值达1500亿元,用科学记数法表示1500亿,正确的是( )
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查利用科学记数法表示较大的数的方法,学握科学记数法的表示方法是解答本题的关键,这里还需要注䍐的取值.
科学记数法的表示形式为的形式,其中为整数.理定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
【详解】解:1500亿.
故选:A.
4. 一个几何体由4个相同的小正方体搭成,主视图和俯视图如图所示,则原立体图形可能是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了由三视图还原几何体,根据主视图和俯视图即可得出原立体图形,考查了空间想象能力.
【详解】解:由主视图和俯视图可得原立体图形可能是,
故选:B.
5. 自2016年我国正式实施全面两孩政策以来,合肥市学龄儿童人数逐年增长,某校2021年新生入学人数是600人,2023年新生入学人数达到726人,若设入学人数的年平均增长率为,则以下方程正确的是( )
A. B.
C. D.
【答案】B
【解析】
【分析】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
根据2021年到2023年新生入学人数,即可得出关于的一元二次方程,此题得解.
【详解】解:依题意得:.
故选:B.
6. 将一块直角三角板和一把直尺如图放置,如果,则度数是( )
A. B. C. D.
【答案】C
【解析】
【分析】此题考查了平行线的性质.此题难度不大,解题的关键是准确作出辅助线,掌握两直线平行,同位角相等定理的应用.
首先过点作交于,即可得,然后利用两直线平行,同位角相等,即可求得的度数.
【详解】解:如图,
根据题意得:,,
过点作交于,
∴,
,
,
,
故选:C.
7. 若实数、、满足,且,那么的值是( )
A. B. 0C. 1D. 4
【答案】B
【解析】
【分析】本题考查代数式求值.根据得,代入得,再把代入得,然后把整体代入计算即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
∴,
故选:B.
8. 化学实验室有四种溶液:分别是氢氧化钠溶液,碳酸氢钠溶液,稀盐酸溶液和稀硫酸溶液,从中随机取出两种适量溶液,充分混合,有气体生成的概率是( )
A B. C. D.
【答案】C
【解析】
【分析】:此题考查的是用列表法或树状图法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件,用到的知识点为:概率=所求情况数与总情况数之比.
根据题意列出图表得出所有等可能的情况数,找出符合条件的情况数,然后根据概率公式即可得出答案,
【详解】解:氢氧化钠溶液,碳酸氢钠溶液,稀盐酸溶液和稀硫酸溶液,分别用表示,
画树状图如图:
四种溶液中随机取出两种溶液,共有12种可能,其中两种溶液混合后产生气体的有:()碳酸氢钠溶液和稀盐酸溶液、()碳酸氢钠溶液和稀硫酸溶液4种情况,所以有气体生成的概率是.
故选:C.
9. 如图,已知正方形的边长为4,以为底向外作等腰三角形,连接,点是的中点,连接,并延长分别交于点,交延长线于点,若,则的值为( )
A. B. C. 3D.
【答案】D
【解析】
【分析】过点H作于M,交延长线于N,过点G作于P,先由等腰三角形的性质求得,证明四边形是矩形,得,再证明,得,求得,然后证明,得,求得,从而可求得,最后利用勾股定理可求解 .
【详解】解:过点H作于M,交延长线于N,过点G作于P,如图,
∵正方形的边长为4,
∴,
∵,
∴,
∵是等腰三角形,
∴,
∵
∴
∵,,
∴,
∴四边形是矩形,
∴,
∵点是的中点,
∴,
∵,,
∴,
∴
∴
∴,
∵,,
∴,
∴,
∴,
∴
∴
∴
∵
∴
∴
∴
∴,
故选:D.
【点睛】本题考查正方形的性质,矩形的判定与性质,等腰三角形的性质,相似三角形的判定与性质,勾股定理,正确作出辅助线是解题的关键.
10. 已知反比例函数与一次函数的图象如图所示,则函数的图象可能为( )
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查了一次函数的图象与性质、二次函数的图象与性质、反比例函数的图象与性质,由一次函数与反比例函数图象得出,,从而得出抛物线对称轴为直线,由反比例函数与一次函数的图象的交点的横坐标为得出,再求出对称轴为直线,结合抛物线对称轴的位置即可得出答案.
【详解】解:反比例函数图象在第二、四象限,
,
一次函数交于轴于正半轴,
,
反比例函数与一次函数的图象的交点的横坐标为,
,
,
,
解得:,
,
抛物线开口向下,对称轴为直线,
对称轴为直线,
对称轴在到之间,
函数的图象可能为
故选:A.
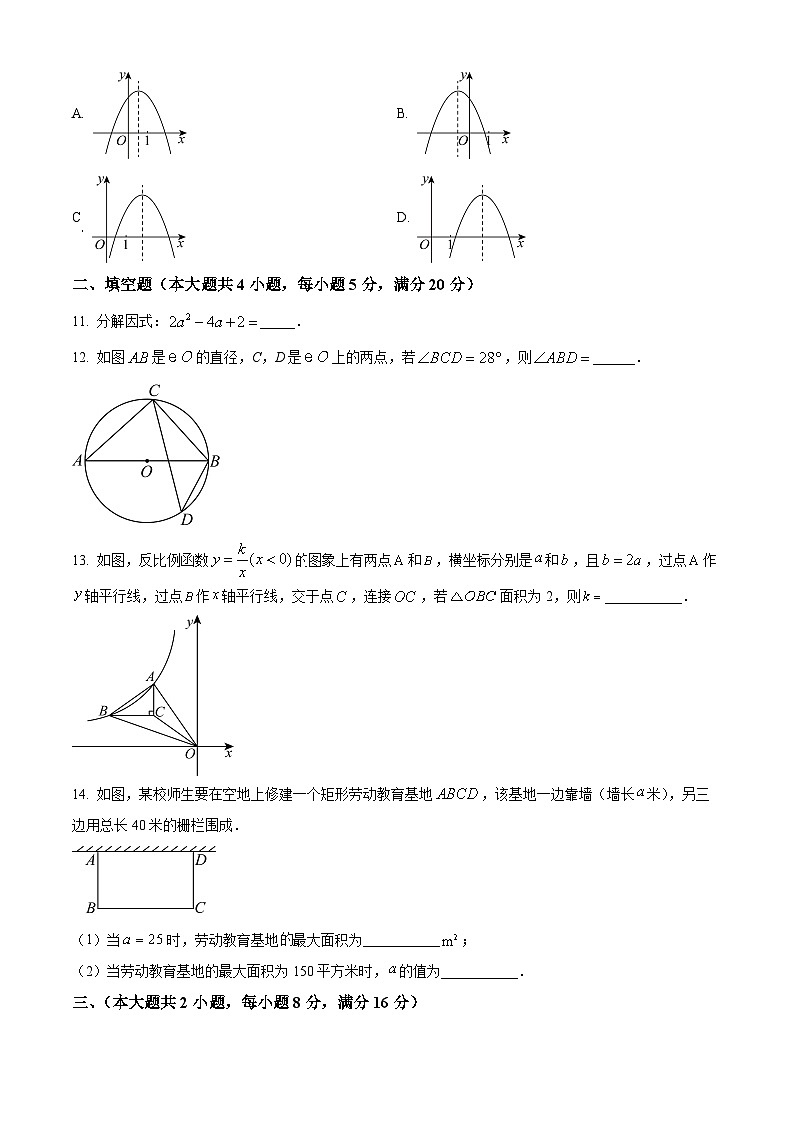
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 分解因式:_____.
【答案】
【解析】
【详解】解:先提取公因式2后继续应用完全平方公式分解即可:
原式,
故答案为:.
12. 如图是直径,C,D是上的两点,若,则______.
【答案】##62度
【解析】
【分析】连接,根据是直径,可知,然后根据同弧所对的圆周角可得,然后根据直角三角形的两锐角互补可得
【详解】连接,则,
∵,
∴.
∵如图是的直径,
∴.
故答案为:.
【点睛】本题考查圆周角定理及推论,直角三角形两锐角互余;由圆周角定理得到相等角是解题的关键.
13. 如图,反比例函数的图象上有两点和,横坐标分别是和,且,过点作轴平行线,过点作轴平行线,交于点,连接,若面积为2,则___________.
【答案】
【解析】
【分析】本题考查了反比例函数与几何综合,根据点和的横坐标分别是和可得,然后根据面积为2列式即可求出k的值.
【详解】解:∵点和的横坐标分别是和,
∴,.
∵面积为2,
∴,
∴,
∵,
∴,
∴.
故答案为:.
14. 如图,某校师生要在空地上修建一个矩形劳动教育基地,该基地一边靠墙(墙长米),另三边用总长40米的栅栏围成.
(1)当时,劳动教育基地的最大面积为___________;
(2)当劳动教育基地的最大面积为150平方米时,的值为___________.
【答案】 ①. ②. 30或10
【解析】
【分析】本题考查二次函数实际应用,实际问题往往是有限制条件的,列出的表达式需考虑自变量的取值范围,运用函数性质解题时更要注意这点.
(1)已知矩形的长和周长可表示宽,运用公式表示面积,根据墙宽得的取值范围;
(2)求当时的值,根据自变量的取值范围回答问题;
【详解】解:(1)当时,另三边总长40米,
设,则,劳动教育基地的面积为y,
根据题意得:,
∴;
∴当时,有最大值,最大值.
(2)当最大值时,即,
∴,
解得:,
∵,
∴或.
故答案为:200;30或10.
三、(本大题共2小题,每小题8分,满分16分)
15. 计算:
【答案】
【解析】
【分析】本题考查了实数的混合运算,解题的关键是掌握实数运算的顺序和相关运算的法则.
先算负整数指数幂,去绝对值,平方根,合并即可;
【详解】
.
16. 如图,在每个小正方形的边长为1个单位的网格中,的顶点均在格点(网格线的交点)上.
(1)将向下平移5个单位得到,画出;
(2)将(1)中的绕点顺时针旋转得到,画出.
【答案】(1)见详解 (2)见详解
【解析】
【分析】本题主要考查了作图-平移变换,旋转变换,熟练掌握平移和旋转的性质是解题的关键.
(1)根据平移的性质画出图形即可;
(2)根据旋转的性质画出图形即可.
【小问1详解】
解:如图,即为所求;
【小问2详解】
如图,即为所求.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,合肥市某画家书画作品装裱前是一个长为米,宽为米的矩形,对此画四周加上宽度相同的边衬进行装裱,装裱后整幅图画长与宽的比是,求边衬的宽度.
【答案】边衬的宽度为米
【解析】
【分析】本题考查分式方程解决实际问题,解答本题的关键是明确题意,列出相应的分式方程.
设边衬的宽度为米,根据题意可知,装䄇后的长为米,宽为米,再根据整幅图画长与宽的比是,即可得到相应的方程进行求解即可.
【详解】解:设边衬的宽度为米,则装裱后的长为米,宽为米,
由题意可得:,
解得:,
经检验,是原分式方程解,
答:边衬的宽度为米.
18. 类比是探索发展的重要途径,是发现新问题、新结论的重要方法.阅读材料:
设的两个根为和,那么比较系数,可得,.
类比推广,回答问题:设的三个根为,,,那么
(___________)(___________).
比较系数,可以得到一元三次方程的根与系数的关系:
___________,___________,___________.
【答案】,,,,,r
【解析】
【分析】本题主要考查根据一元二次方程中根和系数之间的关系推理一元三次方程中根与系数的关系,掌握一元二次方程中根与系数的关系,多项式乘以多项式的运算法则是解题的关键.
将一元三次方程按照一元二次方程的方式因式分解为,再将其按照多项式乘以多项式的方式展开,得到,最后得到根与系数关系,,即可;
【详解】解:根据材料提示得,
,
,
,
,
,
,
,,;
故答案为:,,,,,r.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,已知,以为直径作交于点,过点作的切线交于点,交延长线于点,.
(1)求证:是的中点;
(2)若,,求的半径.
【答案】(1)见详解 (2)
【解析】
【分析】本题考查切线的性质、等腰三角形的性质,圆周角定理,相似三角形的性质和判定,勾股定理等知识,解题的关键是学会添加常用辅助线,利用相似三角形的性质解决问题,属于中考常考题型.
(1)连接,首先证得,证出,即可求解;
(2)连接,根据圆周角定理得出,证明,得出,设的半径为,再根据勾股定理得出,列出方程即可求解;
【小问1详解】
解:连接,如图,
∵是的切线,,
∴,
∴,
∴,
∴,
∴,
∴是的中点;
【小问2详解】
连接,如图,
∵是的直径;
∴,
,
∴,
,
∴,
∴,
∴,
∴,
∴,
设的半径为,
,
,
∴,
解得:或(舍去).
故半径为.
20. 如图①为我们常见的马扎,马扎上层是可以折叠但不能伸缩的帆布,图②是马扎撑开后的侧面示意图,其中腿和的长度相等,是它们的中点,,,当有人坐在马扎上时,马扎侧面示意图变成图③(假设与都是线段),且,点离地面的距离即马扎实际支撑的高度.若某人坐在马扎上时测得,他要求实际支撑高度为,请问这款马扎能否符合他的要求?(参考数据:,,)
【答案】这款马扎不能符合他的要求
【解析】
【分析】本题考查了解直角三角形的应用,三角函数的定义,正确地作出辅助线是解题的关键.
连接,过作的垂线交于,交于,根据题意可得,,, ,根据等腰三角形的性质得出,证明,从而得出,算出,,再根据勾股定理算出,从而算出,即可求解;
【详解】解:连接,过作的垂线交于,交于,
根据题意可得,.,,
∴是的垂直平分线,
∵,
∴点E在上,
,
,
,
,
,
,
,
,
故这款马扎不能符合他的要求.
21. 某校为了落实“双减”工作,丰富学生的课外生活,开展“雅言颂经典,真情咏中华”经典诵读活动.为了了解学生的参与度,从学校随机抽取了一部分学生进行调查,表示每天诵读时长,把调查学生的诵读时长分为5个等级,每个等级的范围如下表所示,并绘制了条形统计图和扇形统计图.
请根据图表中的信息,解答下列问题:
(1)补全条形统计图;
(2)求出扇形统计图中等级的圆心角度数;
(3)学校为了鼓励学生积极参加该项活动,准备给诵读时长不低于20分钟的同学给予“诵读之星”称号,该校共有2000名学生,请问获得“诵读之星”称号的学生约有多少人?
【答案】(1)见解析 (2)
(3)1300人
【解析】
【分析】本题考查条形统计图、用样本估计总体、扇形统计图,解题的关键是明确题意,找出所求问题需要的条件.
(1)根据等级人数及其百分比可得总人数;总人数乘以等级百分比可得其人数,即可补全条形统计图;
(2)先求出“”等级对应的人数,用乘以“”等级的百分比即可;
(3)总人数乘以样本中等级学生的百分比之和即可求解.
【小问1详解】
本次共抽查学生(人,
条形图中“”等级对应的人数为(人,补全图形如下:
【小问2详解】
“”等级对应的人数为(人),
“”等级所在扇形的圆心角度数为.
【小问3详解】
(人,
答:获得“诵读之星”称号的学生约有1300人,
22. 如图,二次函数的图象过,,三点,点是二次函数图象上一点,点的横坐标是,直线与轴交于点,且.
(1)求二次函数的表达式;
(2)过点,作直线于点,作轴于点,并交于点.
①当时,求的长;
②是否存在点,使最大?若存在,求出点坐标,若不存在,请说明理由.
【答案】(1)
(2)①;②当时,最大,此时点坐标为
【解析】
【分析】(1)将点代入中得到关于的方程组,解方程组求出即可得到二次函数的表达式;
(2)先求出直线的解析式为,设点表示出;①直接代入求解即可;②表示出,据此可得出关于的函数关系式,然后根据函数的最大值即可求出点的坐标;
【小问1详解】
将点代入,
得:,
解得:,
∴二次函数的表达式为:;
【小问2详解】
设直线的解析式为:,
将代入
得:,
解得:
∴直线的解析式为:,
∵点的横坐标是,直线与轴交于点,
∴,
则,,
①当时,;
②根据题意得,
∴,
∴,
故当时,最大,此时点坐标为.
【点睛】此题主要考查了求函数解析式,二次函数的最值,函数的交点坐标等,解答此题的关键是熟练掌握待定系数法求二次函数、一次函数的解析式,以及求函数交点坐标的方法,难点是方程思想在解题中的应用,漏解是解答此题的易错点之一.
23. 已知矩形,,,把矩形绕点顺时针旋转,得到矩形,连接,交于点.
(1)如图1,若点落在边上,过点作,垂足为点,连接,求证:;
(2)如图2,若点在上方,连接交于点,连接,若,
①求证:;
②求的长.
【答案】(1)证明见解析
(2)①证明见解析;②
【解析】
【分析】(1)先由旋转的性质得到,,则,再由矩形的性质得到,,进而证明,则由角平分线的性质可得,进而得到,据即可利用
(2)①如图所示,过点B作于H,证明,推出,由旋转的性质可得,则,可得或(舍去),则;再证明,得到;设,则,由勾股定理得,解得或(舍去);则,即可由相似三角形的性质得到;②同理可证明,进而证明,则,求出,,则.
【小问1详解】
证明:由旋转的性质可得,,
∴,
∵四边形是矩形,
∴,,
∴,
∴,
∵,
∴,
∴,
∵四边形是矩形,
∴,
又∵,
∴;
【小问2详解】
解:①如图所示,过点B作于H,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∴,
∴,即,
∵,,
∴由旋转的性质可得,
∴,
∴或(舍去),
∴;
∵,
∴,
∴,
∴;
设,则,
在中,由勾股定理得,
∴,
解得或(舍去);
∴,
∵,
∴;
②由旋转的性质可得,
∴,
∵四边形是矩形,
∴,,
∴,
∴,
又∵,
∴,
∴,
∵,,
∴.
【点睛】本题主要考查了矩形的性质,旋转的性质,相似三角形的性质与判定,勾股定理,全等三角形的性质与判定,等边对等角等等,正确作出辅助线构造相似三角形是解题的关键.等级
时长范围(分钟)
2024年安徽省合肥市肥东县中考二模数学试题(原卷版+解析版): 这是一份2024年安徽省合肥市肥东县中考二模数学试题(原卷版+解析版),文件包含2024年安徽省合肥市肥东县中考二模数学试题原卷版docx、2024年安徽省合肥市肥东县中考二模数学试题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
2024年安徽省蚌埠市中考二模数学试题(原卷版+解析版): 这是一份2024年安徽省蚌埠市中考二模数学试题(原卷版+解析版),文件包含2024年安徽省蚌埠市中考二模数学试题原卷版docx、2024年安徽省蚌埠市中考二模数学试题解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
2024年安徽省合肥市庐阳区第四十二中学中考一模数学试题(原卷版+解析版): 这是一份2024年安徽省合肥市庐阳区第四十二中学中考一模数学试题(原卷版+解析版),文件包含2024年安徽省合肥市庐阳区第四十二中学中考一模数学试题原卷版docx、2024年安徽省合肥市庐阳区第四十二中学中考一模数学试题解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。












