




专题02 函数及其性质(24题型)(讲练)-2024年中考数学二轮复习讲义(全国通用)
展开一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准,安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
专题02 函数及其性质
目 录
TOC \ "1-3" \n \h \z \u \l "_Tc160094594" 一、考情分析
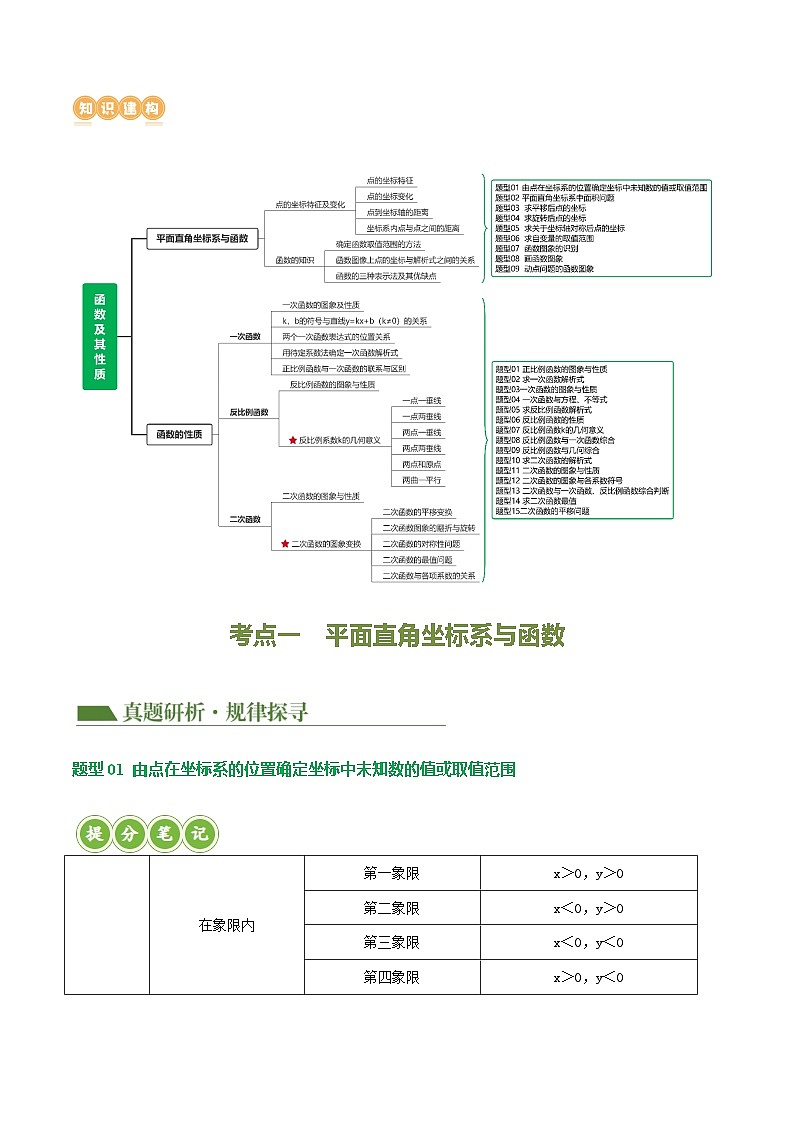
二、知识建构
\l "_Tc160831023" 考点一 平面直角坐标系与函数
\l "_Tc160831024" \l "_Tc160094596" \l "_Tc160094596" 【真题研析·规律探寻】
\l "_Tc160831025" 题型01 由点在坐标系的位置确定坐标中未知数的值或取值范围
\l "_Tc160831026" 题型02 平面直角坐标系中面积问题
\l "_Tc160831027" 题型03 求平移后点的坐标
\l "_Tc160831028" 题型04 求旋转后点的坐标
\l "_Tc160831029" 题型05 求关于坐标轴对称后点的坐标
\l "_Tc160831030" 题型06 求自变量的取值范
\l "_Tc160831031" 题型07 函数图象的识别
\l "_Tc160831032" 题型08 画函数图象
\l "_Tc160831033" 题型09 动点问题的函数图象
\l "_Tc160094604" 【核心提炼·查漏补缺】
\l "_Tc160094605" 【好题必刷·强化落实】
\l "_Tc160831036" 考点二 一次函数、反比例函数、二次函数的性质
\l "_Tc160831037" \l "_Tc160094596" \l "_Tc160094596" 【真题研析·规律探寻】
\l "_Tc160831038" 题型01 正比例函数的图象与性质
\l "_Tc160831039" 题型02 求一次函数解析式
\l "_Tc160831040" 题型03一次函数的图象与性质
\l "_Tc160831041" 题型04 一次函数与方程、不等式
\l "_Tc160831042" 题型05 求反比例函数解析式
\l "_Tc160831043" 题型06 反比例函数的性质
\l "_Tc160831044" 题型07 反比例函数k的几何意义
\l "_Tc160831045" 题型08 反比例函数与一次函数综合
\l "_Tc160831046" 题型09 反比例函数与几何综合
\l "_Tc160831047" 题型10 求二次函数的解析式
\l "_Tc160831048" 题型11 二次函数的图象与性质
\l "_Tc160831049" 题型12 二次函数的图象与各系数符号
\l "_Tc160831050" 题型13 二次函数与一次函数、反比例函数综合判断
\l "_Tc160831051" 题型14 求二次函数最值
\l "_Tc160831052" 题型15 二次函数的平移问题
\l "_Tc160094604" 【核心提炼·查漏补缺】
\l "_Tc160094605" 【好题必刷·强化落实】
考点一 平面直角坐标系与函数
题型01 由点在坐标系的位置确定坐标中未知数的值或取值范围
1.(2023·山东日照·统考中考真题)若点Mm+3,m−1在第四象限,则m的取值范围是 .
【答案】−3
【分析】根据第四象限的点横坐标为正,纵坐标为负进行求解即可.
【详解】解:∵点Mm+3,m−1在第四象限,
∴m+3>0m−1<0,
解得−3
2.(2023·广东湛江·统考二模)已知点P(−12,2a+6)在x轴上,则a的值为 .
【答案】−3
【分析】本题考查了x轴上的点的坐标特征,熟记x轴上点的纵坐标为0是解题的关键.根据x轴上点的纵坐标为0列方程求出a即可.
【详解】解:∵P(−12,2a+6)在x轴上,
∴2a+6=0,
解得a=−3,
故答案为:−3.
3.(2023·四川巴中·统考中考真题)已知a为正整数,点P(4,2−a)在第一象限中,则a= .
【答案】1
【分析】根据点在第一象限,则2−a>0,根据a为正整数,则a>0,即可.
【详解】∵点P(4,2−a)在第一象限中,
∴2−a>0,
∴a<2,
∵a为正整数,
∴a>0,
∴0
故答案为:1
【点睛】本题考查平面直角坐标系的知识,解题的关键是掌握点的坐标的性质.
题型02 平面直角坐标系中面积问题
关于平面直角坐标系中面积问题,常见的4种类型:
1)直接利用面积公式求面积.(特征:当三角形的一边在x轴或y轴上时,常用这种方法.)
【方法技巧】在求几何图形面积时,线段的长度往往通过计算某些点横坐标之差的绝对值,或纵坐标之差的绝对值去实现. (横坐标相减时最好用右边的数减左边的数,纵坐标相减时用上边的数减下边的数,这样所得结果就是边或高的长度,就不用绝对值符号了).
2)已知三角形面积求点的坐标.
【方法技巧】已知面积求点的坐标时,应先画出图形,再看图形的面积跟哪些线段有关系,当用坐标表示线段长度时,应取坐标的绝对值.
3)利用补形法求面积. (当所求图形的边都不在x轴或y轴上时,一般用该方法.)
【出题类型】求网格中的多边形面积.
4)利用割补法求面积.(特征:将不规则图形分割为规则图形计算面积,可根据题的特点灵活选择解法.)
【出题类型】与二次函数有关的面积问题.
【方法技巧】用铅垂定理巧求斜三角形面积的计算公式:三角形面积等于水平宽和铅锤高乘积的一半.
1.(2023·广西柳州·统考三模)如图,已知△ABC的顶点分别为A(−2,2),B(−4,5),C(−5,1).
(1)作出△ABC关于x轴对称的图形△A1B1C1.
(2)点P在x轴上运动,当AP+CP的值最小时,求出点P的坐标.
(3)求△ABC的面积.
【答案】(1)见解析
(2)P−4,0
(3)5.5
【分析】(1)分别作三个顶点的关于x轴的对称点,再依次连接即可;
(2)先确定点P,再根据待定系数法求出直线CA1的关系式,然后令y=0,可得答案;
(3)根据矩形的面积−3个三角形的面积,即可求出答案.
【详解】(1)如图所示.
(2)根据对称性可知AP=A1P,
∴AP+CP=A1P+CP,
根据两点之间线段最短,可知连接CA1,与x轴相交于点P,点P即为所求.
设直线CA1的函数解析式为:y=kx+b(k≠0).
把C(−5,1),A(−2,−2)代入得:−5k+b=1−2k+b=−2,
解得:k=−1b=−4,
∴直线CA1的函数解析式为:y=−x−4,
把y=0代入得:−x−4=0,解得:x=−4,
∴P(−4,0).
(3)S△ABC=3×4−12×1×3−12×2×3−12×1×4=5.5.
【点睛】本题主要考查了作轴对称图形,求线段和最小,求三角形的面积等,根据线段的性质确定点P的位置是解题的关键.
2.(2023·陕西铜川·统考三模)如图,抛物线y=ax2+3x+ca≠0与x轴交于点A−2,0和点B,与y轴交于点C0,8,顶点为D,连接AC,CD,DB,直线BC与抛物线的对称轴l交于点E.
(1)求抛物线的解析式和直线BC的解析式;
(2)求四边形ABDC的面积;
(3)P是第一象限内抛物线上的动点,连接PB,PC,当S△PBC=35S△ABC时,求点P的坐标.
【答案】(1)y=−12x2+3x+8,y=−x+8
(2)70
(3)点P的坐标为2,12或P6,8
【分析】(1)根据待定系数法求二次函数解析式,然后令y=0,求得B点的坐标,进而求得BC的解析式;
(2)设抛物线的对称轴l与x轴交于点H,根据解析式得出顶点D的坐标为(3,252),进而根据S四边形ABDC=S△AOC+S梯形OCDH+S△BDH即可求解;
(3)依题意得出S△PBC=35S△ABC=24,过点P作PG⊥x轴,交x轴于点G,交BC于点F.设点P(t,−12t2+3t+8),F(t,−t+8),则PF=−12t2+4t,进而根据三角形面积公式建立方程,解方程即可求解.
【详解】(1)解:∵抛物线y=ax2+3x+c(a≠0)过点A−2,0和C(0,8),
∴4a−6+c=0c=8,
解得a=−12c=8,
∴抛物线的解析式为y=−12x2+3x+8,
令y=0,得−12x2+3x+8=0,
解得x1=−2,x2=8,
∴点B的坐标为(8,0),
设直线BC的解析式为y=kx+b,
把点B(8,0),C(0,8)分别代入y=kx+b,
得6k+b=0b=8,
解得k=−1b=8,
∴直线BC的解析式为y=−x+8;
(2)如图1,设抛物线的对称轴l与x轴交于点H,
∵抛物线的解析式为y=−12x2+3x+8=−12(x−3)2+252,
∴顶点D的坐标为(3,252),
∴S四边形ABDC=S△AOC+S梯形OCDH+S△BDH
=12AO⋅OC+12(OC+DH)⋅OH+12HB⋅HD
=12×2×8+12×(8+252)×3+12×5×252
=70;
(3)∵S△ABC=12AB⋅OC=12×10×8=40,
∴S△PBC=35S△ABC=24,
如图2,过点P作PG⊥x轴,交x轴于点G,交BC于点F.
设点P(t,−12t2+3t+8),
∵点F在直线BC上,
∴F(t,−t+8),
∴PF=−12t2+4t,
∴S△PBC=12PF⋅(OG+GB)=12PF⋅OB=24,
∴12(−12t2+4t)×8=24,
解得t1=2,t2=6,
∴点P的坐标为2,12或P6,8.
【点睛】本题考查了二次函数综合,待定系数法求二次函数解析式,面积问题,熟练掌握二次函数的性质是解题的关键.
3.如图在平面直角坐标系中,已知Aa,0,Bb,0,M−1.5,−2,其中a、b满足a+1+b−32=0.
(1)求△ABM的面积;
(2)在x轴上求一点P,使得△AMP的面积与△ABM的面积相等;
(3)在y轴上存在使△BMP的面积与△ABM的面积相等的P点,请直接写出点P的坐标.
【答案】(1)S△ABM=4;
(2)P−5,0;
(3)点P的坐标为0,49或0,−289.
【分析】(1)先根据非负性的性质求出a、b的值,再根据三角形面积公式求解即可;
(2)设点Pp,0,根据三角形面积公式进行求解即可得到答案;
(3)设BM交y轴于点D,设P(0,q),D0,d,先利用面积法求出d=−43.则D0,−43,再根据S△ABM=S△BMP,得到12×|q−−43|×3−−1.5=4,由此即可得到答案.
【详解】(1)解:∵a+1+b−32=0,且|a+1|≥0,b−32≥0,
∴a+1=0,b−3=0,
∴a=−1,b=3,
∴A−1,0,B3,0,
∴S△ABM=12AB⋅yM=12×4×2=4;
(2)解:设点Pp,0.
由题意得S△AMP=12×−1−p×2=4,
∴p=3或p=−5.
当p=3时,△AMP与△ABM重合,不合题意,舍去,
∴点P−5,0;
(3)解:如图②,设BM交y轴于点D,设P(0,q),D0,d.
∵S△BOM=12OD⋅(xB−xM)=12OB⋅−yC=12×3×2=12×3−−1.5×(−d)=3,
∴d=−43.
∴D0,−43.
∵S△ABM=S△BMP,
∴12PD⋅(xB−xM)=4,
∴12×|q−−43|×3−−1.5=4,
解得q=49或−289.
∴点P的坐标为0,49或0,−289.
【点睛】本题主要考查了坐标与图形,三角形面积,绝对值方程,非负数的性质,解题的关在于能够熟练掌握非负数的性质,求出a、b的值.
4.【知识呈现】
当三角形的三边都不与坐标轴平行时,对于三角形的面积因不易求出底边和高的长度,所以不能直接利用三角形的面积公式来求,但可以将不规则图形运用补法或割法转化成规则的图形(如长方形,梯形),再运用和、差关系进行求解.
【问题解答】
在平面直角坐标系中,△ABC三个顶点的坐标分别为A−1,3,B−3,−1,C2,1.
(1)如图1,分别以点A,B,C向坐标轴作垂线构造长方形BDEF,求△ABC的面积;
(2)在图1中过点A作AG∥y轴交BC于点G,如图2.
①求AG的长;
②猜想:△ABC的面积S与DE·AG的数量关系式为______.
【答案】(1)8
(2)①3.2 ②S=DE·AG2
【分析】(1)根据S△ABC=S矩形BDEF−S△ABD−S△ACE−S△BCF即可求得答案.
(2)①根据S△ABC=S△ABG+S△ACG=12×2×AG+12×3×AG=8即可求得答案.②根据S△ABC=S△ABG+S△ACG=12×2×AG+12×3×AG=12×5AG,DE=5即可求得答案.
【详解】(1)S△ABC=S矩形BDEF−S△ABD−S△ACE−S△BCF=20−4−3−5=8.
(2)①根据题意可得
S△ABC=S△ABG+S△ACG=12×2×AG+12×3×AG=8.
解得
AG=3.2.
②因为S△ABC=S△ABG+S△ACG=12×2×AG+12×3×AG=12×5AG,DE=5,可得
S△ABC=DE·AG2,即S=DE·AG2.
故答案为:S=DE·AG2.
【点睛】本题主要考查平面直角坐标系与几何图形,能采用补法和割法求图形面积是解题的关键.
5.对于某些三角形或四边形,我们可以直接用面积公式或者用割补法来求它们的面积.下面我们再研究一种求某些三角形或四边形面积的新方法:
如图1,2所示,分别过三角形或四边形的顶点A,C作水平线的铅垂线l1,l2,l1,l2之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交AC于点D,称线段BD的长叫做这个三角形的铅垂高;如图2所示,分别过四边形的顶点B,D作水平线l3,l4,l3,l4之间的距离ℎ叫做四边形的铅垂高.
【结论提炼】
容易证明:“三角形的面积等于水平宽与铅垂高乘积的一半”,即“S=12dℎ”
【结论应用】
为了便于计算水平宽和铅垂高,我们不妨借助平面直角坐标系.
已知:如图3,点A−5,2,B5,0,C0,5,则△ABC的水平宽为10,铅垂高为______,所以△ABC面积的大小为______.
【再探新知】
三角形的面积可以用“水平宽与铅垂高乘积的一半”来求,那四边形的面积是不是也可以这样求呢?带着这个问题,我们进行如下探索:
(1)在图4所示的平面直角坐标系中,取A−4,2,B1,5,C4,1,D−2,−4四个点,得到四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是______;用其它的方法进行计算得到其面积的大小是______,由此发现:用“S=12dℎ”这一方法对求图4中四边形的面积______.(填“适合”或“不适合”)
(2)在图5所示的平面直角坐标系中,取A−5,2,B1,5,C4,2,D−2,−3四个点,得到了四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是______,用其它的方法进行计算得到面积的大小是______,由此发现:用“S=12dℎ”这一方法对求图5中四边形的面积______.(“适合”或“不适合”)
(3)在图6所示的平面直角坐标系中,取A−4,2,B1,5,C5,1,D−1,−5四个点,得到了四边形ABCD.通过计算发现:用“S=12dℎ”这一方法对求图6中四边形的面积______.(填“适合”或“不适合”)
【归纳总结】
我们经历上面的探索过程,通过猜想、归纳,验证,便可得到:当四边形满足某些条件时,可以用“S=12dℎ”来求面积.那么,可以用“S=12dℎ”来求面积的四边形应满足的条件是:______.
【答案】结论应用:4,20;
再探新知:(1)36,37.5,不合适;
(2)36,36,合适;
(3)合适;
归纳总结:一条对角线等于水平宽或铅垂高.
【分析】结论应用:直接代入公式即可;
再探新知:(1)求出水平宽,铅垂高,代入公式求出面积,再利用矩形面积减去周围四个三角形面积可得答案;
(2)(3)与(1)同理;
归纳总结:当四边形满足一条对角线等于水平宽或铅垂高时,四边形可以用“S=12dh”来求面积.
【详解】解:结论应用:由图形知,铅垂高为4,S△ABC=12×10×4=20,
故答案为:4,20;
再探新知:
(1)∵四边形ABCD的水平宽为8,铅垂高为9,
∴运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小为36,
利用四边形ABCD所在的矩形面积减去周围四个三角形面积为:
8×9-12×2×6−12×3×5−12×6×5−12×3×4=37.5,
∴用“S=12dh”这一方法对求图4中四边形的面积不合适,
故答案为:36,37.5,不合适;
(2)∵四边形ABCD的水平宽为9,铅垂高为8,
∴运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小为36,
利用四边形ABCD所在的矩形面积减去周围四个三角形面积为:
8×9-12×3×5−12×6×5−12×3×6−12×3×3=36,
∴用“S=12dh”这一方法对求图4中四边形的面积,合适,
故答案为:36,36,合适;
(3)∵四边形ABCD的水平宽为9,铅垂高为10,
∴运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小
45,
利用四边形ABCD所在的矩形面积减去周围四个三角形面积为:
10×9-12×5×7−12×4×6−12×5×3−12×4×4=45,
∴用“S=12dh”这一方法对求图4中四边形的面积,合适,
故答案为:合适;
归纳总结:当四边形满足一条对角线等于水平宽或铅垂高时,四边形可以用“S=12dh”来求面积,
故答案为:一条对角线等于水平宽或铅垂高.
【点睛】本题主要考查了图形的面积,坐标与图形,割补法求不规则图形的面积等知识,由特殊到一般,采用类比的方法是解题的关键.
题型03 求平移后点的坐标
1.(2022·广东·统考中考真题)在平面直角坐标系中,将点1,1向右平移2个单位后,得到的点的坐标是( )
A.3,1B.−1,1C.1,3D.1,−1
【答案】A
【分析】把点1,1的横坐标加2,纵坐标不变,得到3,1,就是平移后的对应点的坐标.
【详解】解:点1,1向右平移2个单位长度后得到的点的坐标为3,1.
故选:A.
【点睛】本题考查了坐标与图形变化﹣平移.掌握平移的规律是解答本题的关键.
2.(2022·海南·统考中考真题)如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(7,2)B.(7,5)C.(5,6)D.(6,5)
【答案】D
【分析】先过点C做出x轴垂线段CE,根据相似三角形找出点C的坐标,再根据平移的性质计算出对应D点的坐标.
【详解】
如图过点C作x轴垂线,垂足为点E,
∵∠ABC=90°
∴∠ABO+∠CBE=90°
∵∠CBE+BCE=90°
∴∠ABO=∠BCE
在ΔABO和ΔBCE中,
{∠ABO=∠BCE∠AOB=∠BEC=90° ,
∴ΔABO∽ΔBCE,
∴ABBC=AOBE=OBEC=12 ,
则BE=2AO=6 ,EC=2OB=2
∵点C是由点B向右平移6个单位,向上平移2个单位得到,
∴点D同样是由点A向右平移6个单位,向上平移2个单位得到,
∵点A坐标为(0,3),
∴点D坐标为(6,5),选项D符合题意,
故答案选D
【点睛】本题考查了图象的平移、相似三角形的判定与性质,利用相似三角形的判定与性质找出图象左右、上下平移的距离是解题的关键.
3.(2021·浙江丽水·统考中考真题)四盏灯笼的位置如图.已知A,B,C,D的坐标分别是 (−1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )
A.将B向左平移4.5个单位B.将C向左平移4个单位
C.将D向左平移5.5个单位D.将C向左平移3.5个单位
【答案】C
【分析】直接利用利用关于y轴对称点的性质得出答案.
【详解】解:∵点A (−1,b) 关于y轴对称点为B (1,b),
C (2,b)关于y轴对称点为(-2,b),
需要将点D (3.5,b) 向左平移3.5+2=5.5个单位,
故选:C.
【点睛】本题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.(2022·山东淄博·统考中考真题)如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是 .
【答案】(1,3)
【分析】根据点A和点A1的坐标可得出平移规律,从而进一步可得出结论.
【详解】解:∵顶点A(﹣3,4)的对应点是A1(2,5),
又−3+5=2,4+1=5
∴平移ΔABC至ΔA1B1C1的规律为:将ΔABC向右平移5个单位,再向上平移1个单位即可得到ΔA1B1C1
∵B(﹣4,2)
∴B1的坐标是(-4+5,2+1),即(1,3)
故答案为:(1,3)
【点睛】本题主要考查了坐标与图形,正确找出平移规律是解答本题的关键.
题型04 求旋转后点的坐标
1.(2021·黑龙江牡丹江·统考中考真题)如图,△AOB中,OA=4,OB=6,AB=27,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(4,2)或(﹣4,2)B.(23,﹣4)或(﹣23,4)
C.(﹣23,2)或(23,﹣2)D.(2,﹣23)或(﹣2,23)
【答案】C
【分析】先求出点A的坐标,再根据旋转变换中,坐标的变换特征求解;或根据题意画出图形旋转后的位置,根据旋转的性质确定对应点A′的坐标.
【详解】过点A作AC⊥OB于点C.
在Rt△AOC中,AC2=OA2−OC2 .
在Rt△ABC中,AC2=AB2−CB2=AB2−OB−OC2 .
∴ OA2−OC2=AB2−OB−OC2.
∵OA=4,OB=6,AB=27,
∴OC=2.
∴AC=23.
∴点A的坐标是2,23.
根据题意画出图形旋转后的位置,如图,
∴将△AOB绕原点O顺时针旋转90°时,点A的对应点A′的坐标为23,−2;
将△AOB绕原点O逆时针旋转90°时,点A的对应点A′′的坐标为−23,2.
故选:C.
【点睛】本题考查了解直角三角形、旋转中点的坐标变换特征及旋转的性质.(a,b)绕原点顺时针旋转90°得到的坐标为(b,-a),绕原点逆时针旋转90°得到的坐标为(-b,a).
2.(2022·山东枣庄·统考中考真题)如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
A.(4,0)B.(2,﹣2)C.(4,﹣1)D.(2,﹣3)
【答案】C
【分析】根据平移和旋转的性质,将△ABC先向右平移1个单位,再绕P点顺时针方向旋转90°,得到△A′B′C′,即可得点B的对应点B'的坐标.
【详解】作出旋转后的图形如下:
∴B'点的坐标为(4,﹣1),
故选:C.
【点睛】本题考查了坐标与图形变换−旋转、平移,解决本题的关键是掌握旋转的性质.
3.(2022·山东青岛·统考中考真题)如图,将△ABC先向右平移3个单位,再绕原点O旋转180°,得到△A'B'C',则点A的对应点A'的坐标是( )
A.(2,0)B.(−2,−3)C.(−1,−3)D.(−3,−1)
【答案】C
【分析】先画出平移后的图形,再利用旋转的性质画出旋转后的图形即可求解.
【详解】解:先画出△ABC平移后的△DEF,再利用旋转得到△A'B'C',
由图像可知A'(-1,-3),
故选:C.
【点睛】本题考查了图形的平移和旋转,解题关键是掌握绕原点旋转的图形的坐标特点,即对应点的横纵坐标都互为相反数.
4.(2022·湖南湘潭·统考中考真题)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A−1,1,B−4,0,C−2,2.将△ABC绕原点O顺时针旋转90°后得到△A1B1C1.
(1)请写出A1、B1、C1三点的坐标:A1_________,B1_________,C1_________
(2)求点B旋转到点B1的弧长.
【答案】(1)(1,1);(0,4);(2,2)
(2)2π
【分析】(1)将△ABC绕着点O按顺时针方向旋转90°得到△A1B1C1,点A1,B1,C1的坐标即为点A,B,C绕着点O按顺时针方向旋转90°得到的点,由此可得出结果.
(2)由图知点B旋转到点B1的弧长所对的圆心角是90º,OB=4,根据弧长公式即可计算求出.
【详解】(1)解:将△ABC绕着点O按顺时针方向旋转90°得到△A1B1C1,点A1,B1,C1的坐标即为点A,B,C绕着点O按顺时针方向旋转90°得到的点,
所以A1(1,1);B1(0,4);C1(2,2)
(2)解:由图知点B旋转到点B1的弧长所对的圆心角是90度,OB=4,
∴点B旋转到点B1的弧长=90180×π×4=2π
【点睛】本题主要考查点的旋转变换和弧长公式,解题的关键是熟练掌握旋转变换的定义和弧长公式.
题型05 求关于坐标轴对称后点的坐标
1.(2022·江苏常州·统考中考真题)在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是( )
A.(−2,1)B.(−2,−1)C.(−1,2)D.(−1,−2)
【答案】D
【分析】直接利用关于x,y轴对称点的性质分别得出A,A2点坐标,即可得出答案.
【详解】解:∵点A1的坐标为(1,2),点A与点A1关于x轴对称,
∴点A的坐标为(1,-2),
∵点A与点A2关于y轴对称,
∴点A2的坐标是(-1,﹣2).
故选:D.
【点睛】此题主要考查了关于x,y轴对称点的坐标,正确掌握关于坐标轴对称点的性质是解题关键.
2.(2023·浙江金华·统考中考真题)如图,两个灯笼的位置A,B的坐标分别是−3,3,1,2,将点B向右平移2个单位,再向上平移1个单位得到点B',则关于点A,B'的位置描述正确是( )
A.关于x轴对称B.关于y轴对称
C.关于原点O对称D.关于直线y=x对称
【答案】B
【分析】先根据平移方式求出B'3,3,再根据关于y轴对称的点横坐标互为相反数,纵坐标相同进行求解即可.
【详解】解:∵将B1,2向右平移2个单位,再向上平移1个单位得到点B',
∴B'3,3,
∵A−3,3,
∴点A,B'关于y轴对称,
故选B.
【点睛】本题主要考查了坐标与图形变化—平移和轴对称,正确根据平移方式求出B'3,3是解题的关键.
3.(2022·广西贵港·中考真题)若点A(a,−1)与点B(2,b)关于y轴对称,则a−b的值是( )
A.−1B.−3C.1D.2
【答案】A
【分析】根据关于y轴对称的点,纵坐标相同,横坐标互为相反数解答即可.
【详解】∵点A(a,−1)与点B(2,b)关于y轴对称,
∴a=-2,b=-1,
∴a-b=-1,
故选A.
【点睛】本题考查了关于y轴对称的点坐标的关系,代数式求值,解题的关键在于明确关于y轴对称的点纵坐标相等,横坐标互为相反数.
题型06 求自变量的取值范
函数有意义时字母的取值范围一般从几个方面考虑:
①当函数解析式是整式时,字母可取全体实数;
②当函数解析式是分式时,考虑分式的分母不能为0;
③当函数解析式是二次根式时,被开方数为非负数.
注意:实际问题中函数取值范围要和实际情况相符合,使之有意义.
1.(2020·湖北黄石·中考真题)函数y=1x−3+x−2的自变量x的取值范围是( )
A.x≥2,且x≠3B.x≥2C.x≠3D.x>2,且x≠3
【答案】A
【分析】根据分式与二次根式的性质即可求解.
【详解】依题意可得x-3≠0,x-2≥0
解得x≥2,且x≠3
故选A.
【点睛】此题主要考查函数的自变量取值,解题的关键是熟知分式与二次根式的性质.
2.(2022·湖北恩施·统考中考真题)函数y=x+1x−3的自变量x的取值范围是( )
A.x≠3B.x≥3
C.x≥−1且x≠3D.x≥−1
【答案】C
【分析】根据分式有意义的条件与二次根式有意义的条件得出不等式组,解不等式组即可求解.
【详解】解:∵x+1x−3有意义,
∴x+1≥0,x−3≠0,
解得x≥−1且x≠3,
故选C.
【点睛】本题考查了求函数自变量的取值范围,掌握分式有意义的条件与二次根式有意义的条件是解题的关键.
3.(2022·湖南娄底·统考中考真题)函数y=1x−1的自变量x的取值范围是 .
【答案】x>1
【分析】由1x−1有意义可得:x−1>0,再解不等式可得答案.
【详解】解:由1x−1有意义可得:
{x−1≥0x−1≠0, 即x−1>0,
解得:x>1.
故答案为:x>1
【点睛】本题考查的是二次根式与分式有意义的条件,函数自变量的取值范围,理解函数自变量的取值范围的含义是解本题的关键.
题型07 函数图象的识别
1.(2023·浙江绍兴·统考中考真题)已知点M−4,a−2,N−2,a,P2,a在同一个函数图象上,则这个函数图象可能是( )
A. B. C. D.
【答案】B
【分析】点M−4,a−2,N−2,a,P2,a在同一个函数图象上,可得N、P关于y轴对称,当x<0时,y随x的增大而增大,即可得出答案.
【详解】解:∵N−2,a,P2,a,
∴得N、P关于y轴对称,
∴选项A、C错误,
∵M−4,a−2,N−2,a在同一个函数图象上,
∴当x<0时,y随x的增大而增大,
∴选项D错误,选项B正确.
故选:B.
【点睛】此题考查了函数的图象.注意掌握排除法在选择题中的应用是解此题的关键.
2.(2022·青海·统考中考真题)2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A.B.C.D.
【答案】B
【分析】首先看清横轴和纵轴表示的量,然后根据实际情况:汽车行驶的路程y与行驶的时间t之间的关系进行判断即可.
【详解】解:由题意可得函数图像分为三段:第一段由左向右呈下降趋势,第二段与x轴平行,第三段由左向右呈下降趋势,且比第一段更陡,故选项B符合,
随着时间的增多,汽车离剧场的距离越来越近,即离x轴越来越近,排除A、C、D;
故选:B.
【点睛】此题主要考查了函数图象,解题的关键是根据函数图象的性质分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
3.(2023·山东滨州·统考中考真题)由化学知识可知,用pH表示溶液酸碱性的强弱程度,当pH>7时溶液呈碱性,当pH<7时溶液呈酸性.若将给定的NaOH溶液加水稀释,那么在下列图象中,能大致反映NaOH溶液的pH与所加水的体积V之间对应关系的是( )
A. B. C. D.
【答案】B
【分析】根据题意,NaOH溶液呈碱性,随着加入水的体积的增加,溶液的浓度越来越低,pH的值则接近7,据此即可求解.
【详解】解:∵NaOH溶液呈碱性,则pH>7,随着加入水的体积的增加,溶液的浓度越来越低,pH的值则接近7,
故选:B.
【点睛】本题考查了函数的图象,数形结合是解题的关键.
4.(2023·四川·统考中考真题)向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量v的函数关系的大致图象是( )
A. B. C. D.
【答案】D
【分析】从水瓶的构造形状上看,从底部到顶部的变化关系为:开始宽,逐渐细小,再变宽,再从函数的图象上看,选出答案.
【详解】解:从水瓶的构造形状上看,从底部到顶部的变化关系为:开始宽,逐渐细小,再变宽.
则注入的水量v随水深h的变化关系为:先慢再快,最后又变慢,
那么从函数的图象上看,
C对应的图象变化为先快再慢,最后又变快,不符合;
A、B对应的图象中间没有变化,只有D符合条件.
故选:D.
【点睛】本题主要考查函数的定义及函数的图象的关系,抓住变量之间的变化关系是解题的关键.
题型08 画函数图象
【解题技巧】此类题型考查利用列表法画函数图象,根据函数图象获取信息,画出函数图象,从函数图象获取信息是解题的关键.
1.(2022·山东临沂·统考中考真题)杠杆原理在生活中被广泛应用(杠杆原理:阻力×阻力臂=动力×动力臂),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图1).制作方法如下:
第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点O,并用细麻绳固定,在支点O左侧2cm的A处固定一个金属吊钩,作为秤钩;
第二步:取一个质量为0.5kg的金属物体作为秤砣.
(1)图1中,把重物挂在秤钩上,秤砣挂在支点О右侧的B处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,OB的长度随之变化.设重物的质量为xkg,OB的长为ycm.写出y关于x的函数解析式;若0
【答案】(1)y=4x;0
【分析】(1)根据阻力×阻力臂=动力×动力臂解答即可;
(2)根据阻力×阻力臂=动力×动力臂求出解析式,然后根据列表、描点、连线的步骤解答.
【详解】(1)解:∵阻力×阻力臂=动力×动力臂,
∴重物×OA=秤砣×OB.
∵OA=2cm,重物的质量为xkg,OB的长为ycm,秤砣为0.5kg,
∴2x=0.5y,
∴y=4x;
∵4>0,
∴y随x的增大而增大,
∵当y=0时,x=0;当y=48时,x=12,
∴0
∴秤砣×OA=重物×OB.
∵OA=2cm,重物的质量为xkg,OB的长为ycm,秤砣为0.5kg,
∴2×0.5=xy,
∴y=1x;
当x=0.25时,y=10.25=4;
当x=0.5时,y=10.5=2;
当x=1时,y=11=1;
当x=2时,y=12;
当x=4时,y=14;
填表如下:
画图如下:
【点睛】本题考查了一次函数的应用,反比例函数的应用,以及列表、描点、连线画函数图象的方法,求出函数解析式是解答本题的关键.
2.(2023·四川达州·统考中考真题)【背景】在一次物理实验中,小冉同学用一固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R、RL之间关系为I=UR+RL,通过实验得出如下数据:
(1)a=_______,b=_______;
(2)【探究】根据以上实验,构建出函数y=12x+2x≥0,结合表格信息,探究函数y=12x+2x≥0的图象与性质.
①在平面直角坐标系中画出对应函数y=12x+2x≥0的图象;
②随着自变量x的不断增大,函数值y的变化趋势是_________.
(3)【拓展】结合(2)中函数图象分析,当x≥0时,12x+2≥−32x+6的解集为________.
【答案】(1)2,1.5
(2)①见解析;②函数值y逐渐减小
(3)x≥2或x=0
【分析】(1)根据解析式求解即可;
(2)①根据表格数据,描点连线画出函数图象;②根据图象可得出结论;
(3)求出第一象限的交点坐标,结合图象可得结论.
【详解】(1)解:由题意,I=12R+2,
当I=3时,由3=12a+2得a=2,
当R=6时,b=126+2=1.5,
故答案为:2,1.5;
(2)解:①根据表格数据,描点、连线得到函数y=12x+2x≥0的图象如图:
②由图象可知,随着自变量x的不断增大,函数值y逐渐减小,
故答案为:函数值y逐渐减小;
(3)解:当x=2时,y=−32×2+6=3,当x=0时,y=6,
∴函数y=12x+2x≥0与函数y=−32x+6的图象交点坐标为2,3,0,6,
在同一平面直角坐标系中画出函数y=−32x+6的图象,如图,
由图知,当x≥2或x=0时,12x+2≥−32x+6,
即当x≥0时,12x+2≥−32x+6的解集为x≥2或x=0,
故答案为:x≥2或x=0.
【点睛】本题考查函数的图象与性质、描点法画函数图象、两个函数图象的交点问题,根据表格画出函数的图象,并利用数形结合思想探究函数性质是解答的关键.
3.(2022·甘肃兰州·统考中考真题)如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,M为AB边上一动点,BN⊥CM,垂足为N.设A,M两点间的距离为xcm(0≤x≤5),B,N两点间的距离为ycm(当点M和B点重合时,B,N两点间的距离为0).
小明根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,得到了y与x的几组对应值:
请你通过计算,补全表格:a=______;
(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点x,y,并画出函数y关于x的图像;
(3)探究性质:随着自变量x的不断增大,函数y的变化趋势:______.
(4)解决问题:当BN=2AM时,AM的长度大约是______cm.(结果保留两位小数)
【答案】(1)3.2
(2)答案见解析
(3)y随x的增大而减小
(4)1.67
【分析】(1)先求出AB边上的高,进而求出AM',判断出点M与M'重合,即可得出答案;
(2)先描点,再连线,即可画出图像;
(3)根据图像直接得出结论;
(4)利用表格和图像估算出AM的长度.
【详解】(1)解:如图,
在Rt△ABC中,AC=3,BC=4,根据勾股定理得,AC=5,
过点C作CM'⊥AB于M,
∴S△ABC=12AC•BC=12AB•CM',
∴CM'=125,
在Rt△ACM'中,根据勾股定理得,AM'=AC2−CM'2=1.8,
当a=1.8时,点M与点M'重合,
∴CM⊥AB,
∵BN⊥CM,
∴点M,N重合,
∴a=BN=BM=AB﹣AM=3.2,
故答案为:3.2;
(2)解:如图所示,
(3)解:由图像知,y随x的增大而减小,
故答案为:y随x的增大而减小;
(4)解:如图,直线OD的解析式为y=2x,
借助表格和图像得,当BN=2AM时,AM的长度大约是1.67cm,
故答案为:1.67.
【点睛】本题主要考查了勾股定理,三角形的面积,函数图像的画法,画出函数图像是解本题的关键.
4.(2022·湖北襄阳·统考中考真题)探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数y=6|x|−|x|的图象,并探究该函数性质.
(1)绘制函数图象
①列表:下列是x与y的几组对应值,其中a= .
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
(2)探究函数性质,请写出函数y=6|x|-|x|的一条性质: ;
(3)运用函数图象及性质
①写出方程6|x|-|x|=5的解 ;
②写出不等式6|x|-|x|≤1的解集 .
【答案】(1)①1;②见解析,③见解析
(2)y=6|x|−|x|的图象关于y轴对称轴(答案不唯一)
(3)①x=1或x=−1;②x≤−2或x≥2
【分析】(1)①把x=2代入解析式即可得a的值;②③按要求描点,连线即可;
(2)观察函数图象,可得函数性质;
(3)①由函数图象可得答案;②观察函数图象即得答案.
【详解】(1)①列表:当x=2时,a=6|2|−|2|=1,
故答案为:1;
②描点,③连线如下:
(2)观察函数图象可得:y=6|x|−|x|的图象关于y轴对称,
故答案为:y=6|x|−|x|的图象关于y轴对称;
(3)①观察函数图象可得:当y=5时,x=1或x=-1,
6|x|−|x|=5的解是x=1或x=-1,
故答案为:x=1或x=-1,
②观察函数图象可得,当x≤-2或x≥2时,y≤1,
∴6|x|−|x|≤1的解集是x≤-2或x≥2,
故答案为:x≤-2或x≥2.
【点睛】本题考查了列表描点画函数图象,根据函数图象获取信息,画出函数图象,从函数图象获取信息是解题的关键.
题型09 动点问题的函数图象
类型一 动点与函数图象判断的解题策略
方法一:趋势判断法. 根据几何图形的构造特点,对动点运动进行分段,并判断每段对应函数图象的增减变化趋势;
方法二:解析式计算法. 根据题意求出每段的函数解析式,结合解析式对应的函数图象进行判断;
方法三:定点求值法. 结合几何图形特点,在点运动的拐点、垂直点、特殊点处求出函数值,对选项进行排除;
方法四:范围排除法. 根据动点的运动过程,求出两个变量的变化范围,对选项进行排除.
类型二 动点与函数图象计算的解题策略
一看图:注意函数图象横纵坐标分别表示的量与取值范围,以及图象的拐点、最值点等;
二看形:观察题目所给几何图形的特点,运用几何性质分析动点整体运动情况;
三结合:几何动点与函数图象相结合,求出图形中相关线段的长度或图形面积的值;
四计算:结合已知,列出等式,计算未知量,常用勾股定理、面积相等和相似等方法进行计算求解.
1.(2023·河北·统考中考真题)如图是一种轨道示意图,其中ADC和ABC均为半圆,点M,A,C,N依次在同一直线上,且AM=CN.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M→A→D→C→N和N→C→B→A→M.若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( )
A. B. C. D.
【答案】D
【分析】设圆的半径为R,根据机器人移动时最开始的距离为AM+CN+2R,之后同时到达点A,C,两个机器人之间的距离y越来越小,当两个机器人分别沿A→D→C和C→B→A移动时,此时两个机器人之间的距离是直径2R,当机器人分别沿C→N和A→M移动时,此时两个机器人之间的距离越来越大.
【详解】解:由题意可得:机器人(看成点)分别从M,N两点同时出发,
设圆的半径为R,
∴两个机器人最初的距离是AM+CN+2R,
∵两个人机器人速度相同,
∴分别同时到达点A,C,
∴两个机器人之间的距离y越来越小,故排除A,C;
当两个机器人分别沿A→D→C和C→B→A移动时,此时两个机器人之间的距离是直径2R,保持不变,
当机器人分别沿C→N和A→M移动时,此时两个机器人之间的距离越来越大,故排除C,
故选:D.
【点睛】本题考查动点函数图像,找到运动时的特殊点用排除法是关键.
2.(2022·甘肃武威·统考中考真题)如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( )
A.3B.23C.33D.43
【答案】B
【分析】根据图1和图2判定三角形ABD为等边三角形,它的面积为33解答即可.
【详解】解:在菱形ABCD中,∠A=60°,
∴△ABD为等边三角形,
设AB=a,由图2可知,△ABD的面积为33,
∴△ABD的面积=34a2=33
解得:a=23(负值已舍)
故选B
【点睛】本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此题的关键.
3.(2023·广东深圳·统考中考真题)如图1,在Rt△ABC中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中BP长与运动时间t(单位:s)的关系如图2,则AC的长为( )
A.1552B.427C.17D.53
【答案】C
【分析】根据图象可知t=0时,点P与点A重合,得到AB=15,进而求出点P从点A运动到点B所需的时间,进而得到点P从点B运动到点C的时间,求出BC的长,再利用勾股定理求出AC即可.
【详解】解:由图象可知:t=0时,点P与点A重合,
∴AB=15,
∴点P从点A运动到点B所需的时间为15÷2=7.5s;
∴点P从点B运动到点C的时间为11.5−7.5=4s,
∴BC=2×4=8;
在Rt△ABC中:AC=AB2+BC2=17;
故选C.
【点睛】本题考查动点的函数图象,勾股定理.从函数图象中有效的获取信息,求出AB,BC的长,是解题的关键.
4.(2022·山东菏泽·统考中考真题)如图,等腰Rt△ABC与矩形DEFG在同一水平线上,AB=DE=2,DG=3,现将等腰Rt△ABC沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰Rt△ABC与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A.B.C.D.
【答案】B
【分析】根据平移过程,可分三种情况,当0≤x<1时,当1≤x<3时,当3≤x≤4时,利用直角三角形的性质及面积公式分别写出各种情况下y与x的函数关系式,再结合函数图象即可求解.
【详解】过点C作CM⊥AB于N,DG=3,
在等腰Rt△ABC中,AB=2,
∴CN=1,
①当0≤x<1时,如图,CM=x,
∴PQ=2x,
∴y=12⋅PQ⋅CM=12×2x⋅x=x2,
∴0≤x<1,y随x的增大而增大;
②当1≤x<3时,如图,
∴y=S△ABC=12×2×1=1,
∴当1≤x<3时,y是一个定值为1;
③当3≤x≤4时,如图,CM=x−3,
∴PQ=2(x−3),
∴y=12AB⋅CN−12PQ⋅CM=12×2×1−12×2×(x−3)2=1−(x−3)2,
当x=3,y=1,当3
故选:B.
【点睛】本题考查了动点函数问题,涉及二次函数的图象及性质,能够准确理解题意并分情况讨论是解题的关键.
5.(2021·山东聊城·统考中考真题)如图,四边形ABCD中,已知AB∥CD,AB与CD之间的距离为4,AD=5,CD=3,∠ABC=45°,点P,Q同时由A点出发,分别沿边AB,折线ADCB向终点B方向移动,在移动过程中始终保持PQ⊥AB,已知点P的移动速度为每秒1个单位长度,设点P的移动时间为x秒,△APQ的面积为y,则能反映y与x之间函数关系的图象是( )
A.B.C.D.
【答案】B
【分析】依次分析当0≤x≤3、3
∵已知AB∥CD,AB与CD之间的距离为4,
∴DE=CF=4,
∵点P,Q同时由A点出发,分别沿边AB,折线ADCB向终点B方向移动,在移动过程中始终保持PQ⊥AB,
∴PQ∥DE∥CF,
∵AD=5,
∴AE=AD2−DE2=3,
∴当0≤x≤3时,P点在AE之间,此时,AP=t,
∵APAE=PQDE,
∴PQ=43x,
∴S△APQ=12AP⋅PQ=x2×43x=23x2,
因此,当0≤x≤3时,其对应的图像为y=23x20≤x≤3,故排除C和D;
∵CD=3,
∴EF=CD=3,
∴当3
∴BF=CF=4,
∴AB=3+3+4=10,
∴当6
S△AP2Q2=12×10−xx=−12x2+5x,
因此当6
【点睛】本题考查了平行线分线段成比例的推论、勾股定理、平行线的性质、三角形的面积公式、二次函数的图像等内容,解决本题的关键是牢记相关概念与公式,能分情况讨论等,本题蕴含了数形结合与分类讨论的思想方法等.
6.(2022·青海西宁·统考中考真题)如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A. B. C. D.
【答案】A
【分析】过点A向BC作AH⊥BC于点H,所以根据相似三角形的性质可求出EF,进而求出函数关系式,由此即可求出答案.
【详解】解:过点A向BC作AH⊥BC于点H,
根据相似比可知:EFBC=3−x3,
即EF6=3−x3,
解得:EF=2(3-x),
则△DEF的面积y=12×2(3-x)x=-x2+3x=-(x-32)2+94,
故y关于x的函数图象是一个开口向下、顶点坐标为(32,94)的抛物线.
故选:A.
【点睛】本题考查了二次函数图象,主要利用了相似三角形的性质,求出S与x的函数关系式是解题的关键.
一、点的坐标特征及变化
1)点的坐标特征
2)点的坐标变化
3)点到坐标轴的距离
在平面直角坐标系中,已知点P(a,b), 则
1)点P到x轴的距离为b;
2)点P到y轴的距离为a;
3)点P到原点O的距离为P= a2+b2.
4)坐标系内点与点之间的距离
点M(x1,y1)与点N(x2,y2)之间的直线距离(线段长度):MN=(x2−x1)2+(y2−y1)2
若AB∥x轴,则A(xA,y),B(xB,y)的距离为xA−xB;
若AB∥y轴,则A(x,yA),B(x,yB)的距离为yA−yB;
二、函数的知识
函数的取值范围:使函数有意义的自变量的全体取值,叫做自变量的取值范围.
确定函数取值范围的方法: 1)函数解析式为整式时,字母取值范围为全体实数;
2)函数解析式含有分式时,分式的分母不能为零;
3)函数解析式含有二次根式时,被开方数大于等于零;
4)函数解析式中含有指数为零的式子时,底数不能为零;
5)实际问题中函数取值范围要和实际情况相符合,使之有意义.
函数图像上点的坐标与解析式之间的关系:
1)将点的坐标代入到解析式中,如解析式两边成立,则点在解析式上,反之,不在.
2)两个函数图形交点的坐标就是这两个解析式所组成的方程组的解.
函数的三种表示法及其优缺点
解析法:两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做解析法.
列表法:把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系,这种表示法叫做列表法.
图像法:用图像表示函数关系的方法叫做图像法.
1.(2023·江苏盐城·景山中学校考模拟预测)函数y=−1x−x的图象位于( )
A.第四象限B.第三象限C.第二象限D.第一象限
【答案】A
【分析】根据二次根式有意义的条件和函数的解析式可得x>0,y<0,进而求解.
【详解】解:由函数y=−1x−x,可得自变量的范围为:x>0,可得:y<0,
所以函数y=−1x−x的图象位于第四象限,
故选:A.
【点睛】本题考查了函数的图象,正确求得x>0,y<0是解题的关键.
2.(2023·黑龙江绥化·统考模拟预测)如图,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,则点B的对应点B'的坐标是( )
A.−4,1B.−1,2C.4,−1D.1,−2
【答案】D
【分析】在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度;图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.
【详解】解:如图,将线段AB先向右平移5个单位,得到点B2,1,连接OB,将OB绕原点顺时针旋转90°,
则B'对应坐标为1,−2,
故选:D.
【点睛】本题考查了图形的平移与旋转,熟练运用平移与旋转的性质是解题的关键.
3.(2023·河北石家庄·校联考模拟预测)平面直角坐标系中,点A−3,2,B1,4,Cx,y,若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.2,1,2B.6,−3,4C.4,1,0D.1,0,4
【答案】A
【分析】由AC∥x轴,A−3,2,根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
【详解】解:如图,
∵AC∥x轴,
∴C点的纵坐标为与A点的纵坐标相同,即y=2,
∵当BC⊥AC时,线段BC最短,此时BC∥y轴,
∴此时C点的横坐标与B点的横坐标相同,即x=1,
即C1,2,此时BC=4−2=2.
故选:A.
【点睛】本题考查了坐标与图形的性质,熟记点到坐标轴的距离与这个点坐标的区别及点到直线垂线段最短是解题的关键.
4.(2023·湖北黄石·统考模拟预测)如图所示平面直角坐标系,Rt△OAB 中,AO=2,∠A=90°,∠ABO=30°. 将Rt△OAB绕着AB的中点M旋转180°,则点O的对应点的坐标为( )
A.4,3B.4+2,3C.5,3D.5−2,2
【答案】C
【分析】连接O'A并延长交y轴于E,连接BO',求出O'E,OE的长度即可求解.
【详解】解:连接O'A并延长交y轴于E,连接BO',
∵AM=BM,OM=O'M,
∴四边形AOBO'是平行四边形,
∴EO'∥x轴,AO'=OB,
∴AE⊥y轴,
∵AO=2,∠A=90°,∠ABO=30°,
∴∠AOB=60°,OB=2OA=4,
∴∠AOE=30°,
∴AE=12OA=1,OE=32OA=3
∵AO'=OB=4,
∴O'E=1+4=5,
∴点O的对应点O'的坐标为5,3,
故选:C.
【点睛】本题考查了旋转的性质、含30°的直角三角形.掌握相关结论是解题关键.
5.(2023·河北石家庄·校联考二模)一艘海上搜救船在巡逻过程中发现点A处有一艘船发出求救信号,如图是搜救船上显示的雷达示意图,图上标注了以搜救船为中心的等距线(图中所示的同心圆,单位:海里)及角度,要让搜救船在第一时间抵达故障船所在的位置,应该将搜救船的航行方案调整为( )
A.向北偏西150°方向航行4海里B.向南偏西120°方向航行3海里
C.向北偏西60°方向航行4海里D.向东偏北150°方向航行3海里
【答案】C
【分析】根据方向角的定义:以正南或正北为基准,到目标所在线形成的小于90°的角,进行判断即可.
【详解】解:根据方向角的定义可知,搜救船的航行方案调整为向北偏西60°方向航行4海里,
故选:C.
【点睛】本题考查利用方向角确定位置.熟练掌握方向角的定义,是解题的关键.
6.(2023·广东肇庆·统考三模)某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y与x的函数图象.
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变:
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是( )
A.①③B.①④C.②③D.②④
【答案】C
【分析】本题主要考查函数的图象的应用,解题时要能熟练掌握并能学会读图分析是关键.依据题,分析图象变化前后的实际意义即可得答案.
【详解】解:由图可知,点A的纵坐标的相反数表示成本,一次函数的比例系数表示票价.
图(2)对应的方案是:保持票价不变,并降低成本,故①错误,②正确;
图(3)对应的方案是:提高票价,并保持成本不变,故③正确,④错误.
故选:C.
7.(2023·广东东莞·校联考二模)如图,⊙O的半径为2,弦CD垂直直径AB于点E,且E是OA的中点,点P从点E出发(点P与点E不重合),沿E→D→B的路线运动,设AP=x,sin∠APC=y,那么y与x之间的关系图象大致是( )
A.B.C.D.
【答案】C
【分析】本题考查动点问题的函数图象,当点P在线段ED时,y=sin∠APC=AEPA=1x,推出当1
∵弦CD垂直直径AB于点E,且E是OA的中点,OA=2,
∴AE=OE=12OA=1,AD=OD=2,
又AP=x,
∴当点P在线段ED时,y=sin∠APC=AEPA=1x,
∴当1
故选:C.
8.(2023·安徽·模拟预测)如图,△ABC为等腰直角三角形,∠ACB=90°,AB=2,正方形DEFG的边长为1,且AB与DE在同一条直线上,△ABC从点B与点D重合开始,沿直线DE向右平移,直至点A与点E完全重合时停止.设BD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数图像大致是( )
A.B.C.D.
【答案】B
【分析】本题考查了等腰直角三角形的性质,抛物线的解析式及其图像,分割法计算面积,分类思想,图像信息的获取与处理,利用分类思想,表示不同阶段的图形面积,再画出大致图像即可.
【详解】解:①当0≤x≤1时,∵△ABC为等腰直角三角形,∠ACB=90°,AB=2,正方形DEFG的边长为1,
∴∠GDE=90°,∠DBC=45°
∵设BD的长为x,
∴y=12BD2=12x2;
②当1
∴BE=BD−DE=x−1,AD=AB−BD=2−x,
∵∠CAB=∠DBC=45°,
∴y=12AB·GD−12AD2−12BE2
=12×2×1−12(2−x)2−12(x−1)2
=−x2+3x−32=−x−322+34;
③当2
∴y=12AE2
=12(3−x)2.
∴.观察图像,知B项正确,
故选:B.
9.(2023·广东湛江·统考一模)已知点P−m,m−3,当m=−1时,点P在第 象限,当点P在x轴上时,m= .
【答案】 四 3
【分析】本题主要考查了各象限内点的坐标符号特征以及坐标轴上的点的特征,解题的关键是熟记各象限内点的坐标符号.m=−1时,横坐标大于零,纵坐标小于零,即可得出答案,再根据x轴上的点的纵坐标为0,即可求解得m.
【详解】解:m=−1时,−m=1>0,m−3=−4<0,由第四象限+,−,可知点P−m,m−3在第四象限;
当点P在x轴上时,由x轴上的点的纵坐标为0可得m−3=0,解得m=3.
故答案为:四;3.
10.(2023·四川眉山·校考三模)平面直角坐标系内有一点Mx,y,已知x,y满足4x+3+(5y−2)2=0,则点M关于y轴对称的点N在第 象限.
【答案】一
【分析】根据4x+3+(5y−2)2=0得到x=−34,y=25,确定M的位置,后确定对称点的坐标,解答即可.
【详解】∵4x+3+(5y−2)2=0,
∴x=−34,y=25,
∴M−34,25,
∴N34,25,
故点N在第一象限,
故答案为:一.
【点睛】本题考查了实数的非负性,关于y轴对称纵坐标不变,横坐标变相反数,熟练掌握对称点的确定是解题的关键.
11.(2023·陕西西安·西安市曲江第一中学校考模拟预测)中国象棋是一种古老的棋类游戏,大约有两千年的历史,是中华文明非物质文化经典产物.如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点−1,−2,“马”位于点3,−2,则“兵”位于点 .
【答案】−3,1
【分析】由“帅”位于点−1,−2,“马”位于点3,−2,可得每个小方格代表的长度为1,再根据“帅”到“兵”的移动方式即可确定“兵”所在点的坐标.
【详解】解:∵“帅”位于点−1,−2,“马”位于点3,−2,“帅”与“马”相距4个小方格,
∴每个小方格代表的长度为1,“帅”与“马”在直线y=−2上,
由图可知,“帅”向上移动3格,向左移动2格到达“兵”,
∴“兵”位于点−1−2,−2+3上,即−3,1.
故答案为:−3,1.
【点睛】本题考查实际问题中用坐标表示位置,解题的关键是通过已知点坐标得出每个小方格代表的长度.
12.(2023·广西钦州·校考模拟预测)如图所示,在平面直角坐标系中,已知A0,1、B2,0、C4,3.
(1)在平面直角坐标系中画出△ABC,并画出△ABC关于y轴对称的△A1B1C1
(2)已知P为x轴上一点,若△ABP的面积为4.求点P的坐标.
【答案】(1)见解析
(2)P 10,0 或 P 6,0
【分析】(1)确定点B2,0、C4,3关于y轴的对称点B1−2,0、C1−4,3,顺次连接A,B1,C1三点,△A1B1C1即为所求:
(2)由P 为 x 轴上一点,S△ABP=12OA⋅BP=12×1×BP=4,得BP=8,进面求得点坐标.
【详解】(1)解:如图所示,确定点B2,0、C4,3关于y轴的对称点B1−2,0、C1−4,3,顺次连接A,B1,C1三点,△A1B1C1即为所求:
(2)∵ P 为 x 轴上一点,A(0,1)、B(2,0),
∴OA=1,S△ABP=12OA⋅BP=12×1×BP=4.
∴BP=8.
∵B(2,0),
∴ P 点的横坐标为: 2+8=10 或2−8=−6;.
∴P(10,0)或 P(−6,0).
【点睛】本题考查轴对称,直角坐标系内三角形面积计算;直角坐标系内,由点坐标求线段长度是解题的关键.
13.(2023·广东茂名·统考三模)已知函数y=y1+y2,其中y1=(4−a)xa2−4a−1是反比例函数,y2与x−5成正比例,函数的自变量x的取值范围是x≥12,且当x=2时,y=−1.
(1)解析式探究,根据给定的条件,可以确定出该函数的解析式为:
(2)下表是y与x的几组对应值
表中表中m= ,n=
(3)根据表中数据,在平面直角坐标系中,描点并画出该函数的图象;
(4)结合画出的函数图象,解决问题:
估计y1+y2=−x+5时,x的值约为 (精确到0.1).
【答案】(1)y=4x+x−5(x≥12),
(2)72;53
(3)详见解析
(4)4.6
【分析】本题考查了反比例函数的图象,函数和方程的关系,数形结合是解题的关键.
(1)求得y1用待定系数法设y2=k2x−5),则y=4x+k(x−5),将已知条件代入得关于k方程组,即可求得该函数解析式;
(2)把x=12和x=6分别代入(1)求得的解析式,即可求得m、n的值;
(3)在平面直角坐标系中描点,用平滑曲线从左到右顺次连接各点,画出图象;
(3)函数y=y1+y2和直线y=−x+5的交点在4和5之间,通过分析得出结论.
【详解】(1)∵y1=(4−a)xa2−4a−1是反比例函数,
∴4−a≠0且a2−4a−1=−1,
解得a=0,
∴y1=4x,
设y2=k(x−5),则y=4x+k(x−5),
∵当x=2时,y=−1.
∴−1=42+k(2−5),
解得k=1,
∴y=4x+x−5(x≥12),
故答案为:y=4x+x−5(x≥12),
(2)把x=12代入y=4x+x−5得,y=72,
∴m=72,
把x=6代入y=4x+x−5得,y=53,
∴n=53,
故答案为72,53;
(3)根据表中数据,在平面直角坐标系中描点,画出图象.
(4)观察图象,函数y=y1+y2和直线y=−x+5的交点在4和5之间,
当x=4.5时,y=4x+x−5≈0.4,y=−x+5=0.5,
当x=4.6时,y=4x+x−5≈0.47,y=−x+5=0.4,
当x=4.7时,y=4x+x−5≈0.55,y=−x+5=0.3,
∴估计y1+y2=−x+5时,x的值约为4.6,
故答案为4.6.
考点二 一次函数、反比例函数、二次函数的性质
题型01 正比例函数的图象与性质
1.(2021·湖南益阳·统考中考真题)正比例函数y=2x与反比例函数y=2x的图象或性质的共有特征之一是( )
A.函数值y随x的增大而增大B.图象在第一、三象限都有分布
C.图象与坐标轴有交点D.图象经过点2,1
【答案】B
【分析】根据正比例函数和反比例函数的图象与性质逐项判断即可得.
【详解】A、正比例函数y=2x,函数值y随x的增大而增大;反比例函数y=2x,在每一象限内,函数值y随x的增大而减小,则此项不符题意;
B、正比例函数y=2x的图象在第一、三象限都有分布,反比例函数y=2x的图象在第一、三象限都有分布,则此项符合题意;
C、正比例函数y=2x的图象与坐标轴的交点为原点,反比例函数y=2x的图象与坐标轴没有交点,则此项不符题意;
D、正比例函数y=2x,当x=2时,y=4,即其图象经过点2,4,不经过点2,1,则此项不符题意;
故选:B.
【点睛】本题考查了正比例函数和反比例函数的图象与性质,熟练掌握正比例函数和反比例函数的图象与性质是解题关键.
2.(2023·甘肃武威·统考中考真题)若直线y=kx(k是常数,k≠0)经过第一、第三象限,则k的值可为( )
A.−2B.−1C.−12D.2
【答案】D
【分析】通过经过的象限判断比例系数k的取值范围,进而得出答案.
【详解】∵直线y=kx(k是常数,k≠0)经过第一、第三象限,
∴k>0,
∴k的值可为2,
故选:D.
【点睛】本题考查正比例函数的图象与性质,熟记比例系数与图象经过的象限之间的关系是解题的关键.
3.(2021·四川成都模拟预测)在正比例函数y=kx中,y的值随着x值的增大而减小,则点P3,k在第 象限.
【答案】四
【详解】解:∵正比例函数y=kx中,函数y的值随x值的增大而减小,
∴k<0,
∴点P3,k在第四象限.
故答案为:四.
4.(2023·山东·统考中考真题)一个函数过点1,3,且y随x增大而增大,请写出一个符合上述条件的函数解析式 .
【答案】y=3x(答案不唯一)
【分析】根据题意及函数的性质可进行求解.
【详解】解:由一个函数过点1,3,且y随x增大而增大,可知该函数可以为y=3x(答案不唯一);
故答案为y=3x(答案不唯一).
【点睛】本题主要考查正比例函数的性质,熟练掌握正比例函数的性质是解题的关键.
题型02 求一次函数解析式
确定一次函数解析式的方法:1)依据题意中等量关系直接列出解析式;2)待定系数法.
用待定系数法求一次函数表达式的一般步骤:
1)设出函数的一般形式y=kx(k≠0)或y=kx+b(k≠0);
2)根据已知条件(自变量与函数的对应值)代入表达式得到关于待定系数的方程或方程组;
3)解方程或方程组求出k,b的值;
4)将所求得的k,b的值代入到函数的一般形式中,从而得到一次函数解析式.
1.(2023·江苏苏州·统考中考真题)已知一次函数y=kx+b的图象经过点1,3和−1,2,则k2−b2= .
【答案】−6
【分析】把点1,3和−1,2代入y=kx+b,可得k+b=3k−b=−2,再整体代入求值即可.
【详解】解:∵一次函数y=kx+b的图象经过点1,3和−1,2,
∴k+b=3−k+b=2,即k+b=3k−b=−2,
∴k2−b2=k+bk−b=3×−2=−6;
故答案为:−6
【点睛】本题考查的是一次函数的性质,利用待定系数法求解一次函数的解析式,利用平方差公式分解因式,熟练的利用平方差公式求解代数式的值是解本题的关键.
2.(2022·湖南益阳·统考中考真题)如图,直线y=12x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的点B(0,2)的直线设为y=kx+b.
(1)求点A′的坐标;
(2)确定直线A′B对应的函数表达式.
【答案】(1)A′(2,0)
(2)y=﹣x+2
【分析】(1)利用直线解析式求得点A坐标,利用关于y轴的对称点的坐标的特征解答即可;
(2)利用待定系数法解答即可.
【详解】(1)解:令y=0,则12x+1=0,
∴x=﹣2,
∴A(﹣2,0).
∵点A关于y轴的对称点为A′,
∴A′(2,0).
(2)解:设直线A′B的函数表达式为y=kx+b,
∴2k+b=0b=2,
解得:k=−1b=2,
∴直线A′B对应的函数表达式为y=﹣x+2.
【点睛】本题主要考查了一次函数图象的性质、一次函数图象上点的坐标的特征、待定系数法确定函数的解析式、关于y轴的对称点的坐标的特征等知识,利用待定系数法求函数解析式是解题的关键.
3.(2023·浙江温州·统考中考真题)如图,在直角坐标系中,点A2,m在直线y=2x−52上,过点A的直线交y轴于点B0,3.
(1)求m的值和直线AB的函数表达式.
(2)若点Pt,y1在线段AB上,点Qt−1,y2在直线y=2x−52上,求y1−y2的最大值.
【答案】(1)m=32,y=−34x+3
(2)152
【分析】(1)把点A的坐标代入直线解析式可求解m,然后设直线AB的函数解析式为y=kx+b,进而根据待定系数法可进行求解函数解析式;
(2)由(1)及题意易得y1=−34t+30≤t≤2,y2=2t−1−52=2t−92,则有y1−y2=−34t+3−2t−92=−114t+152,然后根据一次函数的性质可进行求解.
【详解】(1)解:把点A2,m代入y=2x−52,得m=32.
设直线AB的函数表达式为y=kx+b,把点A2,32,B0,3代入得
2k+b=32b=3.,解得k=−34b=3.,
∴直线AB的函数表达式为y=−34x+3.
(2)解:∵点Pt,y1在线段AB上,点Qt−1,y2在直线y=2x−52上,
∴y1=−34t+30≤t≤2,y2=2t−1−52=2t−92,
∴y1−y2=−34t+3−2t−92=−114t+152.
∵k=−114<0,
∴y1−y2的值随x的增大而减小,
∴当t=0时,y1−y2的最大值为152.
【点睛】本题主要考查一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题的关键.
题型03一次函数的图象与性质
一、在直线y=kx+b(k≠0)中,令y=0,则x=−bk ,即直线y=kx+b与x轴交于(−bk,0)
令x=0,则y=b,即直线y=kx+b与y轴交于(0,b)
1)当−bk > 0时,即k,b异号时,直线与x轴交于正半轴.
2)当−bk = 0,即b=0时,直线经过原点.
3)当−b k < 0,即k,b同号时,直线与x轴交于负半轴.
二、两个一次函数表达式(直线l1:y1=k1x+b1与l2:y2=k2x+b2)的位置关系:
1)当k1=k2,b1=b2时,两直线重合;
2) 当k1=k2,b1≠b2时,两直线平行;
3)当k1≠k2,b1=b2时,两直线交于y轴上的同一点(0,b);
4)当k1•k2=-1时,两直线垂直;
5)当k1≠k2时,两直线相交.
1.(2023·山东临沂·统考中考真题)对于某个一次函数y=kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A.k>0B.kb<0C.k+b>0D.k=−12b
【答案】C
【分析】首先根据一次函数的性质确定k,b的符号,再确定一次函数y=kx+b (k≠0)系数的符号,判断出函数图象所经过的象限.
【详解】解:∵一次函数y=kx+b的图象不经过第二象限,
∴k>0,b<0,故选项A正确,不符合题意;
∴kb<0,故选项B正确,不符合题意;
∵一次函数y=kx+b的图象经过点2,0,
∴2k+b=0,则b=−2k,
∴k+b=k−2k=−k<0,故选项C错误,符合题意;
∵b=−2k,
∴k=−12b,故选项D正确,不符合题意;
故选:C.
【点睛】本题考查一次函数图象与系数的关系,解决此类题目的关键是确定k、b的正负.
2.(2022·安徽·统考中考真题)在同一平面直角坐标系中,一次函数y=ax+a2与y=a2x+a的图像可能是( )
A.B.C.D.
【答案】D
【分析】分为a>0和a<0两种情况,利用一次函数图像的性质进行判断即可.
【详解】解:当x=1时,两个函数的函数值:y=a+a2,即两个图像都过点1,a+a2,故选项A、C不符合题意;
当a>0时,a2>0,一次函数y=ax+a2经过一、二、三象限,一次函数y=a2x+a经过一、二、三象限,都与y轴正半轴有交点,故选项B不符合题意;
当a<0时,a2>0,一次函数y=ax+a2经过一、二、四象限,与y轴正半轴有交点,一次函数y=a2x+a经过一、三、四象限,与y轴负半轴有交点,故选项D符合题意.
故选:D.
【点睛】本题主要考查了一次函数的图像性质.理解和掌握它的性质是解题的关键.
一次函数y=kx+b的图像有四种情况:
①当k>0,b>0时,函数y=kx+b的图像经过第一、二、三象限;
②当k>0,b<0时,函数y=kx+b的图像经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图像经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图像经过第二、三、四象限.
3.(2023·江苏无锡·统考中考真题)将函数y=2x+1的图像向下平移2个单位长度,所得图像对应的函数表达式是( )
A.y=2x−1B.y=2x+3C.y=4x−3D.y=4x+5
【答案】A
【分析】根据题目条件函数y=2x+1的图像向下平移2个单位长度,则b的值减少2,代入方程中即可.
【详解】解:∵函数y=2x+1的图像向下平移2个单位长度,
∴y=2x+1−2=2x−1,
故答案为:A.
【点睛】本题主要考查函数平移,根据题目信息判断是沿y轴移动还是沿x轴移动是解题的关键.
4.(2021·江苏苏州·统考中考真题)已知点A2,m,B32,n在一次函数y=2x+1的图像上,则m与n的大小关系是( )
A.m>nB.m=nC.m
【分析】根据一次函数的增减性加以判断即可.
【详解】解:在一次函数y=2x+1中,
∵k=2>0,
∴y随x的增大而增大.
∵2<94,
∴2<32.
∴m
【点睛】本题考查了一次函数的性质、实数的大小比较等知识点,熟知一次函数的性质是解题的关键.
5.(2022·内蒙古包头·中考真题)在一次函数y=−5ax+b(a≠0)中,y的值随x值的增大而增大,且ab>0,则点A(a,b)在( )
A.第四象限B.第三象限C.第二象限D.第一象限
【答案】B
【分析】根据一次函数的性质求出a的范围,再根据每个象限点的坐标特征判断A点所处的象限即可.
【详解】∵在一次函数y=−5ax+b(a≠0)中,y的值随x值的增大而增大,
∴−5a>0,即a<0,
又∵ab>0,
∴b<0,
∴点A(a,b)在第三象限,
故选:B
【点睛】本题考查了一次函数的性质和各个象限坐标特点,能熟记一次函数的性质是解此题的关键.
6.(2021·江苏扬州·统考中考真题)如图,一次函数y=x+2的图像与x轴、y轴分别交于点A、B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为( )
A.6+2B.32C.2+3D.3+2
【答案】A
【分析】根据一次函数表达式求出点A和点B坐标,得到△OAB为等腰直角三角形和AB的长,过点C作CD⊥AB,垂足为D,证明△ACD为等腰直角三角形,设CD=AD=x,结合旋转的度数,用两种方法表示出BD,得到关于x的方程,解之即可.
【详解】解:∵一次函数y=x+2的图像与x轴、y轴分别交于点A、B,
令x=0,则y=2,令y=0,则x=−2,
则A(−2,0),B(0,2),
则△OAB为等腰直角三角形,∠ABO=45°,
∴AB=22+22=2,
过点C作CD⊥AB,垂足为D,
∵∠CAD=∠OAB=45°,
∴△ACD为等腰直角三角形,设CD=AD=x,
∴AC=AD2+CD2=2x,
∵旋转,
∴∠ABC=30°,
∴BC=2CD=2x,
∴BD=BC2−CD2=3x,
又BD=AB+AD=2+x,
∴2+x=3x,
解得:x=3+1,
∴AC=2x=2(3+1)=6+2,
故选A.
【点睛】本题考查了一次函数与坐标轴的交点问题,等腰直角三角形的判定和性质,直角三角形的性质,勾股定理,二次根式的混合运算,知识点较多,解题的关键是作出辅助线,构造特殊三角形.
7.(2023·四川南充·统考中考真题)如图,直线y=kx−2k+3(k为常数,k<0)与x,y轴分别交于点A,B,则2OA+3OB的值是 .
【答案】1
【分析】根据一次函数解析式得出OA=2k−3k,OB=−2k+3,然后代入化简即可.
【详解】解:y=kx−2k+3,
∴当y=0时,x=−3k+2,当x=0时,y=−2k+3,
∴OA=−3k+2=2k−3k,OB=−2k+3,
∴2OA+3OB=22k−3k+33−2k=2k2k−3−32k−3=2k−32k−3=1,
故答案为:1.
【点睛】题目主要考查一次函数与坐标轴的交点及求代数式的值,熟练掌握一次函数的性质是解题关键.
8.(2022·浙江绍兴·统考中考真题)已知(x1,y1),(x2,y2),(x3,y3)为直线y=−2x+3上的三个点,且x1
C.若x2x3>0,则y1y3>0D.若x2x3<0,则y1y2>0
【答案】D
【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.
【详解】解:∵直线y=−2x+3
∴y随x增大而减小,当y=0时,x=1.5
∵(x1,y1),(x2,y2),(x3,y3)为直线y=−2x+3上的三个点,且x1
若x1x3<0,则x1,x3异号,但不能确定y1y2的正负,故选项B不符合题意;
若x2x3>0,则x2,x3同号,但不能确定y1y3的正负,故选项C不符合题意;
若x2x3<0,则x2,x3异号,则x1,x2同时为负,故y1,y2同时为正,故y1y2>0,故选项D符合题意.
故选:D.
【点睛】本题考查一次函数图象上点的坐标特征,解题的关键是明确题意,利用一次函数的性质解答.
题型04 一次函数与方程、不等式
一、一次函数与一元一次方程
思路:由于任何一个一元一次方程可以转化为ax+b=0(a、b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求自变量的值.
从“数”上看:方程ax+b = 0(a≠0)的解⇔函数y=ax+b(a≠0)中,y=0时对应的x的值
从“形”上看:方程ax+b = 0 (a≠0)的解⇔函数y=ax+b(a≠0)的图像与x轴交点的横坐标.
二、一次函数与二元一次方程组
思路:一般地,二元一次方程mx+ny=p(m、n、p是常数,且m≠0,n≠0)都能写成y=ax+b(a、b为常数,且a≠0)的形式.因此,一个二元一次方程对应一个一次函数,又因为一个一次函数对应一条直线,所以一个二元一次方程也对应一条直线,进一步可知,一个二元一次方程组对应两个一次函数,因而也对应两条直线.
从“数”的角度看:解二元一次方程组相当于考虑自变量为何值时,两个函数的值相等,以及这两个函数值是何值;
从“形”的角度看:解二元一次方程组相当于确定两条直线的交点坐标,一般地,如果一个二元一次方程组有唯一解,那么这个解就是方程组对应的两条直线的交点坐标.
三、一次函数与一元一次不等式
思路:关于x的一元一次不等式kx+b>0(或<0)的解集是以直线y=kx+b和x轴的交点为分界点,x轴上(下)方的图象所对应的x的取值范围.
从函数的角度看:解一元一次不等式就是寻求使一次函数y=ax+b(a≠0)的值大于(或小于)0的自变量的取值范围;
从函数图象的角度看:就是确定直线y=ax+b(a≠0)在x轴上(或下)方部分的横坐标满足的条件.
1.(2022·广西梧州·统考中考真题)如图,在平面直角坐标系中,直线y=2x+b与直线y=−3x+6相交于点A,则关于x,y的二元一次方程组y=2x+by=−3x+6的解是( )
A.x=2y=0B.x=1y=3C.x=−1y=9D.x=3y=1
【答案】B
【分析】由图象交点坐标可得方程组的解.
【详解】解:由图象可得直线y=2x+b与直线y=−3x+6相交于点A(1,3),
∴关于x,y的二元一次方程组y=2x+by=−3x+6的解是x=1y=3.
故选:B.
【点睛】本题考查一次函数与二元一次方程的关系,解题关键是理解直线交点坐标中x与y的值为方程组的解.
2.(2023·宁夏·统考中考真题)在同一平面直角坐标系中,一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图象如图所示,则下列结论错误的是( )
A.y1随x的增大而增大
B.b
D.关于x,y的方程组ax−y=−bmx−y=−n的解为x=2y=3
【答案】C
【分析】结合图象,逐一进行判断即可.
【详解】解:A、y1随x的增大而增大,故选项A正确;
B、由图象可知,一次函数y1=ax+b(a≠0)的图象与y轴的交点在y2=mx+n(m≠0)的图象与y轴的交点的下方,即b
∴关于x,y的方程组ax−y=−bmx−y=−n的解为x=2y=3;
故选项D正确;
故选C.
【点睛】本题考查一次函数的图象和性质,一次函数与二元一次方程组,一次函数与一元一次不等式.从函数图象中有效的获取信息,熟练掌握图象法解方程组和不等式,是解题的关键.
3.(2022·贵州贵阳·统考中考真题)在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a
②方程组{y−ax=by−mx=n的解为{x=−3y=2;
③方程mx+n=0的解为x=2;
④当x=0时,ax+b=−1.
其中结论正确的个数是( )
A.1B.2C.3D.4
【答案】B
【分析】由函数图象经过的象限可判断①,由两个一次函数的交点坐标可判断②,由一次函数与坐标轴的交点坐标可判断③④,从而可得答案.
【详解】解:由一次函数y=mx+n的图象过一,二,四象限,y的值随着x值的增大而减小;
故①不符合题意;
由图象可得方程组y=ax+by=mx+n的解为x=−3y=2,即方程组y−ax=by−mx=n的解为x=−3y=2;
故②符合题意;
由一次函数y=mx+n的图象过2,0, 则方程mx+n=0的解为x=2;故③符合题意;
由一次函数y=ax+b的图象过0,−2, 则当x=0时,ax+b=−2.故④不符合题意;
综上:符合题意的有②③,
故选B
【点睛】本题考查的是一次函数的性质,一次函数的图象的交点坐标与二元一次方程组的解,一次函数与坐标轴的交点问题,熟练的运用数形结合的方法解题是关键.
题型05 求反比例函数解析式
待定系数法求反比例函数解析式的一般步骤:
1)设反比例函数的解析式为y=kx(k为常数,k≠0);
2)把已知的一对x,y的值带入解析式,得到一个关于待定系数k的方程;
3)解方程求出待定系数k;
4)将所求的k值代入所设解析式中.
【说明】由于在反比例函数中,只有一个待定系数,因此只需要一对对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.
1.(2023·北京·统考中考真题)在平面直角坐标系xOy中,若函数y=kxk≠0的图象经过点A−3,2和Bm,−2,则m的值为 .
【答案】3
【分析】先把点A坐标代入求出反比例函数解析式,再把点B代入即可求出m的值.
【详解】解:∵函数y=kxk≠0的图象经过点A−3,2和Bm,−2
∴把点A−3,2代入得k=−3×2=−6,
∴反比例函数解析式为y=−6x,
把点Bm,−2代入得:−2=−6m,
解得:m=3,
故答案为:3.
【点睛】本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征,熟知反比例函数图象上的点的坐标一定满足函数解析式是解题的关键.
2.(2023·河北·统考中考真题)如图,已知点A(3,3),B(3,1),反比例函数y=kx(k≠0)图像的一支与线段AB有交点,写出一个符合条件的k的数值: .
【答案】4(答案不唯一,满足3≤k≤9均可)
【分析】先分别求得反比例函数y=kx(k≠0)图像过A、B时k的值,从而确定k的取值范围,然后确定符合条件k的值即可.
【详解】解:当反比例函数y=kx(k≠0)图像过A(3,3)时,k=3×3=9;
当反比例函数y=kx(k≠0)图像过B(3,1)时,k=3×1=3;
∴k的取值范围为3≤k≤9
∴k可以取4.
故答案为4(答案不唯一,满足3≤k≤9均可).
【点睛】本题主要考查了求反比例函数的解析式,确定边界点的k的值是解答本题的关键.
3.(2023·湖南常德·统考中考真题)如图所示,一次函数y1=−x+m与反比例函数y2=kx相交于点A和点B3,−1.
(1)求m的值和反比例函数解析式;
(2)当y1>y2时,求x的取值范围.
【答案】(1)m=2,y=−3x
(2)x<−1或0
(2)观察函数图象,写出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.
【详解】(1)将点B3,−1代入y1=−x+m得:−3+m=−1
解得:m=2
将B3,−1代入y2=kx得:k=3×−1=−3
∴y2=−3x
(2)由y1=y2得:−x+2=−3x,解得x1=−1,x2=3
所以A,B的坐标分别为A−1,3,B3,−1
由图形可得:当x<−1或0
【点睛】本题考查了反比例函数与一次函数的交点问题,解决本题的关键是掌握反比例函数与一次函数的性质.
题型06 反比例函数的性质
1)反比例函数的图象不是连续的,因此在描述反比例函数的增减性时,一定要有“在其每个象限内”这个前提.当k>0时,在每一象限(第一、三象限)内y随x的增大而减小,但不能笼统地说当k>0时,y随x的增大而减小.同样,当k<0时,也不能笼统地说y随x的增大而增大.
2)反比例函数图象的位置和函数的增减性,都是由常数k的符号决定的,反过来,由双曲线所在位置和函数的增减性,也可以推断出k的符号.
3)双曲线是由两个分支组成的,一般不说两个分支经过第一、三象限(或第二、四象限),而说图象的两个分支分别在第一、三象限(或第二、四象限).
1.(2021·贵州遵义·统考中考真题)已知反比例函数y=kx(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限B.第一、三、四象限
C.第一、二、四象限D.第二、三、四象限
【答案】C
【分析】由反比例函数的图象的分别确定k<0, 再确定一次函数y=kx+2的图象经过的象限即可得到答案.
【详解】解:∵ 反比例函数y=kx(k≠0)的图象分布在二,四象限,
∴k<0,
∴ 一次函数y=kx+2的图象经过一,二,四象限,
故选:C.
【点睛】本题考查的是一次函数与反比例函数的图象与性质,掌握一次函数与反比例函数的图象与k,b的关系是解题的关键.
2.(2021·贵州黔西·中考真题)对于反比例函数y=﹣5x,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
【答案】C
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.
【详解】解:反比例函数y=﹣5x,
A、当x=1时,y=﹣51=﹣5,图像经过点(1,-5),故选项A不符合题意;
B、∵k=﹣5<0,故该函数图象位于第二、四象限,故选项B不符合题意;
C、当x<0时,y随x的增大而增大,故选项C符合题意;
D、当x>0时,y随x的增大而增大,故选项D不符合题意;
故选C.
【点睛】本题考查的是反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
3.(2022·广东·统考中考真题)点1,y1,2,y2,3,y3,4,y4在反比例函数y=4x图象上,则y1,y2,y3,y4中最小的是( )
A.y1B.y2C.y3D.y4
【答案】D
【分析】根据反比例函数的性质,当k>0时,在每一个向西安内,y随x的增大而减少,可直接进行求解.
【详解】解:由反比例函数解析式y=4x可知:4>0,
∴在每个象限内,y随x的增大而减小,
∵点1,y1,2,y2,3,y3,4,y4在反比例函数y=4x图象上,
∴y1>y2>y3>y4,
故选D.
【点睛】本题主要考查反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
4.(2022·四川成都·统考中考真题)若反比例函数y=m−2x的图像经过第二、四象限,则m的取值范围是 .
【答案】m<2
【分析】由反比例函数图像经过第二、四象限,得出m﹣2<0,求出m范围即可.
【详解】解:∵反比例函数y=m−2x的图像经过第二、四象限,
∴m﹣2<0,
得:m<2.
故答案为:m<2.
【点睛】本题主要考查了反比例函数图像的性质,根据反比例函数图像的性质,列出关于m的不等式,是解题的关键.
5.(2020·广东广州·统考中考真题)已知反比例函数y=kx的图象分别位于第二、第四象限,化简:k2k−4−16k−4+(k+1)2−4k.
【答案】5
【分析】由反比例函数图象的性质可得k<0,化简分式时注意去绝对值.
【详解】由题意得k<0.
k2k−4−16k−4+(k+1)2−4k=k2−16k−4+k2+2k+1−4k=k+4k−4k−4+k2−2k+1 =k+4+k−12=k+4+k−1=k+4−k+1=5
【点睛】本题考查反比例函数图象的性质和分式的化简,关键在于去绝对值时符号的问题.
题型07 反比例函数k的几何意义
1.(2023·湖南湘西·统考中考真题)如图,点A在函数y=2x(x>0)的图象上,点B在函数y=3x(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
A.1B.2C.3D.4
【答案】B
【分析】延长BA交y轴于点D,根据反比例函数k值的几何意义得到S△ADO=12×2=1,S矩形OCBD=3,根据四边形ABCO的面积等于S矩形OCBD−S△ADO,即可得解.
【详解】解:延长BA交y轴于点D,
∵AB∥x轴,
∴DA⊥y轴,
∵点A在函数y=2x(x>0)的图象上,
∴S△ADO=12×2=1,
∵BC⊥x轴于点C,DB⊥y轴,点B在函数y=3x(x>0)的图象上,
∴S矩形OCBD=3,
∴四边形ABCO的面积等于S矩形OCBD−S△ADO=3−1=2;
故选B.
【点睛】本题考查反比例函数与几何图形的综合应用.熟练掌握反比例函数中k的几何意义,是解题的关键.
2.(2022·湖南郴州·统考中考真题)如图,在函数y=2xx>0的图像上任取一点A,过点A作y轴的垂线交函数y=−8xx<0的图像于点B,连接OA,OB,则△AOB的面积是( )
A.3B.5C.6D.10
【答案】B
【分析】作AD⊥x轴,BC⊥x轴,由SΔOBE=12SOCBE,SΔAOE=12SADOE即可求解;
【详解】解:如图,作AD⊥x轴,BC⊥x轴,
∵SOCBE=BC⋅BE=8,SADOE=AD⋅AE=2
∴SOCBE+SADOE=10
∵SΔOBE=12SOCBE,SΔAOE=12SADOE
∴SΔAOB=SΔOBE+SΔAOE=12SOCBE+SADOE=5
故选:B.
【点睛】本题主要考查反比例函数的应用,掌握反比例函数相关知识,结合图像进行求解是解题的关键.
3.(2023·福建·统考中考真题)如图,正方形四个顶点分别位于两个反比例函数y=3x和y=nx的图象的四个分支上,则实数n的值为( )
A.−3B.−13C.13D.3
【答案】A
【分析】如图所示,点B在y=3x上,证明△AOC≌△OBD,根据k的几何意义即可求解.
【详解】解:如图所示,连接正方形的对角线,过点A,B分别作x轴的垂线,垂足分别为C,D,点B在y=3x上,
∵OB=OA,∠AOB=∠BDO=∠ACO=90°,
∴∠CAO=90°−∠AOC=∠BOD.
∴△AOC≌△OBD.
∴S△AOC=S△OBD=32 =n2.
∵A点在第二象限,
∴n=−3.
故选:A.
【点睛】本题考查了正方形的性质,反比例函数的k的几何意义,熟练掌握以上知识是解题的关键.
4.(2023·浙江衢州·统考中考真题)如图,点A、B在x轴上,分别以OA,AB为边,在x轴上方作正方形OACD,ABEF.反比例函数y=kxk>0的图象分别交边CD,BE于点P,Q.作PM⊥x轴于点M,QN⊥y轴于点N.若OA=2AB,Q为BE的中点,且阴影部分面积等于6,则k的值为 .
【答案】24
【分析】设OA=4a,则AB=2a,从而可得A4a,0、B6a,0,由正方形的性质可得C4a,4a,由QN⊥y轴,点P在CD上,可得Pk4a,4a,由于Q为BE的中点,BE⊥x轴,可得BQ=12AB=a,则Q6a,a,由于点Q在反比例函数y=kxk>0的图象上可得k=6a2,根据阴影部分为矩形,且长为k4a,宽为a,面积为6,从而可得12×4ak×a=6,即可求解.
【详解】解:设OA=4a,
∵OA=2AB,
∴AB=2a,
∴OB=AB+OA=6a,
∴B6a,0,
在正方形ABEF中,AB=BE=2a,
∵Q为BE的中点,
∴BQ=12AB=a,
∴Q6a,a,
∵Q在反比例函数y=kxk>0的图象上,
∴k=6a×a=6a2,
∵四边形OACD是正方形,
∴C6a,6a,
∵P在CD上,
∴P点纵坐标为4a,
∵P点在反比例函数y=kxk>0的图象上,
∴P点横坐标为x=k4a,
∴Pk4a,4a,
∵∠HMO=∠HNO=∠NOM=90°,
∴四边形OMHN是矩形,
∴NH=k4a,MH=a,
∴S▭OMHN=NH×MH=k4a×a=6,
∴k=24,
故答案为:24.
【点睛】本题考查反比例函数图象的性质及正方形的性质及矩形的面积公式,读懂题意,灵活运用所学知识是解题的关键.
5.(2023·湖北黄石·统考中考真题)如图,点Aa,5a和Bb,5b在反比例函数y=kxk>0的图象上,其中a>b>0.过点A作AC⊥x轴于点C,则△AOC的面积为 ;若△AOB的面积为154,则ab= .
【答案】 52 2
【分析】根据Aa,5a,得出OC=a,AC=5a,根据三角形面积公式,即可求出△AOC的面积;过点B作BD⊥x轴于点D,BD交OA于点E,根据S△OBD=S△ODE+S△OBE=52,S△AOC=S△ODE+S四边形DCAE=52,得出S△OBE=S四边形DCAE,进而得出S△AOB=S梯形BDCA,根据梯形面积公式,列出方程,化简得ab−ba=32,令x=ab,则x−1x=32,求出x的值,根据a>b>0,得出ab>1,即x>1,即可解答.
【详解】解:∵Aa,5a,
∴OC=a,AC=5a,
∴S△AOC=12OC⋅AC=12⋅a⋅5a=52,
过点B作BD⊥x轴于点D,BD交OA于点E,
∵Bb,5b,
∴OD=b,BD=5b,
∴S△OBD=12OD⋅BD=12⋅5b⋅b=52,
∵S△OBD=S△ODE+S△OBE=52,S△AOC=S△ODE+S四边形DCAE=52,
∴S△OBE=S四边形DCAE,
∴S△AOB=S△OBE+S△ABE=S四边形DCAE+S△ABE=S梯形BDCA,
∴S梯形BDCA=12CDAC+BD=12×a−b5a+5b=154,
整理得:ab−ba=32,
令x=ab,
则x−1x=32,
解得:x1=−12(舍),x2=2,
∵a>b>0,
∴ab>1,即x>1,
∴ab=2,
故答案为:52,2.
【点睛】本题主要考查了反比例函数的图象和性质,解题的关键是是掌握反比例函数图象上点的坐标特征,灵活运用面积关系建立方程.
6.(2023·浙江绍兴·统考中考真题)如图,在平面直角坐标系xOy中,函数y=kx(k为大于0的常数,x>0)图象上的两点Ax1,y1,Bx2,y2,满足x2=2x1.△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是 .
【答案】2
【分析】过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BE⊥x于点E,利用S五边形FABEO=S△AFO+S△ABO+S△BOE=k+6,S五边形FABEO=S矩形AFOD+S梯形ADEB=k+S梯形ADEB,得到S梯形ADEB=6,结合梯形的面积公式解得x1y1=8,再由三角形面积公式计算S△ABC=12AC⋅BC=12(x2−x1)⋅(y1−y2)=12x1⋅12y1=14x1y1,即可解答.
【详解】解:如图,过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BE⊥x于点E,
∵S五边形FABEO=S△AFO+S△ABO+S△BOE=k+6
S五边形FABEO=S矩形AFOD+S梯形ADEB=k+S梯形ADEB
∴S梯形ADEB=6
∴(y2+y1)(x2−x1)2=6
∵ x2=2x1
∴y2=12y1
∴(y2+y1)(x2−x1)2=(12y1+y1)(2x1−x1)2=34y1x1=6
∴x1y1=8
∴k=8
S△ABC=12AC⋅BC=12(x2−x1)⋅(y1−y2)=12x1⋅12y1=14x1y1=14×8=2
故答案为:2.
【点睛】本题考查反比例函数中k的几何意义,是重要考点,掌握相关知识是解题关键.
题型08 反比例函数与一次函数综合
1.涉及自变量取值范围
当一次函数与反比例函数相交时,联立两个解析式,构造方程组,然后求出交点坐标.针对y1>y2时自变量x的取值范围,只需观察一次函数的图象高于反比例函数图象的部分所对应的x的范围.例如,如下图,当y1>y2时,x的取值范围为x>xA或xB
1)从图象上看,一次函数与反比例函数的交点由k值的符号来决定.
①k值同号,两个函数必有两个交点;
②k值异号,两个函数可无交点,可有一个交点,可有两个交点;
2)从计算上看,一次函数与反比例函数的交点主要取决于两函数所组成的方程组的解的情况.
解题时,一定要灵活运用一次函数与反比例函数的知识,并结合图象分析、解答问题.
1.(2022·四川德阳·统考中考真题)一次函数y=ax+1与反比例函数y=−ax在同一坐标系中的大致图象是( )
A.B.C.D.
【答案】B
【分析】A选项可以根据一次函数与y轴交点判断,其他选项根据图象判断a的符号,看一次函数和反比例函数判断出a的符号是否一致;
【详解】一次函数与y轴交点为(0,1),A选项中一次函数与y轴交于负半轴,故错误;
B选项中,根据一次函数y随x增大而减小可判断a<0,反比例函数过一、三象限,则-a>0,即a<0,两者一致,故B选项正确;
C选项中,根据一次函数y随x增大而增大可判断a>0,反比例函数过一、三象限,则-a>0,即a<0,两者矛盾,故C选项错误;
D选项中,根据一次函数y随x增大而减小可判断a<0,反比例函数过二、四象限,则-a<0,即a>0,两者矛盾,故D选项错误;
故选:B.
【点睛】本题考查了一次函数、反比例函数图象共存问题,解决此类题目要熟练掌握一次函数、反比例函数图象与系数的关系.
2.(2022·四川攀枝花·统考中考真题)如图,正比例函数y=k1x与反比例函数y=k2x的图像交于A(1,m)、B两点,当k1x≤k2x时,x的取值范围是( )
A.−1≤x<0或x≥1B.x≤−1或0
【分析】先根据反比例函数图像的对称点求出点B的坐标,然后根据k1x≤k2x的解集即为反比例函数在一次函数上方的部分可得答案.
【详解】解析:∵正比例函数y=k1x与反比例函数y=k2x的图像交于A(1,m)、B两点,
∴B(−1,−m),
由图像可知,当k1x≤k2x时,x的取值范围是−1≤x<0或x≥1,
故选:A.
【点睛】本题考查了一次函数与反比例函数的交点问题,根据反比例函数的对称性得出点B的坐标的坐标是解本题的关键.
3.(2023·四川遂宁·统考中考真题)如图,一次函数y=k1x+b的图像与反比例函数y=k2x的图像交于A−4,1,Bm,4两点.(k1,k2,b为常数)
(1)求一次函数和反比例函数的解析式;
(2)根据图像直接写出不等式k1x+b>k2x的解集;
(3)P为y轴上一点,若△PAB的面积为3,求P点的坐标.
【答案】(1)y=x+5;y=−4x
(2)−4
(3)0,3或(0,7).
【分析】(1)利用待定系数法即可求出函数解析式;
(2)根据图像位置关系即可得解;
(3)设P0,m,当点P在直线下方时,画出图形,根据S△PAB=S△PDA+S△PDB关系列方程,然后解方程即可得解,同理,当点P在直线上方时,画出图形,根据S△PAB=S△PAN−S△PBM−S梯形ANMB列方程求解即可.
【详解】(1)解:将点A−4,1代入y=k2x得1=k2−4,
∴k2=−4,
∴反比例函数的解析式为y=−4x;
将点Bm,4代入y=−4x得4=−4m,
∴m=−1,
将点A−4,1、B−1,4分别代入y=k1x+b得1=−4k1+b4=−k1+b,
解得k1=1b=5,
∴一次函数的解析式为y=x+5;
(2)根据图像可知,当−4
∴不等式k1x+b>k2x的解集为−4
(3)①如图过点P作x轴平行线l与AB交于点D,分别过点A,B作直线l垂线,垂足分别为点C、E,
设P0,m,则Dm−5,m,
∴PD=5−m,
则S△PAB=S△PDA+S△PDB,
=12PD⋅CA+12PD⋅BE,
=12PDBE+CA,
=32PD,
=325−m,
∵△PAB的面积为3,
∴325−m=3,
∴m=3,
即P点的坐标为0,3.
②如图,过A作AN⊥y轴于点N,过B作BM⊥y轴于点M,设P(0,m),
由(1)得:A(−4,1),B(1,4),
∴M(0,4),N(0,1),
∴PM=m−4,PN=m−1,MN=3,
则S△PAB=S△PAN−S△PBM−S梯形ANMB
=12AN·PN−12BM·PM−12(BM+AN)·MN
=12×4×(m−1)−12×1×(m−4)−12(1+4)×3
=2m−2−12m+2−152,
=32m−152=3,
∴m=7,
即P点的坐标为(0,7),
综上所述:P(0,3)或(0,7).
【点睛】本题考查反比例函数与一次函数综合、待定系数法求函数解析式、利用图像解不等式、坐标与图形等知识,掌握反比例函数与一次函数图像与性质是解题关键.
题型09 反比例函数与几何综合
解反比例函数与几何图形的综合题,一般先设出几何图形中的未知数,然后结合函数的图像用含未知数的式子表示出几何图形与图像的交点坐标,再由函数解析式及几何图形的性质写出含未知数及待求字母系数的当成(组),解方程(组)即可得所求几何图形的未知量或函数解析式中待定字母的值.这类型的题目主要包括反比例函数与三角形的综合、反比例函数与四边形(平行四边形、矩形、菱形)的综合、反比例函数与正方形的综合、反比例函数与圆的综合等四种题型.
1.(2022·江苏宿迁·统考中考真题)如图,点A在反比例函数y=2xx>0的图像上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1B.2C.22D.4
【答案】C
【分析】如图,过A作AM∥x轴,交y轴于M,过B作BD⊥x轴,垂足为D,交MA于H,则∠OMA=∠AHB=90°, 证明△AOM≌△BAH, 可得OM=AH,AM=BH, 设Am,2m, 则AM=m,OM=2m,MH=m+2m,BD=2m−m, 可得 Bm+2m,2m−m, 再利用勾股定理建立函数关系式,结合完全平方公式的变形可得答案.
【详解】解:如图,过A作AM∥x轴,交y轴于M,过B作BD⊥x轴,垂足为D,交MA于H,则∠OMA=∠AHB=90°,
∴∠MOA+∠MAO=90°,
∵AO=AB,AO⊥AB,
∴∠MAO+∠BAH=90°,
∴∠MOA=∠BAH,
∴△AOM≌△BAH,
∴OM=AH,AM=BH,
设Am,2m, 则AM=m,OM=2m,MH=m+2m,BD=2m−m,
∴ Bm+2m,2m−m,
∴OB=m+2m2+2m−m2=2m2+8m2,
∵m>0, 而当a>0,b>0时,则a+b≥2ab,
∴2m2+8m2≥22m2×8m2=8,
∴2m2+8m2的最小值是8,
∴OB的最小值是8=22.
故选:C.
【点睛】本题考查的是等腰直角三角形的性质,全等三角形的判定与性质,反比例函数的性质,完全平方公式的变形应用,勾股定理的应用,掌握“a2+b2≥2ab的变形公式”是解本题的关键.
2.(2022·江西·统考中考真题)已知点A在反比例函数y=12x(x>0)的图象上,点B在x轴正半轴上,若△OAB为等腰三角形,且腰长为5,则AB的长为 .
【答案】5或25或10
【分析】因为等腰三角形的腰不确定,所以分三种情况分别计算即可.
【详解】解:①当AO=AB时,AB=5;
②当AB=BO时,AB=5;
③当OA=OB时,则OB=5,B(5,0),
设A(a,12a)(a>0),
∵OA=5,
∴a2+(12a)2=5,
解得:a1=3,a2=4,
∴A(3,4)或(4,3),
∴AB=(3−5)2+42=25或AB=(4−5)2+32=10;
综上所述,AB的长为5或25或10.
故答案为:5或25或10.
【点睛】本题考查了等腰三角形的性质,反比例函数图象上点的坐标特征,考查分类讨论的思想,当时,求出点的坐标是解题的关键.
3.(2023·安徽·统考中考真题)如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=kx(k>0)的图象经过斜边OB的中点C.
(1)k= ;
(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2−BD2的值为 .
【答案】 3 4
【分析】(1)根据已知条件得出A,B的坐标,根据直角三角形斜边上的中线等于斜边的得出C的坐标,进而即可求解;
(2)根据题意,求得直线AC,BD,联立BD与反比例函数解析式,得出D的坐标,进而根据两点距离公式求得OB2,BD2,进而即可求解.
【详解】解:(1)∵AB=2,∠AOB=30°,∠OAB=90°,
∴OA=23,OB=2AB=4
∴A23,0,B23,2,
∵C是OB的中点,
∴C3,1,
∵反比例函数y=kx(k>0)的图象经过斜边OB的中点C.
∴k=3;
∴反比例数解析式为y=3x
故答案为:3;
(2)∵A23,0,C3,1
设直线AC的解析式为y=kx+b
∴0=23k+b1=3k+b
解得:k=−33b=2
∴直线AC的解析式为y=−33x+2,
∵DB∥AC,
设直线BD的解析式为y=−33x+b,将点B23,2代入并解得b=4,
∴直线BD的解析式为y=−33x+4,
∵反比例数解析式为y=3x
联立y=−33x+4y=3x
解得:x=23+3y=2−3或x=23−3y=2+3
当x=23+3y=2−3时, BD2=23+3−232+2−2+32=9+3=12
当x=23−3y=2+3时, BD2=23−23+32+2+3−22=9+3=12
OB2=232+22=16
∴OB2−BD2 =4,
故答案为:4.
【点睛】本题考查了反比例函数与几何图形,反比例函数与一次函数交点问题,熟练掌握反比例函数的性质是解题的关键.
4.(2023·浙江宁波·统考中考真题)如图,点A,B分别在函数y=ax(a>0)图象的两支上(A在第一象限),连接AB交x轴于点C.点D,E在函数y=bx(b<0,x<0)图象上,AE∥x轴,BD∥y轴,连接DE,BE.若AC=2BC,△ABE的面积为9,四边形ABDE的面积为14,则a−b的值为 ,a的值为 .
【答案】 12 9
【分析】如图,延长BD,AE交于点Q,BD与x轴交于点K,而AE∥x轴,BD∥y轴,可得∠Q=90°,△BDE的面积是5,设Am,am,Bn,an,则Qn,am,Dn,bn,Ebma,am,利用面积可得b−abm−an=10na①,n−ma−b=18n②,由OK∥AQ,AC=2BC,可得QK=2BK,可得n=−2m③,再利用方程思想解题即可.
【详解】解:如图,延长BD,AE交于点Q,BD与x轴交于点K,而AE∥x轴,BD∥y轴,
∴∠Q=90°,
∵△ABE的面积为9,四边形ABDE的面积为14,
∴△BDE的面积是5,
设Am,am,Bn,an,
∴Qn,am,Dn,bn,Ebma,am
∴BD=bn−an,EQ=bma−n,AE=m−bma,BQ=am−an,
∴12bn−anbma−n=5,12m−bmaam−an=9,
整理得:b−abm−an=10na①,n−ma−b=18n②,
∵OK∥AQ,AC=2BC,
∴BKQK=BCAC=12,
∴QK=2BK,
∴am=2×−an,则n=−2m③,
把③代入②得:−3ma−b=18×−2m,
∴a−b=12,即b=a−12④,
把③代入①得:b−ab+2a=−20a⑤,
把④代入⑤得:a=9;
故答案为:12;9
【点睛】本题考查的是反比例函数的几何应用,平行线分线段成比例的应用,坐标与图形面积,熟练的利用方程思想解题是关键.
5.(2021·河南·统考中考真题)如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数y=kx的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B.
(1)求反比例函数的解析式;
(2)求图中阴影部分的面积.
【答案】(1)反比例函数的解析式为y=2x;(2)阴影部分的面积为8.
【分析】(1)利用待定系数法即可求解;
(2)根据点B是小正方形在第一象限的一个点,知其横纵坐标相等,求得点B的坐标,继而求得小正方形的面积,再求得大正方形的面积,从而求得阴影部分的面积.
【详解】解:(1)由题意,点A(1,2)在反比例函数y=kx的图象上,
∴k=1×2=2,
∴反比例函数的解析式为y=2x;
(2)点B是小正方形在第一象限的一个点,由题意知其横纵坐标相等,
设B(a,a),则有k=a×a=2,
∴a=2,即B(2,2),
∴小正方形的边长为22,
∴小正方形的面积为(22)2=8,
大正方形经过点A(1,2),则大正方形的边长为4,
∴大正方形的面积为42=16,
∴图中阴影部分的面积为16-8=8.
【点睛】本题考查了反比例函数与几何的综合,反比例函数图象上点的坐标特征,解题的关键是根据点的坐标,利用待定系数法求出反比例函数解析式.
题型10 求二次函数的解析式
求二次函数解析式的一般方法:
1)一般式y=ax2+bx+c.代入三个点的坐标列出关于a, b, c的方程组,并求出a, b, c,就可以写出二次函数的解析式.
2)顶点式y=a(x-h)2+k.根据顶坐标点(h,k),可设顶点式y=a(x-h)2+k,再将另一点的坐标代入,即可求出a的值,从而写出二次函数的解析式.
3)交点式y=a(x-x1)(x-x2).当抛物线与x轴的两个交点为(x1,0)、(x2,0)时,可设y=a(x-x1)(x-x2),再将另一点的坐标代入即可求出a的值,从而写出二次函数的解析式.
1.(2023·江苏泰州·统考中考真题)函数y与自变量x的部分对应值如表所示,则下列函数表达式中,符合表中对应关系的可能是( )
A.y=ax+b(a<0)B.y=ax(a<0)
C.y=ax2+bx+c(a>0)D.y=ax2+bx+c(a<0)
【答案】C
【分析】根据反比例函数的坐标特征,一次函数的性质,二次函数的坐标特征即可判断.
【详解】解:A、若直线y=ax+b过点1,4,2,2,
则a+b=42a+b=2,解得a=−2b=6,
所以y=−2x+6,
当x=4时,y=−2,故4,1不在直线y=ax+b上,故A不合题意;
B、由表格可知,y与x的每一组对应值的积是定值为4,所以y是x的反比例函数,a=4>0,不合题意;
C、把表格中的函数y与自变量x的对应值代入y=ax2+bx+c得
a+b+c=44a+2b+c=216a+4b+c=1,解得a=12b=−72c=7,符合题意;
D、由C可知,不合题意.
故选:C.
【点睛】主要考查反比例函数、一次函数以及二次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.
2.(2021·广东广州·统考中考真题)抛物线y=ax2+bx+c经过点−1,0、3,0,且与y轴交于点0,−5,则当x=2时,y的值为( )
A.−5B.−3C.−1D.5
【答案】A
【分析】解法一:先利用待定系数法求出抛物线解析式,再求函数值即可.
解法二:利用二次函数图象的对称性可知:x=2和x=0对应的函数值相等,从而得解.
【详解】解:∵抛物线y=ax2+bx+c经过点−1,0、3,0,且与y轴交于点0,−5,
∴c=−5a−b+c=09a+3b+c=0,
解方程组得c=−5a=53b=−103,
∴抛物线解析式为y=53x2−103x−5,
当x=2时,y=53×4−103×2−5=−5.
故选择A.
解法二:抛物线y=ax2+bx+c经过点−1,0、3,0,
∴抛物线的对称轴为:x=−1+32=1,
又∵0+22=1,
∴x=2和x=0的函数值相等,即均为−5,
故选择A.
【点睛】本题考查待定系数法求抛物线解析式,和函数值,掌握系数法求抛物线解析式方法和函数值求法是解题关键.同时利用数形结合思想和对称性解题会起到事半功倍的效果.
3.(2023·浙江宁波·统考中考真题)如图,已知二次函数y=x2+bx+c图象经过点A(1,−2)和B(0,−5).
(1)求该二次函数的表达式及图象的顶点坐标.
(2)当y≤−2时,请根据图象直接写出x的取值范围.
【答案】(1)y=x2+2x−5,顶点坐标为−1,−6;
(2)−3≤x≤1
【分析】(1)把A(1,−2)和B(0,−5)代入y=x2+bx+c,建立方程组求解解析式即可,再把解析式化为顶点式,可得顶点坐标;
(2)把y=−2代入函数解析式求解x的值,再利用函数图象可得y≤−2时x的取值范围.
【详解】(1)解:∵二次函数y=x2+bx+c图象经过点A(1,−2)和B(0,−5).
∴c=−51+b+c=−2,解得:b=2c=−5,
∴抛物线为y=x2+2x−5=x+12−6,
∴顶点坐标为:−1,−6;
(2)当y=−2时,x+12−6=−2,
∴x+12=4
解得:x1=1,x2=−3,
如图,当y≤−2时,
∴−3≤x≤1.
【点睛】本题考查的是利用待定系数法求解二次函数的解析式,二次函数的顶点坐标,利用图象法解不等式,熟练的运用数形结合的方法解题是关键.
题型11 二次函数的图象与性质
1.(2023·辽宁大连·统考中考真题)已知抛物线y=x2−2x−1,则当0≤x≤3时,函数的最大值为( )
A.−2B.−1C.0D.2
【答案】D
【分析】把抛物线y=x2−2x−1化为顶点式,得到对称轴为x=1,当x=1时,函数的最小值为−2,再分别求出x=0和x=3时的函数值,即可得到答案.
【详解】解:∵y=x2−2x−1=x−12−2,
∴对称轴为x=1,当x=1时,函数的最小值为−2,
当x=0时,y=x2−2x−1=−1,当x=3时,y=32−2×3−1=2,
∴当0≤x≤3时,函数的最大值为2,
故选:D
【点睛】此题考查了二次函数的最值,熟练掌握二次函数的性质是解题的关键.
2.(2023·甘肃兰州·统考中考真题)已知二次函数y=−3x−22−3,下列说法正确的是( )
A.对称轴为x=−2B.顶点坐标为2,3C.函数的最大值是-3D.函数的最小值是-3
【答案】C
【分析】根据二次函数的图象及性质进行判断即可.
【详解】二次函数y=−3x−22−3的对称轴为x=2,顶点坐标为2,−3
∵−3<0
∴二次函数图象开口向下,函数有最大值,为y=−3
∴A、B、D选项错误,C选项正确
故选:C
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数图象和性质是解题的关键.
3.(2023·四川甘孜·统考中考真题)下列关于二次函数y=(x−2)2−3的说法正确的是( )
A.图象是一条开口向下的抛物线B.图象与x轴没有交点
C.当x<2时,y随x增大而增大D.图象的顶点坐标是(2,−3)
【答案】D
【分析】由二次函数解析式可得抛物线开口方向、对称轴、顶点坐标,与x轴的交点个数,由此解答即可.
【详解】解:A、∵a=1>0,图象的开口向上,故此选项不符合题意;
B、∵ y=(x−2)2−3=x2−4x+1,
∴ Δ=(−4)2−4×1×1=12>0,
即图象与x轴有两个交点,
故此选项不符合题意;
C、∵抛物线开口向上,对称轴为直线x=2,
∴当x<2时,y随x增大而减小,
故此选项不符合题意;
D、∵ y=(x−2)2−3,
∴图象的顶点坐标是(2,−3),
故此选项符合题意;
故选:D.
【点睛】本题考查了二次函数的图象性质,解题的关键是掌握二次函数图象与系数的关系.
4.(2022·湖北荆门·统考中考真题)抛物线y=x2+3上有两点A(x1,y1),B(x2,y2),若y1<y2,则下列结论正确的是( )
A.0≤x1<x2B.x2<x1≤0
C.x2<x1≤0或0≤x1<x2D.以上都不对
【答案】D
【分析】根据二次函数图象及性质,即可判定.
【详解】∵抛物线y=x2+3开口向上,在其图象上有两点A(x1,y1),B(x2,y2),且y1<y2,
∴|x1|<|x2|,
∴0≤x1<x2,或x2<x1≤0,或x2
【点睛】本题考查了二次函数的图象及性质,熟练掌握和运用二次函数的图象及性质是解决本题的关键.
题型12 二次函数的图象与各系数符号
一、二次函数y=ax2+bx+c(a≠0)的图象与a,b,c的关系
二、二次函数y=ax2+bx+c(a≠0)的常见结论
1.(2022·四川成都·统考中考真题)如图,二次函数y=ax2+bx+c的图像与x轴相交于A(−1,0),B两点,对称轴是直线x=1,下列说法正确的是( )
A.a>0B.当x>−1时,y的值随x值的增大而增大
C.点B的坐标为(4,0)D.4a+2b+c>0
【答案】D
【分析】结合二次函数图像与性质,根据条件与图像,逐项判定即可.
【详解】解:A、根据图像可知抛物线开口向下,即a<0,故该选项不符合题意;
B、根据图像开口向下,对称轴为x=1,当x>1,y随x的增大而减小;当x<1,y随x的增大而增大,故当−1
C、根据二次函数y=ax2+bx+c的图像与x轴相交于A(−1,0),B两点,对称轴是直线x=1,可得对称轴x=xB+(−1)2=1,解得xB=3,即B(3,0),故该选项不符合题意;
D、根据B(3,0)可知,当x=2时,y=4a+2b+c>0,故该选项符合题意;
故选:D.
【点睛】本题考查二次函数的图像与性质,根据图像得到抛物线开口向下,根据对称轴以及抛物线与x轴交点A(−1,0)得到B(3,0)是解决问题的关键.
2.(2023·湖南娄底·统考中考真题)已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc<0;②4a−2b+c>0;③a−b>mam+b(m为任意实数);④若点−3,y1和点3,y2在该图象上,则y1>y2.其中正确的结论是( )
A.①②B.①④C.②③D.②④
【答案】D
【分析】由抛物线的开口向下,与y轴交于正半轴,对称轴在y轴的左边,可得a<0,c>0, b<0,故①不符合题意;当x=0与x=−2时的函数值相等,可得4a−2b+c=c>0,故②符合题意;当x=−1时函数值最大,可得a−b≥mam+b,故③不符合题意;由点−3,y1和点3,y2在该图象上,而3−−1=4>−1−−3=2,且离抛物线的对称轴越远的点的函数值越小,可得④符合题意.
【详解】解:∵抛物线的开口向下,与y轴交于正半轴,对称轴在y轴的左边,
∴a<0,c>0,x=−b2a<0,
∴b<0,
∴abc>0,故①不符合题意;
∵对称轴为直线x=−1,
∴当x=0与x=−2时的函数值相等,
∴4a−2b+c=c>0,故②符合题意;
∵当x=−1时函数值最大,
∴a−b+c≥am2+bm+c,
∴a−b≥mam+b;故③不符合题意;
∵点−3,y1和点3,y2在该图象上,
而3−−1=4>−1−−3=2,且离抛物线的对称轴越远的点的函数值越小,
∴y1>y2.故④符合题意;
故选:D.
【点睛】本题考查的是二次函数的图象与性质,熟记二次函数的开口方向,与y轴的交点坐标,对称轴方程,增减性的判定,函数的最值这些知识点是解本题的关键.
3.(2023·四川广安·统考中考真题)如图所示,二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象与x轴交于点A−3,0,B1,0.有下列结论:①abc>0;②若点−2,y1和−0.5,y2均在抛物线上,则y1
A.1个B.2个C.3个D.4个
【答案】C
【分析】根据二次函数图像的性质、二次函数图像与系数的关系以及与x轴交点问题逐项分析判断即可.
【详解】解:由图可知,二次函数开口方向向下,与y轴正半轴交于一点,
∴a<0,c>0.
∵−b2a<0,
∴b<0.
∴abc>0.
故①正确.
∵ A−3,0,B1,0是关于二次函数对称轴对称,
∴−b2a=−1.
∴−2,y1在对称轴的左边,−0.5,y2在对称轴的右边,如图所示,
∴y1
∵图象与x轴交于点A−3,0,B1,0,
∴9a−3b+c=0,a+b+c=0.
∴10a−2b+2c=0.
∴5a−b+c=0.
故③正确.
∵ −b2a=−1,
∴b=2a.
当x=1时,y=0,
∴a+b+c=0.
∴3a+c=0,
∴c=−3a,
∴4a+c=4a−3a=a<0.
故④不正确.
综上所述,正确的有①②③.
故选:C.
【点睛】本题考查了二次函数图像与系数之间的关系,解题的关键在于通过图像判断对称轴,开口方向以及与y轴交点.
4.(2023·四川达州·统考中考真题)如图,拋物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.下列五个结论:①abc>0;②2a+b=0;③4a+2b+c>0;④am2+bm>a+b;⑤3a+c>0.其中正确的有( )
A.4个B.3个C.2个D.1个
【答案】B
【分析】由抛物线的开口方向、与y轴交点以及对称轴的位置可判断a、b、c的符号,由此可判断①正确;由抛物线的对称轴为x=1,得到−b2a=1,即可判断②;可知x=2时和x=0时的y值相等可判断③正确;由图知x=1时二次函数有最小值,可判断④错误;由抛物线的对称轴为x=1可得b=−2a,因此y=ax2−2ax+c,根据图像可判断⑤正确.
【详解】①∵抛物线的开口向上,
∴a>0.
∵抛物线与y轴交点在y轴的负半轴上,
∴c<0.
由−b2a>0得,b<0,
∴abc>0,
故①正确;
②∵抛物线的对称轴为x=1,
∴ −b2a=1,
∴ b=−2a,
∴ 2a+b=0,故②正确;
③由抛物线的对称轴为x=1,可知x=2时和x=0时的y值相等.
由图知x=0时,y<0,
∴x=2时,y<0.
即4a+2b+c<0.
故③错误;
④由图知x=1时二次函数有最小值,
∴a+b+c≤am2+bm+c,
∴a+b≤am2+bm,
a+b≤m(ax+b),
故④错误;
⑤由抛物线的对称轴为x=1可得−b2a=1,
∴b=−2a,
∴y=ax2−2ax+c,
当x=−1时,y=a+2a+c=3a+c.
由图知x=−1时y>0,
∴3a+c>0.
故⑤正确.
综上所述:正确的是①②⑤,有3个,
故选:B.
【点睛】本题主要考查了二次函数的图像与系数的关系,二次函数的对称轴及顶点位置.熟练掌握二次函数图像的性质及数形结合是解题的关键.
题型13 二次函数与一次函数、反比例函数综合判断
1.(2021·广东深圳·统考中考真题)二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
【答案】A
【分析】先分析二次函数y=ax2+bx+1的图像的开口方向即对称轴位置,而一次函数y=2ax+b的图像恒过定点(−b2a,0),即可得出正确选项.
【详解】二次函数y=ax2+bx+1的对称轴为x=−b2a,一次函数y=2ax+b的图像恒过定点(−b2a,0),所以一次函数的图像与二次函数的对称轴的交点为(−b2a,0),只有A选项符合题意.
故选A.
【点睛】本题考查了二次函数的图像与性质、一次函数的图像与性质,解决本题的关键是能推出一次函数y=2ax+b的图像恒过定点(−b2a,0),本题蕴含了数形结合的思想方法等.
2.(2021·江西·中考真题)在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )
A.B.C.D.
【答案】D
【分析】根据二次函数y=ax2与一次函数y=bx+c的图象可知a>0,b>0,c<0,从而判断出二次函数y=ax2+bx+c的图象.
【详解】解:∵二次函数y=ax2的图象开口向上,
∴a>0,
∵次函数y=bx+c的图象经过一、三、四象限,
∴b>0,c<0,
对于二次函数y=ax2+bx+c的图象,
∵a>0,开口向上,排除A、B选项;
∵a>0,b>0,
∴对称轴x=−b2a<0,
∴D选项符合题意;
故选:D.
【点睛】本题考查了一次函数的图象以及二次函数的图象,根据二次函数的图象和一次函数图象经过的象限,找出a>0,b>0,c<0是解题的关键.
3.(2022·山东菏泽·统考中考真题)根据如图所示的二次函数y=ax2+bx+c的图象,判断反比例函数y=ax与一次函数y=bx+c的图象大致是( )
A.B.C.D.
【答案】A
【分析】先根据二次函数的图象,确定a、b、c的符号,再根据a、b、c的符号判断反比例函数y=ax与一次函数y=bx+c的图象经过的象限即可.
【详解】解:由二次函数图象可知a>0,c<0,
由对称轴x=−b2a>0,可知b<0,
所以反比例函数y=ax的图象在一、三象限,
一次函数y=bx+c经过二、三、四象限.
故选:A.
【点睛】本题主要考查二次函数图象的性质、一次函数的图象的性质、反比例函数图象的性质,关键在于通过二次函数图象推出a、b、c的取值范围.
4.(2021·山东青岛·统考中考真题)已知反比例函数y=bx的图象如图所示,则一次函数y=cx+a和二次函数y=ax2+bx+c在同一直角坐标系中的图象可能是( )
A.B.C.D.
【答案】D
【分析】根据反比例函数的图象得出b<0,逐一分析四个选项,根据二次函数图象的开口以及对称轴与y轴的关系,抛物线与y轴的交点,即可得出a、b、c的正负,由此即可得出一次函数图象经过的象限,再与函数图象进行对比即可得出结论.
【详解】解:∵反比例函数的图象在二、四象限,
∴b<0,
A、∵二次函数图象开口向上,对称轴在y轴右侧,交y轴的负半轴,
∴a>0,b<0,c<0,
∴一次函数图象应该过第一、二、四象限,A错误;
B、∵二次函数图象开口向下,对称轴在y轴右侧,
∴a<0,b>0,
∴与b<0矛盾,B错误;
C、∵二次函数图象开口向下,对称轴在y轴右侧,
∴a<0,b>0,
∴与b<0矛盾,C错误;
D、∵二次函数图象开口向上,对称轴在y轴右侧,交y轴的负半轴,
∴a<0,b<0,c<0,
∴一次函数图象应该过第一、二、四象限,D正确.
故选:D.
【点睛】本题主要考查了一次函数、反比例函数、二次函数的图象与性质,根据函数图象与系数的关系进行判断是解题的关键,同时考查了数形结合的思想.
题型14 求二次函数最值
备注:自变量的取值为x1≤x≤x2时,且二次项系数a<0的最值情况请自行推导.
1. 抛物线的增减性问题,由a的正负和对称轴同时确定,单一的直接说,y随x 的增大而增大(或减小) 是不对的,必须附加一定的自变量x 取值范围.
2. 抛物线在平移的过程中,a的值不发生变化,变化的只是顶点的位置,且与平移方向有关.
3. 涉及抛物线的平移时,首先将表达式转化为顶点式y=a(x-h)2+k的形式,因为二次函数平移遵循“上加下减,左加右减”的原则,因此可以直接由解析式中常数的加或减求出变化后的解析式.
1.(2023·山东泰安·统考中考真题)二次函数y=−x2−3x+4的最大值是 .
【答案】254
【分析】利用配方法把二次函数一般式化为顶点式,即可求解.
【详解】解:利用配方法,将一般式化成顶点式:
y=−x2−3x+4 =−(x+32)2+254
∵二次函数开口向下,
∴顶点处取最大值,
即当x=−32时,最大值为254.
故答案为:254.
【点睛】本题考查二次函数的相关知识.将一般式化为顶点式,顶点处取到最值.其中配方法是解决问题的关键,也是易错点.
2.(2023·陕西·统考中考真题)在平面直角坐标系中,二次函数y=x2+mx+m2−m(m为常数)的图像经过点(0,6),其对称轴在y轴左侧,则该二次函数有( )
A.最大值5B.最大值154C.最小值5D.最小值154
【答案】D
【分析】将(0,6)代入二次函数解析式,进而得出m的值,再利用对称轴在y轴左侧,得出m=3,再利用二次函数的顶点式即可求出二次函数最值.
【详解】解:将(0,6)代入二次函数解析式y=x2+mx+m2−m得:6=m2−m,解得:m1=3,m2=−2,
∵二次函数y=x2+mx+m2−m,对称轴在y轴左侧,即x=−b2a=−m2<0,
∴m>0,
∴m=3,
∴y=x2+3x+6=x+322+154,
∴当x=−23时,二次函数有最小值,最小值为154,
故选:D.
【点睛】此题主要考查了二次函数的性质以及二次函数的最值,正确得出m的值是解题关键.
3.(2022·内蒙古包头·中考真题)已知实数a,b满足b−a=1,则代数式a2+2b−6a+7的最小值等于( )
A.5B.4C.3D.2
【答案】A
【分析】由已知得b=a+1,代入代数式即得a2-4a+9变形为(a-2)2+5,再根据二次函数性质求解.
【详解】解:∵b-a=1,
∴b=a+1,
∴a2+2b-6a+7
=a2+2(a+1)-6a+7
=a2-4a+9
=(a-2)2+5,
∵(a-2)2≥0,
∴当a=2时,代数式a2+2b-6a+7有最小值,最小值为5,
故选:A.
【点睛】本题考查二次函数的最值,通过变形将代数式化成(a-2)2+5是解题的关键.
4.(2022·浙江绍兴·统考中考真题)已知函数y=−x2+bx+c(b,c为常数)的图象经过点(0,﹣3),(﹣6,﹣3).
(1)求b,c的值.
(2)当﹣4≤x≤0时,求y的最大值.
(3)当m≤x≤0时,若y的最大值与最小值之和为2,求m的值.
【答案】(1)b=-6,c=-3
(2)x=-3时,y有最大值为6
(3)m=-2或−3−10
【分析】(1)把(0,-3),(-6,-3)代入y=−x2+bx+c,即可求解;
(2)先求出抛物线的顶点坐标为(-3,6),再由-4≤x≤0,可得当x=-3时,y有最大值,即可求解;
(3)由(2)得当x>-3时,y随x的增大而减小;当x≤-3时,y随x的增大而增大,然后分两种情况:当-3<m≤0时,当m≤-3时,即可求解.
【详解】(1)解:把(0,-3),(-6,-3)代入y=−x2+bx+c,得∶
c=−3−36−6b+c=−3,解得:b=−6c=−3;
(2)解:由(1)得:该函数解析式为y=−x2−6x−3=−(x+3)2+6,
∴抛物线的顶点坐标为(-3,6),
∵-1<0
∴抛物线开口向下,
又∵-4≤x≤0,
∴当x=-3时,y有最大值为6.
(3)解:由(2)得:抛物线的对称轴为直线x=-3,
∴当x>-3时,y随x的增大而减小;当x≤-3时,y随x的增大而增大,
①当-3<m≤0时,
当x=0时,y有最小值为-3,
当x=m时,y有最大值为−m2−6m−3,
∴−m2−6m−3+(-3)=2,
∴m=-2或m=-4(舍去).
②当m≤-3时,
当x=-3时,y有最大值为6,
∵y的最大值与最小值之和为2,
∴y最小值为-4,
∴−(m+3)2+6=-4,
∴m=−3−10或m=−3+10(舍去).
综上所述,m=-2或−3−10.
【点睛】本题主要考查了二次函数的图象和性质,熟练掌握二次函数的图象和性质,并利用分类讨论思想解答是解题的关键.
题型15 二次函数的平移问题
1.(2023·江苏徐州·统考中考真题)在平面直角坐标系中,将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为( )
A.y=(x+3)2+2B.y=(x−1)2+2C.y=(x−1)2+4D.y=(x+3)2+4
【答案】B
【分析】根据二次函数图象的平移“左加右减,上加下减”可进行求解.
【详解】解:由二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得拋物线对应的函数表达式为y=(x−1)2+2;
故选B.
【点睛】本题主要考查二次函数图象的平移,熟练掌握二次函数图象的平移是解题的关键.
2.(2021·江苏苏州·统考中考真题)已知抛物线y=x2+kx−k2的对称轴在y轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则k的值是( )
A.−5或2B.−5C.2D.−2
【答案】B
【分析】根据二次函数图象左加右减,上加下减的平移规律进行解答即可.
【详解】解:函数y=x2+kx−k2向右平移3个单位,得:y=(x−3)2+k(x−3)−k2;
再向上平移1个单位,得:y=(x−3)2+k(x−3)−k2+1,
∵得到的抛物线正好经过坐标原点
∴0=(0−3)2+k(0−3)−k2+1即k2+3k−10=0
解得:k=−5或k=2
∵抛物线y=x2+kx−k2的对称轴在y轴右侧
∴x=−k2>0
∴k<0
∴k=−5
故选:B.
【点睛】此题主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.
3.(2021·广东·统考中考真题)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .
【答案】y=2x2+4x
【分析】直接根据“上加下减,左加右减”进行计算即可.
【详解】解:抛物线y=2x2+1向左平移1个单位长度,
再向下平移3个单位长度,
得到的抛物线的解析式为:y=2(x+1)2+1−3,
即:y=2x2+4x
故答案为:y=2x2+4x.
【点睛】本题主要考查函数图像的平移,熟记函数图像的平移方式“上加下减,左加右减”是解题的关键
一、一次函数
二、反比例系数k的几何意义
1.一点一垂线
【模型结论】反比例函数图象上一点关于坐标轴的垂线、与另一坐标轴上一点(含原点)围成的三角形面积为12k.
【拓展一】 【拓展二】 【拓展三】(前提:OA=AC)
结论:S△AOB=S△COD S△AOE=S四边形CEBD S△AOC=k
2.一点两垂线
【模型结论】反比例函数图象上一点与坐标轴的两条垂线围成的矩形面积为k.
【拓展一】 【拓展二】 【拓展三】
结论:S矩形ABOE=S矩形CDOF S矩形AEFG=S矩形CGBD S ▱ABCD=k
3.两点一垂线
【模型结论一】反比例函数与正比例函数图象的交点及由交点向坐标轴所作垂线围成的三角形面积等于|k|,
结论:S△ABC =2S△ABO =k
【模型结论二】反比例函数与一次函数图象的交点及坐标轴上任一点构成三角形的面积,等于坐标轴所分的两个三角形面积之和.
如左图,已知一次函数与反比例函数y=kx交于A、B两点,且一次函数与x轴交于点C,
则S△AOB=S△AOC+S△BOC=12c•|yA|+12c•|yB|=12c(|yA|+|yB|)
如右图,已知一次函数与反比例函数y=kx交于A、B两点,且一次函数与y轴交于点C,
则S△AOB=S△AOC+S△BOC=12c•|xA|+12c•|xB|=12c(|xA|+|xB|)
4.两点两垂线
【模型结论】反比例函数与正比例函数图象的交点及由交点向坐标轴所作两条垂线围成的图形面积等于2|k|
5.两点和原点
方法一:S△AOB=S△COD-S△AOC-S△BOD.【分割】
方法二:作AE⊥x轴于点E,交OB于点M,BF⊥x轴于点F,而S△OAM=S四边形MEFB,则S△AOB=S直角梯形AEFB.
方法三:S△AOB=S四边形COFD-S△AOC-S△BOF. 【补形】
方法四:S△AOB=S△AOD-S△BOD=12OD•(|yA|-|yB|)
方法五:S△AOB=S△BOC-S△AOC=12OC•(|xB|-|xA|)
【拓展】
方法一:当AD/AC(或BD/BF)=m时,则S四边形OADB=m|k|.
方法二:作AE⊥x轴于E,则S△OAB=S直角梯形AEFB(类型一).
6.两曲一平行
【模型讲解】两条双曲线上的两点的连线与一条(或两条)坐标轴平行,求这两点与原点或坐标轴上的点围成的图形面积,过这两点作坐标轴的垂线,结合k的几何意义求解.
类型一 两条双曲线的k值符号相同
结论:S阴影=|k1|-|k2| S阴影=12|k1|- 12|k2|
结论:S阴影=|k1|-|k2| S阴影=|k1|-|k2|- S直角梯形AFDE
类型二 两条双曲线的k值符号相同
结论:S△AOB=S△ACB=12(|k1|+|k2|) S阴影=|k1|+|k2|
三、二次函数
1. 二次函数的图象变换
1)二次函数的平移变换
2)二次函数图象的翻折与旋转
2. 二次函数的对称性问题
抛物线的对称性的应用,主要体现在:
1)求一个点关于对称轴对称的点的坐标;
2)已知抛物线上两个点关于对称轴对称,求其对称轴.
解此类题的主要根据:若抛物线上两个关于对称轴对称的点的坐标分别为(x1,y),(x2,y),则抛物线的对称轴可表示为直线x=x1+x22.
解题技巧:
1.抛物线上两点若关于直线,则这两点的纵坐标相同,横坐标与x=−b2a的差的绝对值相等;
2若二次函数与x轴有两个交点,则这两个交点关于直线x=−b2a对称;
3二次函数y=ax2+bx+c与y=ax2-bx+c的图象关于y轴对称;二次函数y=ax2+bx+c与y=-ax2-bx-c的图象于x轴对称.
1.(2023·海南三亚·统考二模)若点(−1,4)在反比例函数y=kx的图象上,则下列各点在此函数图象上的是( )
A.−14,1B.(−4,−1) C.14,2D.(−4,1)
【答案】D
【分析】本题考查利用待定系数法求反比例函数解析式和反比例函数图象上点的坐标特征.先利用待定系数法求出反比例函数解析式,再逐个选项判断即可.
【详解】解:将点(−1,4)代入反比例函数解析式,得:4=k−1,
解得:k=−4,
∴反比例函数解析式为:y=−4x.
当x=−14时,y=16,故−14,1不在反比例函数图象上,故A不符合题意;
当x=−4时,y=1,故(−4,−1)不在反比例函数图象上,(−4,1)在反比例函数图象上,故B不符合题意,D符合题意;
当x=14时,y=−16,故14,2不在反比例函数图象上,故C不符合题意.
故选:D.
2.(2023·山东青岛·校考模拟预测)函数y=2x+32+5的图像是由y=2x2( )得到
A.先向下平移5个单位,再向右平移3个单位B.先向上平移5个单位,再向左平移3个单位
C.先向上平移5个单位,再向右平移3个单位D.先向上平移5个单位,再向右平移3个单位
【答案】B
【分析】本题考查函数图像平移,根据函数图像平移法则:左加右减、上加下减,结合题中所给抛物线的顶点式直接按要求平移即可得到答案.
【详解】解:y=2x2先向上平移5个单位,再向左平移3个单位得到y=2x+32+5,
故选:B.
3.(2023·新疆乌鲁木齐·模拟预测)如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得不等式ax+b
【答案】A
【分析】本题考查了一次函数交点问题,根据函数图象写出一次函数y=ax+b的图象在一次函数y=kx图象的下方的自变量的取值范围即可求解.
【详解】∵由函数图象可知,当x>−4时一次函数y=ax+b的图象在一次函数y=kx图象的下方,
∴关于x的不等式ax+b
故选:A.
4.(2023·安徽·模拟预测)已知一次函数y=2x+3的图象经过点Pk,b,则关于x的一次函数y=kx+b(k,b为常数,且k≠0)的图象不可能是( )
A. B. C. D.
【答案】B
【分析】本题考查一次函数的性质及图象,熟练应用一次函数的性质是解答本题的关键.由函数经过点Pk,b,代入解析式求出函数经过定点−2,3,结合选项判断即可.
【详解】解:∵一次函数y=2x+3的图象经过点Pk,b,
∴b=2k+3,
∴y=kx+2k+3=kx+2+3,
∴对于任意实数k,恒有当x=−2时,y=3,
∴一次函数y=kx+b的图象经过定点−2,3.
观察可知只有B项图象不满足条件.
故选:B.
5.(2023·吉林长春·校考模拟预测)一块直角三角尺ABC按如图放置,顶点A的坐标为0,3,直角顶点C的坐标为−4,0,∠B=30°,反比例函数y=kx过点B,则k的值为( )
A.−43B.−73C.−213D.−283
【答案】D
【分析】本题考查反比例函数与几何的综合应用,解直角三角形,相似三角形的判定和性质.过点B作BD⊥x轴于点D,根据锐角三角函数得到tan30°=ACBC=33,证明△CDB∽△AOC,得到AOCD=OCBD=ACBC=33,求出CD=3,BD=43,进而求出点B的坐标,即可.解题的关键是求出点B的坐标.
【详解】解:过点B作BD⊥x轴于点D,则:∠BDC=90°,
∵顶点A的坐标为0,3,直角顶点C的坐标为−4,0,
∴OA=3,OC=4,
∵直角三角尺ABC,∠B=30°,∠ACB=90°,
∴tan30°=ACBC=33,
∵∠BDC=90°=∠BCA=∠AOC,
∴∠DBC=∠ACO=90°−∠BCD,
∴△CDB∽△AOC,
∴AOCD=OCBD=ACBC=33,即:3CD=4BD=ACBC=33,
∴CD=3,BD=43,
∴OD=OC+CD=7,
∴B−7,43,
∵反比例函数y=kx过点B,
∴k=−7×43=−283;
故选D.
6.(2023·四川成都·模拟预测)如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A,B两点,与y轴交于点C,OA=OC,对称轴为直线x=1,则下列结论:①abc<0;②a+12b+14c=0;③ac+b+1=0;④2+c是关于x的一元二次方程ax2+bx+c=0的一个根.其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】B
【分析】本题考查了抛物线与x轴交点及与二次函数图象与系数的关系,根据二次函数的开口方向,与y轴的交点,对称轴可知a<0,c>0,b=−2a>0,由此即可判断①②;再根据C0,c,OA=OC,得到A−c,0,即可推出ac−b+1=0,即可判断③;根据对称性求出B2+c,0,即可判断④.
【详解】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=−b2a=1,
∴b=−2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵点A到直线x=1的距离大于1,
∴点B到直线x=1的距离大于1,
即点B在2,0的右侧,
∴当x=2时,y>0,
即4a+2b+c>0,
∴a+12b+14c>0,所以②错误;
∵C0,c,OA=OC,
∴A−c,0,
∴ac2−bc+c=0,即ac−b+1=0,所以③错误;
∵点A与点B关于直线x=1对称,
∴B2+c,0,
∴2+c是关于x的一元二次方程ax2+bx+c=0的一个根,所以④正确.
故选:B.
7.(2023·广东清远·统考三模)抛物线y=ax2+bx+c的对称轴是直线x=−2,抛物线与x轴的一个交点在点−4,0和点−3,0之间,其部分图象如图所示,下列结论①4a−b=0;②a−b+c>0;③关于x的方程ax2+bx+c=2有两个不相等实数根;④当x>−2时,y随x增大而增大;⑤abc>0;⑥y的最小值为3.其中正确的个数是( )
A.2个B.3个C.4个D.5个
【答案】B
【分析】本题考查了y=ax²+bx+c的图象与性质,根据对称轴确定抛物线与x轴的另一个交点,补全图象是解题关键.
【详解】解:∵抛物线y=ax2+bx+c的对称轴是直线x=−2,
∴−b2a=−2,
∴b=4a,
即:4a−b=0,故①正确;
∵抛物线与x轴的一个交点在点−4,0和点−3,0之间,对称轴是直线x=−2,
∴抛物线与x轴的另一个交点在点−1,0和点0,0之间,
补全图象如下:
∴当x=−1时,y=a−b+c>0,故②正确;
由图象可知:抛物线与直线y=2有两个交点,
故关于x的方程ax2+bx+c=2有两个不相等实数根,故③正确;
由图象可知:当x>−2时,y随x增大而减小,故④错误;
∵图象开口向下,
∴a<0
∵b=4a,
∴b<0
结合抛物线与x轴的两个交点范围可知,抛物线与y轴负半轴相交,
∴c<0,
∴abc<0,故⑤错误;
由图象可知:y的最大值为3,故⑥错误;
故选:B
8.(2023·广东茂名·统考二模)已知函数y=x2−2x+3在闭区间0,m上有最大值3,最小值2,则m的取值范围是( )
A.m≥1B.0≤m≤2C.1≤m≤2D.m≤2
【答案】C
【分析】本题考查了二次函数的性质,由二次函数的解析式可得出抛物线开口向上,对称轴为x=1,顶点坐标为1,2,与y轴的交点为0,3,可画出大致图象,由函数y=x2−2x+3在闭区间0,m上有最大值3,最小值2,结合图象即可得出答案,熟练掌握二次函数的性质,采用数形结合的思想是解此题的关键.
【详解】解:∵二次函数y=x2−2x+3=x−12+2,
∴抛物线开口向上,对称轴为x=1,顶点坐标为1,2,
当x=0时,y=3,
∴与y轴的交点为0,3,
其大致图象如图所示:
,
由对称性可知,当y=3时,x=0或x=2,
∵二次函数y=x2−2x+3在闭区间0,m上有最大值3,最小值2,
∴1≤m≤2,
故选:C.
9.(2023·四川广安·统考一模)如图是二次函数y=ax2+bx+ca≠0的图象,已知关于x的方程ax2+bx+c=0的一个根为x1=7,则另一个根x2为 .
【答案】−1
【分析】本题主要考查二次函数的图象与性质,根据二次函数图象的对称性求出点7,0关于对称轴轴x=1的对称点−1,0即可.
【详解】解:根据图象知,抛物线y=ax2+bx+ca≠0的对称轴为直线x=1,且与x轴的一个交点为7,0,则另一个交点为−1,0,
所以,关于x的方程ax2+bx+c=0的另一个根为−1,
故答案为:−1.
10.(2023·四川广安·统考一模)已知二次函数y=x2−2tx+3的图象上两点Am,ℎ,Bn,ℎ,且满足−8≤m+n≤−6.当−4≤x≤−2时,该函数的最大值为2t+12,则t的值为 .
【答案】−134
【分析】本题考查了二次函数图象上点的坐标特征,二次函数的最值,根据二次函数的对称性以及对称轴方程得到−−2t2×1=m+n2,即t=m+n2,由−8≤m+n≤−6得到−4≤t≤−3,根据题意x=−2时,函数有最大值4+4t+3,则4+4t+3=2t+12,解方程即可.
【详解】解:∵二次函数y=x2−2tx+3的图象上两点Am,ℎ,Bn,ℎ,
∴−−2t2×1=m+n2,
∴t=m+n2,
∵−8≤m+n≤−6,
∴−4≤t≤−3,
∵当−4≤x≤−2时,该函数的最大值为2t+12,
∴x=−2时,函数有最大值4+4t+3=2t+12,
解得t=−134.
故答案为:−134.
11.(2023·广东佛山·佛山市南海区里水镇里水初级中学校考三模)如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是2,4,3,0,过点A的反比例函数y=kx的图象交BC于D.
(1)点B的坐标为______.
(2)点D是BC的中点吗?请说明理由;
(3)连接AD,求四边形AOCD的面积.
【答案】(1)5,4
(2)理由见解析
(3)四边形AOCD的面积为9
【分析】本题考查反比例函数系数k的几何意义,平行四边形的性质,反比例函数的解析式,一次函数的解析式.
(1)根据平行四边形的性质即可求出B点坐标;
(2)由点A的坐标进可得出反比例函数的解析式,利用待定系数法求出直线BC的解析式,即可求出D点坐标,即可得出结论;
(3)由(2)知点D为BC的中点,△ABD的面积=14平行四边形AOCB的面积,即可求出四边形AOCD的面积..
【详解】(1)解:∵四边形ABCD是平行四边形,A、C的坐标分别是2,4,3,0,
∴OC=AB=3,
∴点B的坐标为:5,4;
(2)解:把点A2,4代入反比例函数y=kx得:k=8,
∴反比例函数的解析式为:y=8x;
设直线BC的解析式为:y=kx+bk≠0,
把点B5,4,C3,0代入得:
5k+b=43k+b=0,
解得:k=2b=−6,
∴直线BC的解析式为:y=2x−6,
解方程组
y=2x−6y=8x 得:x=4y=2或 x=−1y=−8(不合题意,舍去),
∴点D的坐标为:4,2,
即点D为BC的中点;
(3)解:如图,连接AD,
∵点D为BC的中点,
∴ △ABD的面积=14平行四边形AOCB的面积,
∴四边形AOCD的面积=平行四边形AOCB的面积−△ABD的面积=3×4−14×3×4=9;
∴四边形AOCD的面积为9.
12.(2023·吉林松原·校联考三模)如图,在平面直角坐标系中,二次函数y=−x2+bx+c的图象经过点A0,3,点B−1,1.
(1)求此二次函数的解析式;
(2)当−3≤x≤3时,求二次函数y=−x2+bx+c的最大值和最小值;
(3)点P为此函数图象上任意一点,其横坐标为m,过点P作PQ∥x轴,点Q的横坐标为−3m−2.已知点P与点Q不重合,且线段PQ的长度随m的增大而增大.
①求m的取值范围;
②当PQ<14时,直接写出线段PQ与二次函数y=−x2+bx+c−12≤x<3的图象交点个数及对应的m的取值范围.
【答案】(1)y=−x2+x+3;
(2)最大值:134,最小值:−9;
(3)−12
(2)把抛物线化为顶点式,再结合函数的性质可得最大值与最小值,即可得到范围;
(3)①根据PQ∥x轴,确定P、Q的纵坐标相同,先表示线段PQ的长度,再根据函数的性质列不等式求解即可.②根据0
c=3−1−b+c=1,
解得:b=1c=3,
∴二次函数的解析式为:y=−x2+x+3;
(2)y=−x2+x+3=−x−122+134,
∴抛物线开口向下,对称轴为直线 x=12,
∴当x=12时,y最大值=134;
∵12−−3=312>3−12=212,
∴当x=−3时,y最小值=−32−3+3=−9;
(3)①PQ=−3m−2−m=−4m−2,
当−4m−2>0时,PQ=−4m−2的长度随m的增大而减小,
当−4m−2<0时,PQ=4m+2,PQ的长度随m增大而增大.
∴−4m−2<0满足题意,
解得:m>−12;
②∵0
解得:−12
如图,当−12
此时抛物线与线段PQ有1个交点,
∵抛物线上横坐标为−12的点关于直线x=12的对称点的横坐标为32,
当12
如图,
此时抛物线与线段PQ有两个交点,
当32
如图,
此时抛物线与线段PQ有1个交点,
综上所述, −12
考点要求
命题预测
平面直角坐标系与函数
该专题内容是初中代数最重要的部分,是代数的基础,非常重要,年年都会考查,分值为10分左右.预计2024年各地中考还将出现,在选择、填空题中出现的可能性较大.
一次函数、反比例函数、二次函数的性质
一次函数在中考数学中主要考察其图象、性质以及其简单应用,其中,图象的性质经常以选择、填空题形式出现,而简单应用题型的考察较为灵活,单独考察一次函数的题目占比并不是很多,更多的是考察一次函数与其他几何知识的结合.
反比例函数在中考数学中主要考察其图象与性质,常和一次函数的图象结合考察,题型以选择题为主;另外,在填空题中,对反比例函数点的坐标特征考察的比较多,而且难度逐增大,考题常结合其他规则几何图形的性质一起出题,多数题目的技巧性较强,复习中需要多加注意.另外解答题中还会考察反比例函数的解析式的确定,也是常和一次函数结合,顺带也会考察其与不等式的关系.
在中考中,二次函数的出题形式不固定,题目的难度都在中上等,也常作为中考中难度较大的一类压轴题的问题背景,占的分值也较高.而考察的内容主要有:二次函数图象与性质、解析式的求法、几何变化、以及函数与几何图形相关的综合应用等.
点P(x,y)的位置
在象限内
第一象限
x>0,y>0
第二象限
x<0,y>0
第三象限
x<0,y<0
第四象限
x>0,y<0
坐标轴上
x轴
y=0
y轴
x=0
原点
x=y=0
在角平分线上
第一、三象限
x=y
第二、四象限
x= -y
在平行坐标轴的直线上
平行x轴
所有点的 纵 坐标相等
平行y轴
所有点的 横 坐标相等
变换方式
具体变换过程
变换后的坐标
点P(x,y)
平移变换
向左平移a个单位
(x-a,y)
向右平移a个单位
(x+a,y)
向上平移a个单位
(x,y+a)
向下平移a个单位
(x,y-a)
简单记为“点的平移右加左减,上加下减”
点P(x,y)
具体变换过程
变换后的坐标
旋转变换
绕原点顺时针旋转90°
(y,-x)
绕原点顺时针旋转180°
(-x,-y)
绕原点逆时针旋转90°
(-y,x)
绕原点逆时针旋转180°
(-x,-y)
点P(x,y)
具体变换过程
变换后的坐标
对称变换
关于x轴对称
(x,-y)
关于y轴对称
(-x,y)
关于原点对称
(-x,-y)
简单记为“关于谁对称谁不变,关于原点对称都改变”
关于x=m对称
(2m-x,y)
关于y=n对称
(x,2n-y)
xkg
……
0.25
0.5
1
2
4
……
ycm
……
……
xkg
……
0.25
0.5
1
2
4
……
ycm
……
4
2
1
12
14
……
RΩ
…
1
a
3
4
6
…
IA
…
4
3
2.4
2
b
…
x/cm
0
0.5
1
1.5
1.8
2
2.5
3
3.5
4
4.5
5
y/cm
4
3.96
3.79
3.47
a
2.99
2.40
1.79
1.23
0.74
0.33
0
x
……
﹣5
﹣4
﹣3
﹣2
﹣1
1
2
3
4
5
……
y
……
﹣3.8
﹣2.5
﹣1
1
5
5
a
﹣1
﹣2.5
﹣3.8
……
点P(x,y)的位置
在象限内
第一象限
x>0,y>0
第二象限
x<0,y>0
第三象限
x<0,y<0
第四象限
x>0,y<0
坐标轴上
x轴
y=0
y轴
x=0
原点
x=y=0
在角平分线上
第一、三象限
x=y
第二、四象限
x= -y
在平行坐标轴的直线上
平行x轴
所有点的 纵 坐标相等
平行y轴
所有点的 横 坐标相等
变换方式
具体变换过程
变换后的坐标
点P(x,y)
平移变换
向左平移a个单位
(x-a,y)
向右平移a个单位
(x+a,y)
向上平移a个单位
(x,y+a)
向下平移a个单位
(x,y-a)
简单记为“点的平移右加左减,上加下减”
对称变换
关于x轴对称
(x,-y)
关于y轴对称
(-x,y)
关于原点对称
(-x,-y)
简单记为“关于谁对称谁不变,关于原点对称都改变”
关于x=m对称
(2m-x,y)
关于y=n对称
(x,2n-y)
旋转变换
绕原点顺时针旋转90°
(y,-x)
绕原点顺时针旋转180°
(-x,-y)
绕原点逆时针旋转90°
(-y,x)
绕原点逆时针旋转180°
(-x,-y)
优点
缺点
解析法
准确反映整个变化过程中自变量与函数的关系
求对应值是要经过比较复杂的计算,而且实
际问题中有的函数值不一定能用解析式表示
列表法
自变量和与它对应的函数值数据一目了然
所列对应数值个数有限,不容易看出自变量
与函数值的对应关系,有局限性
图像法
形象的把自变量和函数值的关系表示出来
图像中只能得到近似的数量关系
x
12
1
2
3
4
5
6
7
8
y
m
0
−1
−23
0
45
n
187
72
图象特征
正比例函数y=kx(k为常数,k≠0)必过点(0,0)、(1,k).
一次函数y=kx+b(k,b是常数,k≠0)必过点(0,b)、(- bk,0)
增减性
k>0
k<0
从左向右看图像呈上升趋势,
y随x的增大而增大
从左向右看图像呈下降趋势,
y随x的增大而减少
图象
b>0
b=0
b<0
b>0
b=0
b<0
经过象限
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
与y轴
交点位置
b>0,交点在y轴正半轴上;b=0,交点在原点;b<0,交点在y轴负半轴上
一次函数图象与正比例函数图象的关系
一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到:
当b>0时,向上平移b个单位长度;
当b<0时,向下平移|b|个单位长度
平移口诀:左加有减,上加下减
一次函数图象确定方法
因为一次函数的图象是一条直线,由两点确定一条直线可知画一次函数图象时,只要取两点即可,
1)画一次函数的图象,只需过图象上两点作直线即可,一般取(0,b),(−bk,0)两点;
2)画正比例函数的图象,只要取一个不同于原点的点即可.
图象特征
1)反比例函数的图象是双曲线,它有两个分支,它的图象与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴.
2)反比例函数的图象既是轴对称图形,又是中心对称图形,其对称轴为直线y=±x,对称中心为原点.
性质
表达
式
y=kx(k为常数,k≠0)
图象
k>0
k<0
经过
象限
一、三象限(x、y同号)
二、四象限(x、y异号)
增减性
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
对称性
①图象关于原点对称,即若(a,b)在双曲线的一支上,则(-a,-b)在双曲线的另一支上;
②图象关于直线y=x 对称,即若(a,b)在双曲线的一支上,则(b,a)在双曲线的另一支上;
③图象关于直线y=−x对称,即若(a,b)在双曲线的一支上,则(-b,-a)在双曲线的另一支上.
即:反比例函数的图象关于直线y=±x成轴对称,关于原点成中心对称.
x
1
2
4
y
4
2
1
图象特征
二次函数的图象是一条关于某条直线对称的曲线,这条曲线叫抛物线,该直线叫做抛物线的对称轴,对称轴与抛物线的交点叫做抛物线的顶点.
基本形式
y=ax2
y=ax2+k
y=a(x-h)2
y=a(x-h)2+k
y=ax2+bx+c
图象
a>0
a<0
对称轴
y轴
y轴
x=h
x=h
x=−b2a
顶点坐标
(0,0)
(0,k)
(h,0)
(h,k)
(−b2a,4ac−b24a)
最值
a>0
开口向上,顶点是最低点,此时 y 有最小值;
a<0
开口向下,顶点是最高点,此时y有最大值.
【小结】二次函数最小值(或最大值)为0(k或4ac−b24a).
增
减
性
a>0
在对称轴的左边y随x的增大而减小,在对称轴的右边y随x的增大而增大.
a<0
在对称轴的左边y随x的增大而增大,在对称轴的右边y随x的增大而减小.
符号
图象特征
备注
a
a>0
开口向上
a的正负决定开口方向,a的大小决定开口的大小(|a|越大,抛物线的开口小).
a<0
开口向下
b
b=0
坐标轴是y轴
ab>0(a,b同号)
对称轴在y轴左侧
左同右异
ab<0((a,b异号))
对称轴在y轴右侧
c
c=0
图象过原点
c决定了抛物线与y轴交点的位置.
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
自变量x的值
函数值
图象上对应点的位置
结论
-2
4a-2b+c
x轴的上方
4a-2b+c >0
x轴上
4a-2b+c =0
x轴的下方
4a-2b+c <0
-1
a-b+c
x轴的上方
a-b+c >0
x轴上
a-b+c =0
x轴的下方
a-b+c <0
1
a+b+c
x轴的上方
a+b+c >0
x轴上
a+b+c =0
x轴的下方
a+b+c <0
2
4a+2b+c
x轴的上方
4a+2b+c >0
x轴上
4a+2b+c =0
x轴的下方
4a+2b+c <0
自变量取值范围
图象
最大值
最小值
全体实数
a>0
当x=−b2a时,二次函数取得最小值4ac−b24a
a<0
当x=−b2a时,二次函数取得最大值4ac−b24a
x1≤x≤x2
a>0
当x=x2时,二次函数取得最大值y2
当x=−b2a时,二次函数取得最小值4ac−b24a
当x=x1时,二次函数取得最大值y1
当x=−b2a时,二次函数取得最小值4ac−b24a
当x=x2时,二次函数取得最大值y2
当x=x1时,二次函数取得最小值y1
平移方式(n>0)
一般式y=ax2+bx+c
顶点式y=a(x–h) 2+k
平移口诀
向左平移n个单位
y=a(x+n)2+b(x+n)+c
y=a(x-h+n) 2+k
左加
向右平移n个单位
y=a(x-n)2+b(x-n)+c
y=a(x-h-n)2+k
右减
向上平移n个单位
y=ax2+bx+c+n
y=a(x-h)2+k+n
上加
向下平移n个单位
y=ax2+bx+c-n
y=a(x-h)2+k-n
下减
正比例函数
一次函数
区别
一般形式
y=kx+b(k是常数,且k≠0)
y=kx+b(k,b是常数,且k≠0)
图象
经过原点的一条直线
一条直线
k,b符号
的作用
k的符号决定其增减性,
同时决定直线所经过的象限
k的符号决定其增减性;
b的符号决定直线与y轴的交点位置;
k,b的符号共同决定直线在直角坐标系的位置
求解析式
的条件
只需要一对x,y的对应值
或一个点的坐标
需要两对x,y的对应值或两个点的坐标
联系
1)正比例函数是特殊的一次函数.
2)正比例函数图象与一次函数图象的画法一样,都是过两点画直线,但画一次函数的图象需取两个不同的点,而画正比例函数的图象只要取一个不同于原点的点即可.
3)一次函数y=kx+b(k≠0)的图象可以看作是正比例函数y=kx(k≠0)的图象沿y轴向上(b>0)或向下(b<0)平移|b|个单位长度得到的.由此可知直线y=kx+b(k≠0,b≠0)与直线y=kx(k≠0)平行.
4)一次函数与正比例函数有着共同的性质:
①当k>0时,y的值随x值的增大而增大;
②当k<0时,y的值随x值的增大而减小.
平移方式(n>0)
一般式y=ax2+bx+c
顶点式y=a(x–h) 2+k
平移口诀
向左平移n个单位
y=a(x+n)2+b(x+n)+c
y=a(x-h+n) 2+k
左加
向右平移n个单位
y=a(x-n)2+b(x-n)+c
y=a(x-h-n)2+k
右减
向上平移n个单位
y=ax2+bx+c+n
y=a(x-h)2+k+n
上加
向下平移n个单位
y=ax2+bx+c-n
y=a(x-h)2+k-n
下减
变换前
变换方式
变换后
口诀
y=a(x-h)²+k
绕顶点旋转180°
y= -a(x-h)²+k
a变号,h、k均不变
绕原点旋转180°
y= -a(x+h)²-k
a、h、k均变号
沿x轴翻折
y= -a(x-h)²-k
a、k变号,h不变
沿y轴翻折
y= a(x+h)²+k
a、h不变,h变号
专题02 函数及其性质(15题型3类型+限时检测)-2024年中考数学二轮复习讲义(全国通用): 这是一份专题02 函数及其性质(15题型3类型+限时检测)-2024年中考数学二轮复习讲义(全国通用),文件包含专题02函数及其性质原卷版docx、专题02函数及其性质解析版docx等2份试卷配套教学资源,其中试卷共136页, 欢迎下载使用。
专题13 二次函数性质压轴(10题型)(讲练)-中考数学二轮复习讲练测(全国通用): 这是一份专题13 二次函数性质压轴(10题型)(讲练)-中考数学二轮复习讲练测(全国通用),文件包含专题13二次函数性质压轴讲练原卷版docx、专题13二次函数性质压轴讲练解析版docx等2份试卷配套教学资源,其中试卷共92页, 欢迎下载使用。
专题02 函数及其性质(24题型)(讲练)-中考数学二轮复习讲练测(全国通用): 这是一份专题02 函数及其性质(24题型)(讲练)-中考数学二轮复习讲练测(全国通用),文件包含专题02函数及其性质讲练原卷版docx、专题02函数及其性质讲练解析版docx等2份试卷配套教学资源,其中试卷共180页, 欢迎下载使用。












