





专题14 二次函数与几何压轴(课件)-2024年中考数学二轮复习课件(全国通用)
展开第二轮复习是为了将第一轮复习的知识点、线结合,交织成知识网络,是第一轮复习的延伸和提高,所以要注重与实际问题的联系,以实现数学能力的培养和提高。本轮复习应该侧重培养数学能力,在第一轮复习的基础上,适当增加难度,要有针对性,围绕热点、难点、创新点、重点,特别是近几年的中考常考内容选定专题。一、复习方法:1.以专题复习为主。2.重视方法思维的训练。3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。二、复习难点:1.专题的选择要准,安排时间要合理。2.专项复习要以题带知识。3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
专题14 二次函数与几何压轴
2024年中考数学二轮复习课件
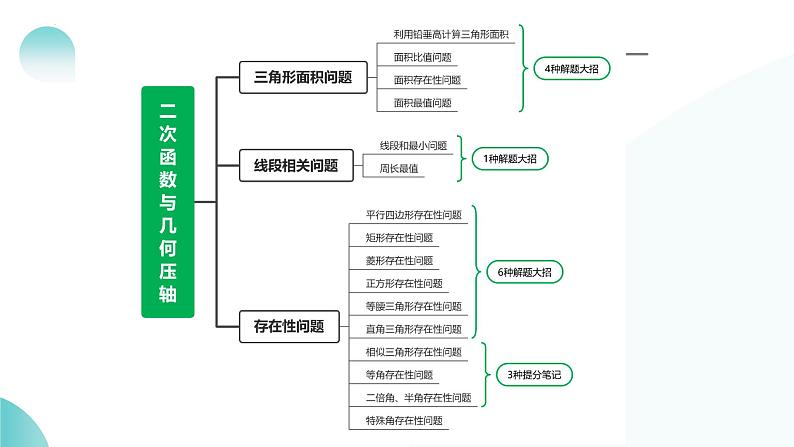
类型一 利用铅垂高计算三角形面积
对于阿氏圆而言:当系数k<1的时候,一般情况下,考虑向内构造.当系数k>1的时候,一般情况下,考虑向外构造.【注意事项】针对求PA+kPB的最小值问题时,当轨迹为直线时,运用“胡不归模型”求解;当轨迹为圆形时,运用“阿氏圆模型”求解.
思路 1:从判定出发1)若已知菱形,则加有一个角为直角或对角线相等:2)若已知矩形,则加有一组邻边相等或对角线互相垂直:3)若已知对角线互相垂直或平分或相等,则加上其他条件.思路 2:构造三乖直全等若条件并未给关于四边形及对角线的特殊性,则考虑在构成正方形的4个顶点中任取3个,必是等腰直角三角形,若已知两定点,则可通过构造三垂直全等来求得第3个点,再求第4点.总结:构造三垂直全等的思路仅适合已知两定点的情形,若题目给了4个动点,则考虑矩形的判定出发,观察该四边形是否己为某特殊四边形,考证还需满足的其他关系.(正方形的存在性问题在中考中出现得并不多,正方形多以小题压轴为主)
问题总结:1) 两定一动:动点可在直线上、抛物线上;2)一定两动:两动点必有关联,可表示线段长度列方程求解;3)三动点:分析可能存在的特殊边、角,以此为突破口.
【相似判定】判定1:三边对应成比例的两个三角形是相似三角形;判定2:两边对应成比例且夹角相等的两个三角形是相似三角形;判定3:有两组角对应相等的三角形是相似三角形.【思路总结】根据相似三角形的做题经验,可以发现,判定1基本是不会用的,这里也一样不怎么用,对比判定2、3可以发现,都有角相等.所以,要证相似的两个三角形必然有相等角,关键点也是先找到一组相等角.然后再找:1)两相等角的两边对应成比例;2)还存在另一组角相等.事实上,坐标系中在已知点的情况下,线段长度比角的大小更容易表示,因此选择方法可优先考虑思路1.【解题方法】1)找对应等角2)分类讨论3)设点表示线段4)列方程求解5)检验
【常见的构角方法】1)平行线的同位角、内错角相等;2)等腰三角形的等边对等角;3)角平分线分的两个角相等;4)全等(相似)三角形对应角相等;5)若两角的三角函数值相等,则两角相等;6)同圆或等圆中,同弧或等弧所对的圆周角相等.角度转化的一般方法为:通过锐角三角形函数、特殊角的三角函数值,相似三角形或等腰三角形的性质,转化为常见的类型,然后利用解直角三角形、相似三角形边的比例关系作为计算工具去计算求解,难度相对较大.
探究角度问题的一般步骤如下:1)读题、理解题意,画图;2)分析动点、定点、找不变特征(如角有两边,其中一条边是确定的);3)确定分类特征,进行分类讨论;4)将角度进行转化.
【构造二倍角的方法】方法一:构造二倍角的三角函数,并通过勾股定理求解.(左图)方法二:等腰三角形的外角.(右图)把2倍角转化为角相等的常用方法1) 利用角平分线转化;2) 利用等腰三角形顶角的外角转化;3) 利用直角三角形斜边中线得等腰三角形转化.
专题13 二次函数性质压轴(课件)-2024年中考数学二轮复习课件(全国通用): 这是一份专题13 二次函数性质压轴(课件)-2024年中考数学二轮复习课件(全国通用),共53页。PPT课件主要包含了考情分析,知识建构,考点精讲等内容,欢迎下载使用。
专题12 圆压轴(课件)-2024年中考数学二轮复习课件(全国通用): 这是一份专题12 圆压轴(课件)-2024年中考数学二轮复习课件(全国通用),共45页。PPT课件主要包含了专题12圆压轴,考情分析,考点精讲等内容,欢迎下载使用。
专题11 四边形压轴(课件)-2024年中考数学二轮复习课件(全国通用): 这是一份专题11 四边形压轴(课件)-2024年中考数学二轮复习课件(全国通用),共42页。PPT课件主要包含了专题11四边形压轴,考情分析,考点精讲等内容,欢迎下载使用。












