中考数学一轮总复习： 矩形、菱形、正方形 课件

这是一份中考数学一轮总复习： 矩形、菱形、正方形 课件，共32页。PPT课件主要包含了矩形常考点，菱形常考点，正方形常考点，中点四边形，°或80°等内容，欢迎下载使用。
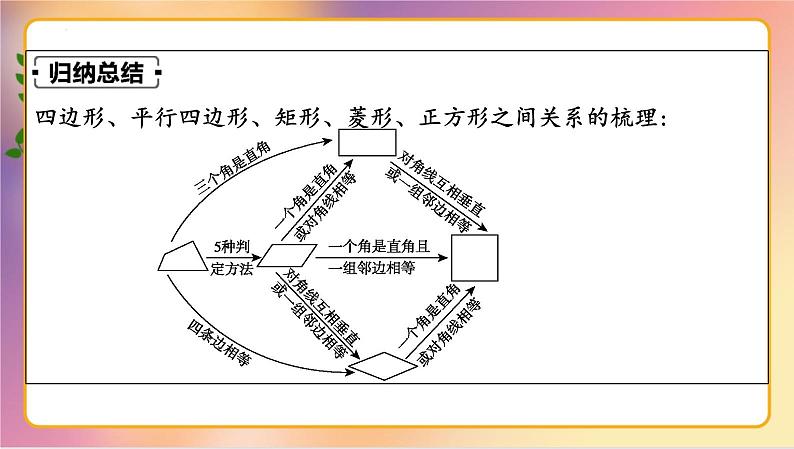
四边形、平行四边形、矩形、菱形、正方形之间关系的梳理:
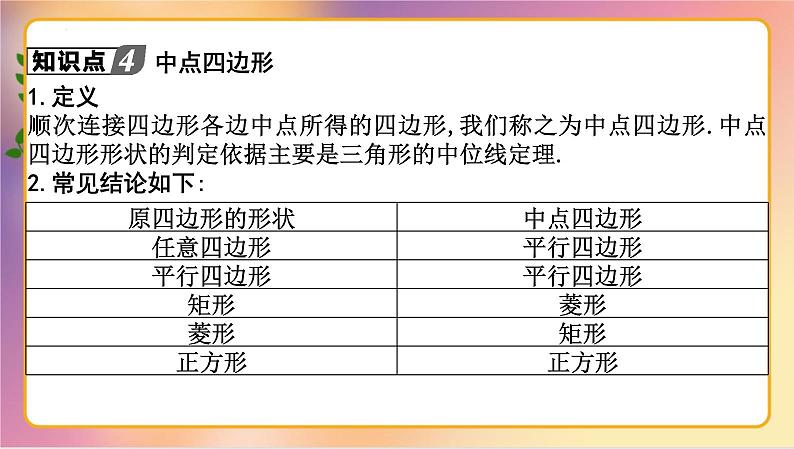
1.定义顺次连接四边形各边中点所得的四边形,我们称之为中点四边形.中点四边形形状的判定依据主要是三角形的中位线定理.2.常见结论如下:
3.中点四边形的相关知识(1)无论原四边形的形状如何改变,中点四边形的形状始终是平行四边形;(2)中点四边形的周长是原四边形两条对角线的长度之和;(3)中点四边形的面积是原四边形面积的一半.
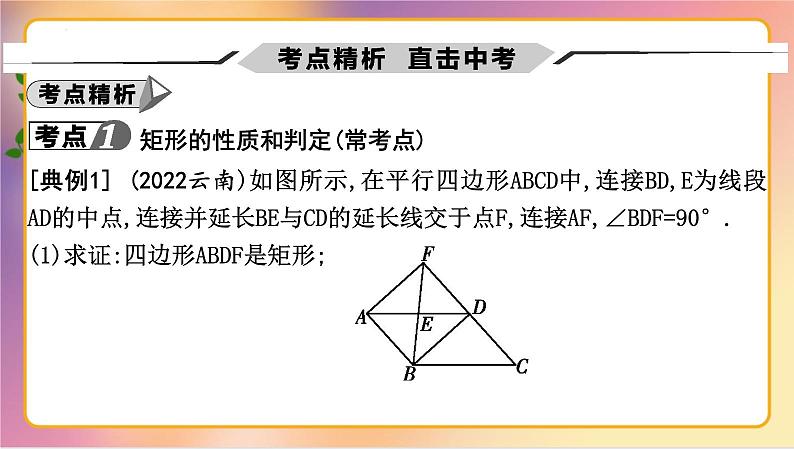
矩形的性质和判定(常考点)
[典例1] (2022云南)如图所示,在平行四边形ABCD中,连接BD,E为线段AD的中点,连接并延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,求四边形ABCF的面积S.
判定矩形的思路(1)利用直角判定矩形的思路①任意四边形+三个直角⇒矩形;②平行四边形+一个直角⇒矩形.(2)利用对角线判定矩形的思路平行四边形+对角线相等⇒矩形.
[变式1] (2023台州)如图所示,在矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为F,则BF的长为　 　. 
[变式2] (2023内江)如图所示,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.(1)求证:FA=BD;
证明:(1)∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE.∵E为AD的中点,∴AE=DE,∴△AEF≌△DEC(AAS),∴AF=DC.∵D为BC的中点,∴BD=CD,∴AF=BD.
(2)连接BF,若AB=AC,求证:四边形ADBF是矩形.
证明:(2)∵AF=BD,AF∥BD,∴四边形ADBF是平行四边形.∵AB=AC,D为BC的中点,∴AD⊥BC,∴∠ADB=90°,∴平行四边形ADBF是矩形.
菱形的性质和判定(常考点)
[典例2] (2022聊城)如图所示,△ABC中,点D是AB上一点,点E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.(1)求证:AD=CF.
(1)由CF∥AB,得∠ADF=∠CFD,∠DAC=∠FCA,又AE=CE,可证△ADE≌△CFE(AAS),即得AD=CF;
(1)证明:∵CF∥AB,∴∠ASDF=∠CFD,∠DAC=∠FCA.∵点E是AC的中点,∴AE=CE,∴△ADE≌△CFE(AAS),∴AD=CF.
(2)连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形?证明你的结论.
判定菱形的思路(1)利用边判定菱形的思路①平行四边形+一组邻边相等⇒菱形;②四边形+四条边相等⇒菱形.(2)利用对角线判定菱形的思路平行四边形+对角线互相垂直⇒菱形.
[变式3] (2023绍兴)如图所示,在菱形ABCD中,∠DAB=40°,连接AC,以点A为圆心,AC长为半径作弧,交直线AD于点E,连接CE,则∠AEC的度数是　 　. 
[变式4] (2022滨州)如图所示,菱形ABCD的边长为10,∠ABC=60°,对角线AC,BD相交于点O,点E在对角线BD上,连接AE,作∠AEF=120°,且边EF与直线DC相交于点F.(1)求菱形ABCD的面积;
(2)求证:AE=EF.
(2)证明:连接EC,如图所示.∵四边形ABCD是菱形,∠ABC=60°,∴EO垂直平分AC,∠BCD=120°,∴EA=EC,∠DCA=60°,∴∠EAC=∠ECA,∠ACF=120°.∵∠AEF=120°,∴∠EAC+∠EFC=360°-∠AEF-∠ACF=360°-120°-120°=120°.∵∠ECA+∠ECF=120°,∴∠EFC=∠ECF,∴EC=EF,∴AE=EF.
正方形的性质和判定(常考点)
[典例3] (2022无锡)如图所示,正方形ABCD的边长为8,点E是CD的中点, HG垂直平分AE且分别交AE,BC于点H,G,则BG=　 　. 
连接AG,EG,根据线段垂直平分线性质可得AG=EG,由点E是CD的中点,得CE=4,设BG=x,则CG=8-x,由勾股定理,可得出(8-x)2+ 42=82+x2,求解即可.
正方形的边、角、对角线性质(1)边:四条边都相等且每组对边平行;(2)角:四个角都是直角;(3)对角线:两条对角线相等且互相垂直平分,把正方形分成四个全等的等腰直角三角形.
[变式5] (2023宁夏)如图所示,在边长为2的正方形ABCD中,点E在AD上,连接EB,EC.则图中阴影部分的面积是　 　. 
[变式6] (2022恩施)如图所示,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
1.(2023上海)在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是(　　)A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D
2.(2022重庆B卷)如图所示,在正方形ABCD中,对角线AC,BD相交于点O,E,F分别为AC,BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为(　　)A.50°B.55°C.65°D.70°
4.(2023河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为　 　. 
5.(2022泰州)如图所示,线段DE与AF分别为△ABC的中位线与中线.(1)求证:AF与DE互相平分.
(1)证明:∵线段DE与AF分别为△ABC的中位线与中线,∴D,E,F分别是AB,AC,BC的中点,∴线段DF与EF也为△ABC的中位线,∴DF∥AC,EF∥AB,∴四边形ADFE是平行四边形,∴AF与DE互相平分.
(2)当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明 理由.