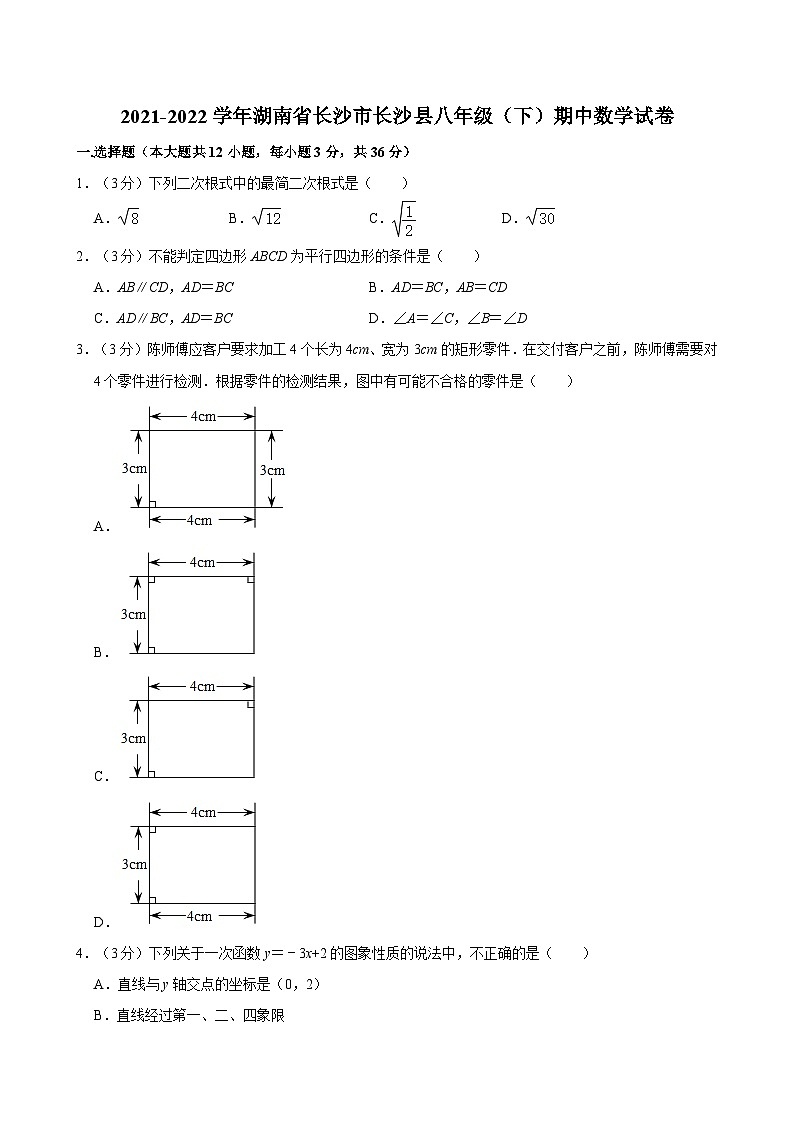
2021-2022学年湖南省长沙市长沙县八年级（下）期中数学试卷

这是一份2021-2022学年湖南省长沙市长沙县八年级（下）期中数学试卷，共25页。
A．B．C．D．
2．（3分）不能判定四边形ABCD为平行四边形的条件是（ ）
A．AB∥CD，AD＝BCB．AD＝BC，AB＝CD
C．AD∥BC，AD＝BCD．∠A＝∠C，∠B＝∠D
3．（3分）陈师傅应客户要求加工4个长为4cm、宽为3cm的矩形零件．在交付客户之前，陈师傅需要对4个零件进行检测．根据零件的检测结果，图中有可能不合格的零件是（ ）
A．
B．
C．
D．
4．（3分）下列关于一次函数y＝﹣3x+2的图象性质的说法中，不正确的是（ ）
A．直线与y轴交点的坐标是（0，2）
B．直线经过第一、二、四象限
C．y随x的增大而减小
D．与坐标轴围成的三角形面积为2
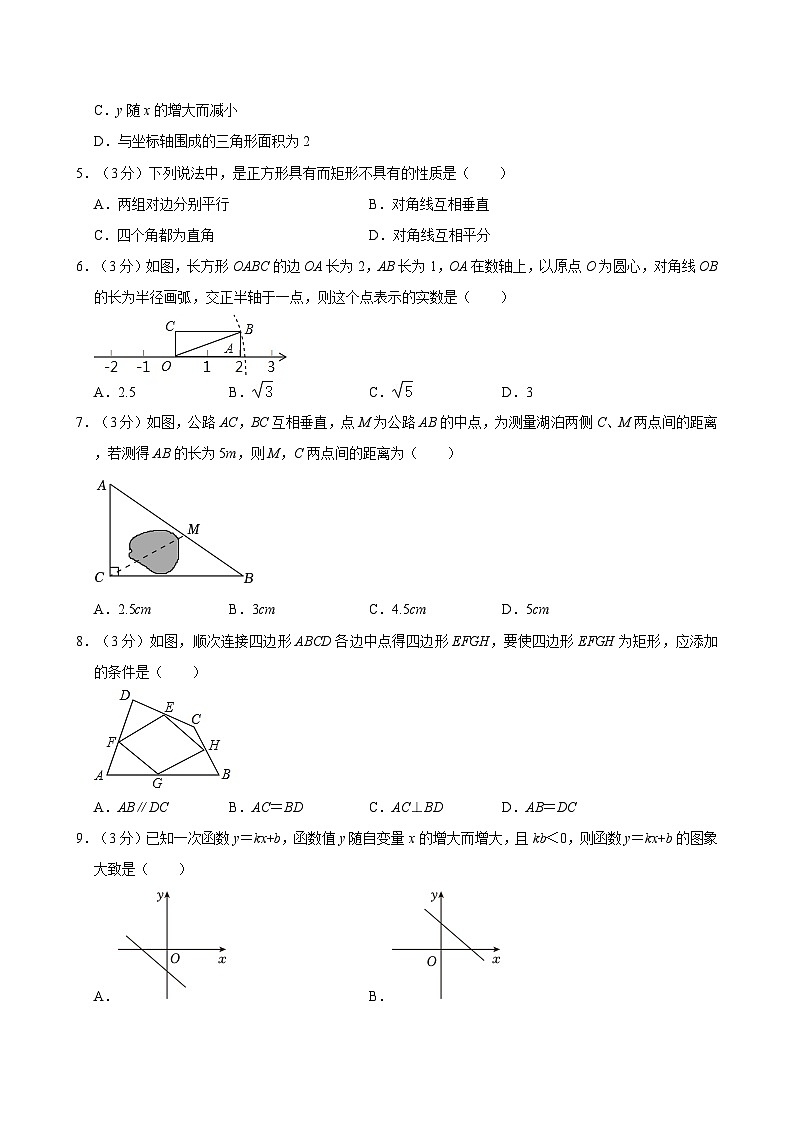
5．（3分）下列说法中，是正方形具有而矩形不具有的性质是（ ）
A．两组对边分别平行B．对角线互相垂直
C．四个角都为直角D．对角线互相平分
6．（3分）如图，长方形OABC的边OA长为2，AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（ ）
A．2.5B．C．D．3
7．（3分）如图，公路AC，BC互相垂直，点M为公路AB的中点，为测量湖泊两侧C、M两点间的距离，若测得AB的长为5m，则M，C两点间的距离为（ ）
A．2.5cmB．3cmC．4.5cmD．5cm
8．（3分）如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）
A．AB∥DCB．AC＝BDC．AC⊥BDD．AB＝DC
9．（3分）已知一次函数y＝kx+b，函数值y随自变量x的增大而增大，且kb＜0，则函数y＝kx+b的图象大致是（ ）
A．B．
C．D．
10．（3分）如图，菱形OABC的边OA在平面直角坐标系中的x轴上，∠AOC＝60°，OA＝4，则点C的坐标为（ ）
A．B．C．D．（2，2）
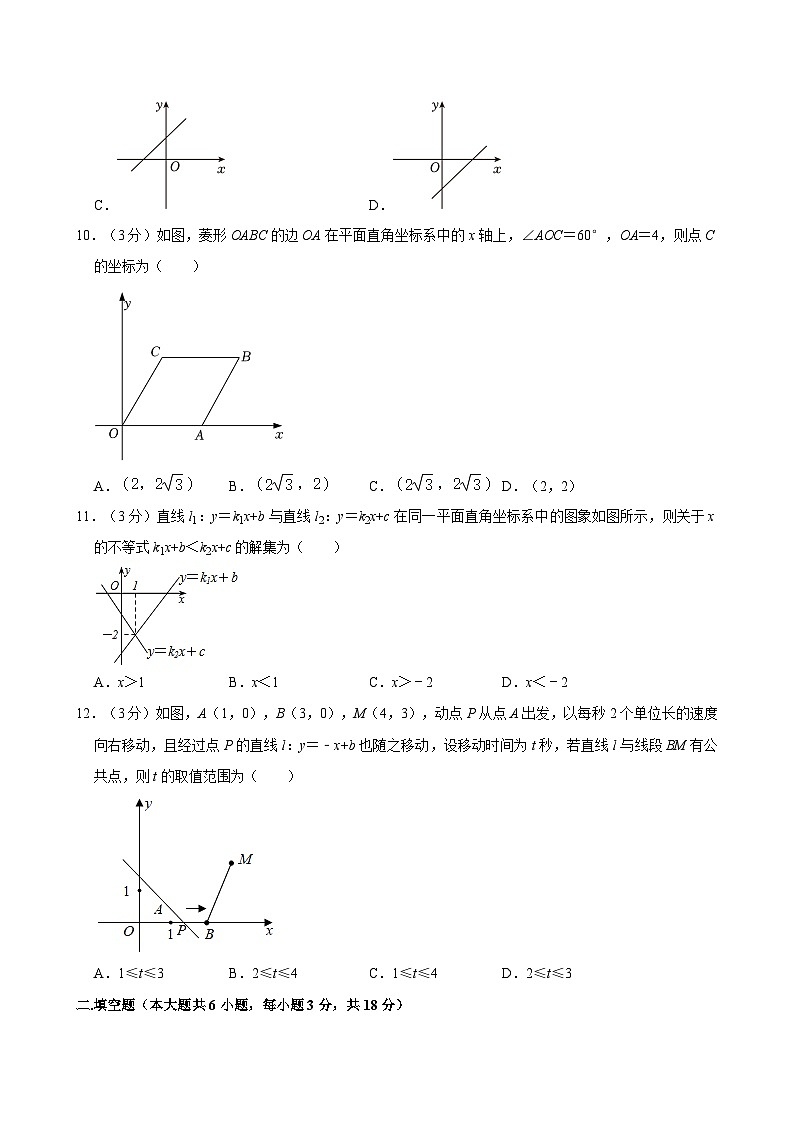
11．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x+c在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＜k2x+c的解集为（ ）
A．x＞1B．x＜1C．x＞﹣2D．x＜﹣2
12．（3分）如图，A（1，0），B（3，0），M（4，3），动点P从点A出发，以每秒2个单位长的速度向右移动，且经过点P的直线l：y＝﹣x+b也随之移动，设移动时间为t秒，若直线l与线段BM有公共点，则t的取值范围为（ ）
A．1≤t≤3B．2≤t≤4C．1≤t≤4D．2≤t≤3
二.填空题（本大题共6小题，每小题3分，共18分）
13．（3分）函数y＝的自变量x的取值范围是 ．
14．（3分）已知y与x成正比例，且x＝1时，y＝﹣2，则当x＝﹣1时，y＝ ．
15．（3分）点（x1，y1），（x2，y2）是一次函数y＝﹣2x+m上的点，如果x1＜x2，则y1 y2（填“＞”、“＝”、“＜”）．
16．（3分）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF＝6，则菱形ABCD的周长为 ．
17．（3分）如图，矩形OABC的顶点B的坐标为（4，3），则对角线AC的长等于 ．
18．（3分）我国古代九章算术中有数学发展史上著名的“葭生池中”问题：今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问：葭长几何？（1丈＝10尺）•意思是：有一个长方体池子，底面是边长为1丈的正方形，中间有芦苇，把高出水面1尺的芦苇拉向池边（芦苇没有折断），刚好贴在池边上，问：芦苇长多少尺？答：芦苇长 尺．
三.解答题（本大题共8小题，共66分。解答应写出文字说明、证明过程或演算步骤。）
19．（6分）计算：
（1）；
（2）．
20．（6分）如图，在Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，点D是Rt△ABC外一点，连接DC，DB，且CD＝2，．
（1）求BC的长；
（2）求证：△BCD是直角三角形．
21．（8分）一次函数y＝（2m+1）x+m﹣3．
（1）若函数图象经过原点，求m的值；
（2）若函数图象平行于直线y＝3x﹣3，求该函数解析式，并在所给的平面直角坐标系中画出函数的图象；
（3）在（1）的条件下，将正比例函数的图象向下平移4个单位，求出平移后的直线解析式．
22．（8分）如图，在▱ABCD中，F是BC的中点，连接AF并延长，交DC的延长线于点E，连接AC，BE．求证：四边形ABEC是平行四边形．
23．（9分）4月23日是“世界读书日”，甲书店在这一天举行了购书优惠活动．
甲书店：“与书相伴，遇见更好地为自己”，一次购书中标价总额不超过80元的按原价计费超过80元的部分5折．以x（单位：元）表示标价总额，y（单位：元）表示应支付金额．
（1）文文购买标价总额50元的书需付款 元；购买标价总额100元书需付款 元；
（2）求支付金额y关于x的函数解析式，并写出自变量的取值范围；
（3）当天，隔壁的乙书店：“阅读改变生活，共创文明长沙”活动：同样标价的书籍均按标价7折出售；若文文需买250元书，选择哪家书店去购书更省钱？说明你的理由．
24．（9分）如图，在四边形ABCD中，AB∥DC，AB＝DC，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E．
（1）求证：四边形ABCD是菱形；
（2）若，BD＝2，求CE的长．
25．（10分）如图，在平面直角坐标系中，函数y＝2x+8的图象分别交x轴、y轴于A、B两点，过点A的直线交y轴正半轴于点M，且点M为线段OB的中点．
（1）求直线AM的函数解析式．
（2）试在直线AM上找一点P，使得S△ABP＝S△AOB，请直接写出点P的坐标．
（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、B、M、H为顶点的四边形是平行四边形？若存在，请直接写出所有点H的坐标；若不存在，请说明理由．
26．（10分）在平面直角坐标系xOy中，对于任意两点M（x1，y1），N（x2，y2），定义如下：点M与点N的“直角距离”为|x1﹣x2|+|y1﹣y2|，记作dMN．
例如：点M（1，5）与N（7，2）的“直角距离”dMN＝|1﹣7|+|5﹣2|＝9．
（1）两点P1（﹣1，0）、P2（1，1）中，与原点O的“直角距离”等于1的点是 ；
（2）如图，已知点A（1，0），B（0，1），根据定义可知线段AB上的任意一点与原点O的“直角距离”都等于1．若点P（x，y）与原点O的“直角距离”dOP＝1，即|x﹣0|+|y﹣0|＝1．则当x＝时，点P的坐标为 ，请你在图中将所有满足条件的点P组成的图形补全；
（3）已知直线y＝kx+3和点C（2，0），若直线y＝kx+3上存在点D，满足dCD＝1，求k的取值范围．
2021-2022学年湖南省长沙市长沙县八年级（下）期中数学试卷
参考答案与试题解析
一.选择题（本大题共12小题，每小题3分，共36分）
1．（3分）下列二次根式中的最简二次根式是（ ）
A．B．C．D．
【分析】根据最简二次根式的概念：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式，结合选项求解即可．
【解答】解：A、＝2，故不是最简二次根式，本选项错误；
B、＝2，故不是最简二次根式，本选项错误；
C、＝，故不是最简二次根式，本选项错误；
D、是最简二次根式，本选项正确．
故选：D．
2．（3分）不能判定四边形ABCD为平行四边形的条件是（ ）
A．AB∥CD，AD＝BCB．AD＝BC，AB＝CD
C．AD∥BC，AD＝BCD．∠A＝∠C，∠B＝∠D
【分析】由平行四边形的判定方法对各个选项进行判断即可．
【解答】解：A、由AB∥CD，AD＝BC，不能判定四边形ABCD是平行四边形，故本选项符合题意；
B、∵AD＝BC，AB＝CD，
∴四边形ABCD是平行四边形，故本选项不符合题意；
C、∵AD∥BC，AD＝BC，
∴四边形ABCD是平行四边形，故本选项不符合题意；
D、∵∠A＝∠C，∠B＝∠D，
∴四边形ABCD是平行四边形，故本选项不符合题意；
故选：A．
3．（3分）陈师傅应客户要求加工4个长为4cm、宽为3cm的矩形零件．在交付客户之前，陈师傅需要对4个零件进行检测．根据零件的检测结果，图中有可能不合格的零件是（ ）
A．
B．
C．
D．
【分析】根据矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形；（2）有三个角是直角的四边形是矩形；（3）对角线互相平分且相等的四边形是矩形．
【解答】解：A、有一个角是直角的平行四边形是矩形，能判定矩形，不符合题意；
B、其中四边形中三个角都为直角，能判定矩形，不符合题意；
C、对角相等的四边形不一定是矩形，不能判定形状，符合题意；
D、一组对边平行且相等，能判定平行四边形，有一个角是直角的平行四边形是矩形，则能判定矩形，不符合题意．
故选：C．
4．（3分）下列关于一次函数y＝﹣3x+2的图象性质的说法中，不正确的是（ ）
A．直线与y轴交点的坐标是（0，2）
B．直线经过第一、二、四象限
C．y随x的增大而减小
D．与坐标轴围成的三角形面积为2
【分析】A、代入y＝0求出与之对应的x值，进而可得出直线与x轴的交点坐标；
B、由k＝﹣1＜0，b＝2＞0，利用一次函数图象与系数的关系可得出直线经过第一、二、四象限；
C、由k＝﹣1＜0，利用一次函数的性质可得出y随x的增大而减小；
D、代入x＝0求出与之对应的y值，进而可得出直线与y轴的交点坐标，再利用面积公式即可求出直线与坐标轴围成的三角形面积．
【解答】解：A、∵当x＝0时，﹣3x+2＝2，
∴直线与y轴交点的坐标是（0，2）；
B、∵k＝﹣3＜0，b＝2＞0，
∴直线经过第一、二、四象限；
C、∵k＝﹣1＜0，
∴y随x的增大而减小；
D、当x＝0时，y＝﹣1×0+2＝2，
∴直线与y轴交点的坐标为（0，2），
∴直线与坐标轴围成的三角形面积＝×2×＝．
故选：D．
5．（3分）下列说法中，是正方形具有而矩形不具有的性质是（ ）
A．两组对边分别平行B．对角线互相垂直
C．四个角都为直角D．对角线互相平分
【分析】根据正方形、矩形的性质即可判断．
【解答】解：因为正方形的对角相等，对角线相等、垂直、且互相平分，矩形的对角相等，对角线相等，互相平分，
所以正方形具有而矩形不具有的性质是对角线互相垂直．
故选：B．
6．（3分）如图，长方形OABC的边OA长为2，AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（ ）
A．2.5B．C．D．3
【分析】本题利用实数与数轴的关系及直角三角形三边的关系（勾股定理）解答即可．
【解答】解：由勾股定理可知，
∵OB＝＝，
∴这个点表示的实数是．
故选：C．
7．（3分）如图，公路AC，BC互相垂直，点M为公路AB的中点，为测量湖泊两侧C、M两点间的距离，若测得AB的长为5m，则M，C两点间的距离为（ ）
A．2.5cmB．3cmC．4.5cmD．5cm
【分析】根据直角三角形斜边上的中线性质得出CM＝AB，再求出答案即可．
【解答】解：∵公路AC，BC互相垂直，
∴∠ACB＝90°，
∵M为AB的中点，
∴CM＝AB，
∵AB＝5m，
∴CM＝2.5（m），
即M，C两点间的距离为2.5m，
故选：A．
8．（3分）如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）
A．AB∥DCB．AC＝BDC．AC⊥BDD．AB＝DC
【分析】根据矩形的判定定理（有一个角为直角的平行四边形是矩形）．先证四边形EFGH是平行四边形，要使四边形EFGH为矩形，需要∠EFG＝90度．由此推出AC⊥BD．
【解答】解：依题意得，四边形EFGH是由四边形ABCD各边中点连接而成，
连接AC、BD，故EF∥AC∥HG，EH∥BD∥FG，
所以四边形EFGH是平行四边形，
要使四边形EFGH为矩形，
根据矩形的判定（有一个角为直角的平行四边形是矩形）
故当AC⊥BD时，∠EFG＝∠EHG＝90度．四边形EFGH为矩形．
故选：C．
9．（3分）已知一次函数y＝kx+b，函数值y随自变量x的增大而增大，且kb＜0，则函数y＝kx+b的图象大致是（ ）
A．B．
C．D．
【分析】根据一次函数y＝kx+b的图象与k和b之间的关系即可解决问题．
【解答】解：因为一次函数y＝kx+b，函数值y随自变量x的增大而增大，
所以k＞0，
又因为kb＜0，
所以b＜0，
则一次函数y＝kx+b的图象与y轴交于负半轴．
所以D选项符合题意．
故选：D．
10．（3分）如图，菱形OABC的边OA在平面直角坐标系中的x轴上，∠AOC＝60°，OA＝4，则点C的坐标为（ ）
A．B．C．D．（2，2）
【分析】过C作CD⊥OA于D，由菱形的性质得OC＝OA＝4，再由含30°角的直角三角形的性质得OD＝OC＝2，然后由勾股定理得CD＝2，即可得出点C的坐标．
【解答】解：过C作CD⊥OA于D，如图：
则∠ODC＝90°，
∵四边形OABC是菱形，
∴OC＝OA＝4，
∵∠AOC＝60°，
∴∠OCD＝90°﹣∠AOC＝30°，
∴OD＝OC＝2，
∴CD＝＝＝2，
∴点C的坐标为（2，2），
故选：A．
11．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x+c在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＜k2x+c的解集为（ ）
A．x＞1B．x＜1C．x＞﹣2D．x＜﹣2
【分析】y＝k1x+b与直线l2：y＝k2x+c在同一平面直角坐标系中的交点是（1，﹣2），根据图象得到x＜1时不等式k1x+b＜k2x+c成立．
【解答】解：由图可得：l1与直线l2在同一平面直角坐标系中的交点是（1，﹣2），且x＜1时，直线l1的图象在直线l2的图象下方，故不等式k1x+b＜k2x+c的解集为：x＜1．
故选：B．
12．（3分）如图，A（1，0），B（3，0），M（4，3），动点P从点A出发，以每秒2个单位长的速度向右移动，且经过点P的直线l：y＝﹣x+b也随之移动，设移动时间为t秒，若直线l与线段BM有公共点，则t的取值范围为（ ）
A．1≤t≤3B．2≤t≤4C．1≤t≤4D．2≤t≤3
【分析】分别求出直线l经过点B、点M时的t值，即可得到t的取值范围．
【解答】解：当直线y＝﹣x+b过点B（3，0）时，
0＝﹣3+b，
解得：b＝3，
0＝﹣（1+2t）+3，
解得t＝1．
当直线y＝﹣x+b过点M（4，3）时，
3＝﹣4+b，
解得：b＝7，
0＝﹣（1+2t）+7，
解得t＝3．
故若l与线段BM有公共点，t的取值范围是：1≤t≤3，
故选：A．
二.填空题（本大题共6小题，每小题3分，共18分）
13．（3分）函数y＝的自变量x的取值范围是 x≥﹣1 ．
【分析】根据二次根式的被开方数是非负数列出不等式，解不等式得到答案．
【解答】解：由题意得：x+1≥0，
解得：x≥﹣1，
故答案为：x≥﹣1．
14．（3分）已知y与x成正比例，且x＝1时，y＝﹣2，则当x＝﹣1时，y＝ 2 ．
【分析】用待定系数法求正比例函数的解析式．
【解答】解：因为y与x成正比例，所以设正比例函数的解析式为y＝kx（k≠0），
把x＝1时，y＝﹣2代入得：k＝﹣2，
故此正比例函数的解析式为：y＝﹣2x，
当x＝﹣1时，y＝﹣2×（﹣1）＝2．
故答案为：2．
15．（3分）点（x1，y1），（x2，y2）是一次函数y＝﹣2x+m上的点，如果x1＜x2，则y1 ＞ y2（填“＞”、“＝”、“＜”）．
【分析】根据所给一次函数的性质即可解决问题．
【解答】解：因为一次函数解析式为y＝﹣2x+m，且﹣2＜0，
所以一次函数的函数值y随x的增大而减小．
又因为点（x1，y1），（x2，y2）是一次函数y＝﹣2x+m上的点，且x1＜x2，
所以y1＞y2．
故答案为：＞．
16．（3分）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF＝6，则菱形ABCD的周长为 48 ．
【分析】证明EF是△ABC的中位线，得BC＝2EF＝2×6＝12，再由菱形的性质得AB＝BC＝CD＝AD＝12，即可得出结论．
【解答】解：∵E、F分别是AB、AC的中点，
∴EF是△ABC的中位线，
∴BC＝2EF＝2×6＝12，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD＝12，
∴菱形ABCD的周长＝4×12＝48，
故答案为：48．
17．（3分）如图，矩形OABC的顶点B的坐标为（4，3），则对角线AC的长等于 5 ．
【分析】先求出OB的长，由矩形的性质可得AC＝BO＝5．
【解答】解：如图，连接OB，
∵点B的坐标为（4，3），
∴OB＝＝5，
∵四边形ABCO是矩形，
∴AC＝BO＝5，
故答案为：5．
18．（3分）我国古代九章算术中有数学发展史上著名的“葭生池中”问题：今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问：葭长几何？（1丈＝10尺）•意思是：有一个长方体池子，底面是边长为1丈的正方形，中间有芦苇，把高出水面1尺的芦苇拉向池边（芦苇没有折断），刚好贴在池边上，问：芦苇长多少尺？答：芦苇长 13 尺．
【分析】首先设芦苇长x尺，则为水深为（x﹣1）尺，根据勾股定理可得方程（x﹣1）2+52＝x2，进而得出答案．
【解答】解：设芦苇长x尺，由题意得：
（x﹣1）2+52＝x2，
解得：x＝13，
故答案为：13．
三.解答题（本大题共8小题，共66分。解答应写出文字说明、证明过程或演算步骤。）
19．（6分）计算：
（1）；
（2）．
【分析】（1）先根据二次根式的乘法法则运算，然后化简二次根式即可；
（2）先把各二次根式化为最简二次根式，然后合并同类二次根式即可．
【解答】解：（1）原式＝+
＝3+；
（2）原式＝3﹣2+
＝．
20．（6分）如图，在Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，点D是Rt△ABC外一点，连接DC，DB，且CD＝2，．
（1）求BC的长；
（2）求证：△BCD是直角三角形．
【分析】（1）在Rt△ABC中，根据勾股定理即可求得BC的长；
（2）利用勾股定理逆定理即可证明△BCD是直角三角形．
【解答】（1）解：∵Rt△ABC中，∠BCA＝90°，AC＝12，AB＝13，
∴BC＝＝＝5；
（2）证明：∵在△BCD中，CD＝4，BD＝3，BC＝5，
∴CD2+BD2＝42+32＝52＝BC2，
∴△BCD是直角三角形．
21．（8分）一次函数y＝（2m+1）x+m﹣3．
（1）若函数图象经过原点，求m的值；
（2）若函数图象平行于直线y＝3x﹣3，求该函数解析式，并在所给的平面直角坐标系中画出函数的图象；
（3）在（1）的条件下，将正比例函数的图象向下平移4个单位，求出平移后的直线解析式．
【分析】（1）将（0，0）代入函数解析式即可解决问题．
（2）根据两个一次函数图象平行时，k值相等即可解决问题．
（3）根据“上加下减，左加右减”的平移法则即可解决问题．
【解答】解：（1）因为函数图象经过原点，
所以m﹣3＝0，
解得m＝3，
故m的值为3．
（2）因为函数图象平行于直线y＝3x﹣3，
所以2m+1＝3，
解得m＝1，
所以一次函数解析式为y＝3x﹣2．
函数图象如图所示，
（3）由（1）知，
正比例函数的解析式为y＝7x，
所以此函数图象向下平移4个单位所得函数图象的解析式为y＝7x﹣4．
22．（8分）如图，在▱ABCD中，F是BC的中点，连接AF并延长，交DC的延长线于点E，连接AC，BE．求证：四边形ABEC是平行四边形．
【分析】利用平行四边形的性质、中点的定义以及全等三角形的判定定理推知△ABF≌ECF，得出AF＝EF，即可得出结论．
【解答】证明：∵四边形ABCD是平行四边形
∴AB∥CD，
∴∠BAF＝∠CEF，∠B＝∠ECF，
∵F是BC的中点，
∴BF＝CF，
∴在△ABF与ECF中，，
∴△ABF≌ECF（AAS），
∴AF＝EF，
∴四边形ABEC是平行四边形；
23．（9分）4月23日是“世界读书日”，甲书店在这一天举行了购书优惠活动．
甲书店：“与书相伴，遇见更好地为自己”，一次购书中标价总额不超过80元的按原价计费超过80元的部分5折．以x（单位：元）表示标价总额，y（单位：元）表示应支付金额．
（1）文文购买标价总额50元的书需付款 50 元；购买标价总额100元书需付款 90 元；
（2）求支付金额y关于x的函数解析式，并写出自变量的取值范围；
（3）当天，隔壁的乙书店：“阅读改变生活，共创文明长沙”活动：同样标价的书籍均按标价7折出售；若文文需买250元书，选择哪家书店去购书更省钱？说明你的理由．
【分析】（1）根据题意直接作答即可；
（2）分别写出当0≤x≤80、x＞80时y关于x的函数解析式并写成分段函数的形式即可；
（3）分别计算在甲、乙书店购买应支付的金额并比较大小即可．
【解答】解：（1）∵50＜80，
∴文文购买标价总额50元的书需付款50元；
∵100＞80，
∴购买标价总额100元书需付款80+0.5×（100﹣80）＝90（元）．
故答案为：50，90．
（2）当0≤x≤80时，y＝x；
当x＞80时，y＝80+0.5（x﹣80）＝0.5x+40；
∴y关于x的函数解析式为．
（3）选择甲书店去购书更省钱．理由如下：
在甲书店购买应支付的金额0.5×250+40＝165（元），在乙书店购买应支付的金额0.7×250＝175（元），
∵165＜175，
∴选择甲书店去购书更省钱．
24．（9分）如图，在四边形ABCD中，AB∥DC，AB＝DC，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E．
（1）求证：四边形ABCD是菱形；
（2）若，BD＝2，求CE的长．
【分析】（1）证四边形ABCD是平行四边形，∠BAC＝∠DCA，再证∠DCA＝∠DAC，则AD＝CD，然后由菱形的判定即可得出结论；
（2）由菱形的性质得OA＝OC，OB＝OD＝BD＝1，AC⊥BD，再由勾股定理得OA＝2，则AC＝2OA＝4，然后由菱形面积求出CE的长即可．
【解答】（1）证明：∵AB∥DC，AB＝DC，
∴四边形ABCD是平行四边形，∠BAC＝∠DCA，
∵AC平分∠BAD，
∴∠BAC＝∠DAC，
∴∠DCA＝∠DAC，
∴AD＝CD，
∴平行四边形ABCD是菱形；
（2）解：∵四边形ABCD是菱形，
∴OA＝OC，OB＝OD＝BD＝1，AC⊥BD，
∴∠AOB＝90°，
∴OA＝＝＝2，
∴AC＝2OA＝4，
∵CE⊥AB，
∴S菱形ABCD＝AB•CE＝AC•BD，
即CE＝×4×2，
解得：CE＝，
即CE的长为．
25．（10分）如图，在平面直角坐标系中，函数y＝2x+8的图象分别交x轴、y轴于A、B两点，过点A的直线交y轴正半轴于点M，且点M为线段OB的中点．
（1）求直线AM的函数解析式．
（2）试在直线AM上找一点P，使得S△ABP＝S△AOB，请直接写出点P的坐标．
（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、B、M、H为顶点的四边形是平行四边形？若存在，请直接写出所有点H的坐标；若不存在，请说明理由．
【分析】（1）利用一次函数图象上点的坐标特征可求出点A，B的坐标，由点M为线段OB的中点可得出点M的坐标，根据点A，M的坐标，利用待定系数法即可求出直线AM的函数解析式；
（2）设点P的坐标为（x，x+4），利用三角形的面积公式结合S△ABP＝S△AOB，即可得出关于x的含绝对值符号的一元一次方程，解之即可得出点P的坐标；
（3）设点H的坐标为（m，n），分别以△ABM的三边为对角线，利用平行四边形的性质（对角线互相平分），即可得出关于m，n的方程组，解之即可得出点H的坐标，此题得解．
【解答】解：（1）当x＝0时，y＝2x+8＝8，
∴点B的坐标为（0，8）；
当y＝0时，2x+8＝0，
解得：x＝﹣4，
∴点A的坐标为（﹣4，0）．
∵点M为线段OB的中点，
∴点M的坐标为（0，4）．
设直线AM的函数解析式为y＝kx+b（k≠0），
将A（﹣4，0），B（0，4）代入y＝kx+b，得：，
解得：，
∴直线AM的函数解析式为y＝x+4．
（2）设点P的坐标为（x，x+4），
∵S△ABP＝S△AOB，
∴BM•|xP﹣xA|＝OA•OB，即×4×|x+4|＝×4×8，
解得：x1＝﹣12，x2＝4，
∴点P的坐标为（﹣12，﹣8）或（4，8）．
（3）设点H的坐标为（m，n）．
分三种情况考虑（如图所示）：
①当AM为对角线时，，
解得：，
∴点H1的坐标为（﹣4，﹣4）；
②当AB为对角线时，，
解得：，
∴点H2的坐标为（﹣4，4）；
③当BM为对角线时，，
解得：，
∴点H3的坐标为（4，12）．
综上所述：在坐标平面内存在点H，使以A、B、M、H为顶点的四边形是平行四边形，点H的坐标为（﹣4，﹣4），（﹣4，4）或（4，12）．
26．（10分）在平面直角坐标系xOy中，对于任意两点M（x1，y1），N（x2，y2），定义如下：点M与点N的“直角距离”为|x1﹣x2|+|y1﹣y2|，记作dMN．
例如：点M（1，5）与N（7，2）的“直角距离”dMN＝|1﹣7|+|5﹣2|＝9．
（1）两点P1（﹣1，0）、P2（1，1）中，与原点O的“直角距离”等于1的点是 P1 ；
（2）如图，已知点A（1，0），B（0，1），根据定义可知线段AB上的任意一点与原点O的“直角距离”都等于1．若点P（x，y）与原点O的“直角距离”dOP＝1，即|x﹣0|+|y﹣0|＝1．则当x＝时，点P的坐标为 （﹣，）或（﹣，﹣） ，请你在图中将所有满足条件的点P组成的图形补全；
（3）已知直线y＝kx+3和点C（2，0），若直线y＝kx+3上存在点D，满足dCD＝1，求k的取值范围．
【分析】（1）根据“直角距离”分别计算四个点到原点的距离，即可判断；
（2）根据“直角距离”的定义得|x|+|y|＝1，分四种情况可得四个函数关系式，分别画出即可；
（3）先根据题意可得点C的坐标为（3，0），根据dCD＝1，并由（2）可得：点D在正方形EFMN边上，如图2，通过观察图2可得：k的最大值是过点E的直线，k的最小值是过F，M的直线，代入可得结论．
【解答】解：（1）∵点P1（﹣1，0），P2（1，1），
∴＝|﹣1|+0＝1，＝|1|+|1|＝2，
∴与原点O的“直角距离”等于1的点是P1，
故答案为：P1；
（2）设P（x，y），
∵点P与原点O的“直角距离”dOP＝1，
∴|x|+|y|＝1，
当x＞0，y＞0时，x+y＝1，即y＝﹣x+1，
当x＞0，y＜0时，x﹣y＝1，即y＝x﹣1，
当x＜0，y＞0时，﹣x+y＝1，即y＝x+1，
当x＜0，y＜0时，﹣x﹣y＝1，即y＝﹣x﹣1，
当x＝﹣时，y＝x+1＝﹣+1＝，
当x＝﹣时，y＝﹣x﹣1＝﹣1＝﹣，
∴点P的坐标为（﹣，）或（﹣，﹣），
如图1所示，
故答案为：（﹣，）或（﹣，﹣）；
（3）∵点C的坐标为（2，0），
由（2）可得：dCD＝1，则点D在正方形EFMN边上，如图2，
∴F（1，0），E（2，1），M（2，﹣1），N（3，0），
又∵点D在直线y＝kx+3，又直线y＝kx+3过点（0，3），
由图2可知：当直线y＝kx+b过点E时，通过观察图2可得：k的最大值是过点E的直线，k的最小值是过F，M的直线，
把点E的坐标（2，1）代入y＝kx+3中，2k+3＝1，k＝﹣1，
把点F的坐标（1，0）代入y＝kx+3中，k+3＝0，k＝﹣3，
故k的取值范围是：﹣3≤k≤﹣1．