

2024年中考押题预测卷01(安徽卷)-数学(考试版)A4
展开数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A,B,C,D QUOTE 四个选项,其中只有一个是符合题目要求的.
1.下列各数中,最小的是( )
A.3B.0C.D.
2.某几何体的三视图如图所示,这个几何体是( )
A.B.C.D.
3.2023年合肥经开区GDP达到亿元,连续四年每年跨越一个百亿台阶,其中亿用科学记数法表示为( )
A.B.C.D.
4.下列运算正确的是( )
A.B.C.D.
5.如图,是的外接圆,,则的度数等于( )
A.B.C.D.
6.如图,在等边中,,M为的中点,D,E分别是线段上的动点,,以为边向上作等边,则线段的最小值为( )
A.B.C.D.
7.如图,十一旅游黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进,从D出口离开的概率是( )
A.B.C.D.
8.已知为非零实数,且满足,,则下列结论一定正确的是( )
A.B.
C.D.
9.如图,在矩形中,,点为的中点,以点为圆心,长为半径作弧交于点,再以点A为圆心,长为半径作弧交于点与相交于点,则的值为( )
A.B.C.D.
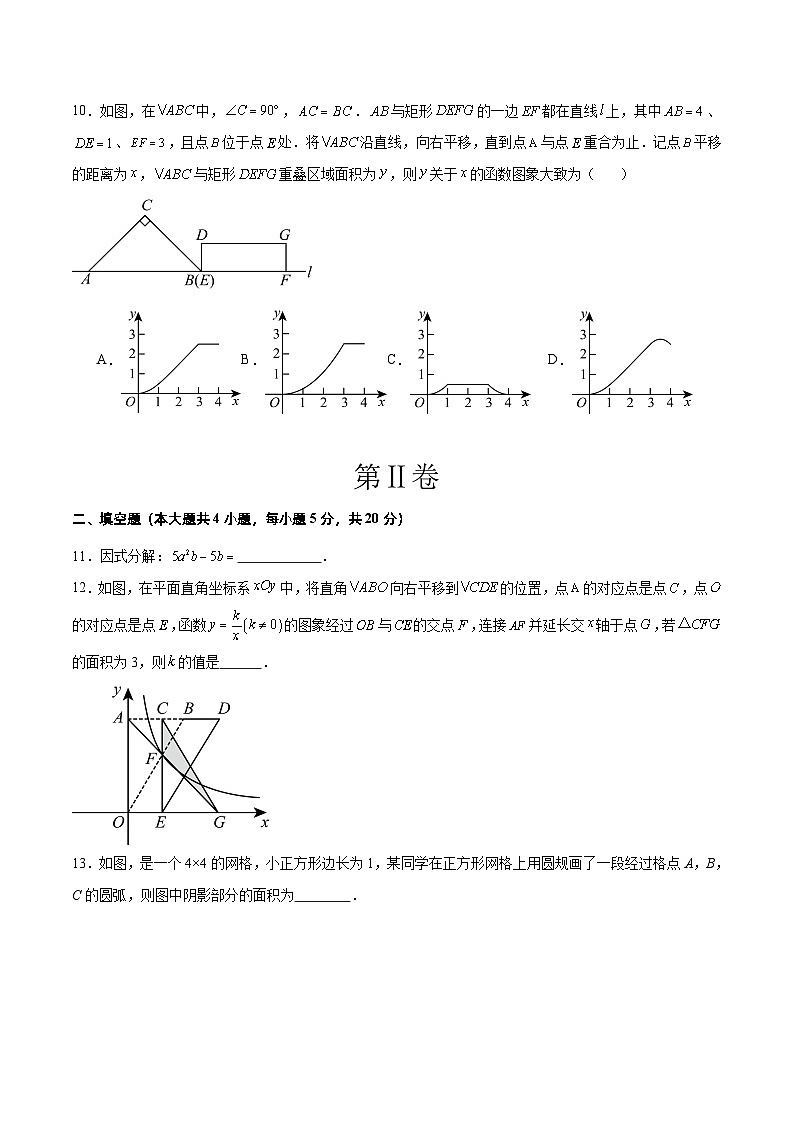
10.如图,在中,,.与矩形的一边都在直线上,其中、、,且点位于点处.将沿直线,向右平移,直到点与点重合为止.记点平移的距离为,与矩形重叠区域面积为,则关于的函数图象大致为( )
A.B.C.D.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分)
11.因式分解: .
12.如图,在平面直角坐标系中,将直角向右平移到的位置,点的对应点是点,点的对应点是点,函数的图象经过与的交点,连接并延长交轴于点,若的面积为3,则的值是 .
13.如图,是一个4×4的网格,小正方形边长为1,某同学在正方形网格上用圆规画了一段经过格点A,B,C的圆弧,则图中阴影部分的面积为 .
14.如图,点E是正方形的边上一点,以所在直线为对称轴折叠,得到,点H为延长线上一点,以所在直线为对称轴折叠,恰好与重合.
(1)的度数为 .
(2)若,则点H到的距离最大为 .
三、(本大题共2小题,每小题8分,满分16分)
15.解不等式组:
16.【观察思考】
如图,春节期间,广场上用红梅花(黑色圆点)和黄梅花(白色圆点)组成“中国结”图案.
【规律总结】
请用含n的式子填空:
(1)第n个图案中黄梅花的盆数为______;
(2)第1个图案中红梅花的盆数可表示为,第2个图案中红梅花的盆数可表示为,第3个图案中红梅花的盆数可表示为,第4个图案中红梅花的盆数可表示为,…;第n个图案中红梅花的盆数可表示为______;
【问题解决】
(3)已知按照上述规律摆放的第n个“中国结”图案中红梅花比黄梅花多68盆,结合图案中红梅花和黄梅花的排列方式及上述规律,求n的值.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点).
(1)将线段先向左平移1个单位长度,再向下平移3个单位长度,得到线段,画出线段;
(2)将线段绕点B顺时针旋转,得到线段,画出线段;
(3)在外找一点P,画出射线,使得平分.
18.数字化阅读凭借其独有的便利性成为了更快获得优质内容的重要途径.近年来,我国数字阅读用户规模持续增长,据统计年我国数字阅读用户规模达亿人,年约为亿人.
(1)求年到年我国数字阅读用户规模的年平均增长率;
(2)按照这个增长率,预计年我国数字阅读用户规模能否达到亿人.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,是的直径,是上两点,且,连接并延长与过点的的切线相交于点,连接.
(1)证明:平分;
(2)若,求的长.
20.如图,是一座南北走向的大桥,一辆汽车在笔直的公路上由北向南行驶,在处测得桥头在南偏东方向上,继续行驶1500米后到达处,测得桥头在南偏东方向上,桥头在南偏东方向上,求大桥的长度.(结果保留整数,参考数据:,,,)
六、(本题满分12分)
21.寒假期间,某校举行学生参加家务劳动视频评比,成绩记为分(),分为四个分数段:,,,.学校从人的参赛视频中随机抽取了部分视频统计成绩,并绘制了统计图表,部分信息如下:
请根据以上信息,完成下列问题:
(1)补全频数分布直方图;
(2)样本成绩的中位数落在第______分数段中;
(3)若分以上(含分)成绩的学生被评为“劳动能手”,根据统计成绩,试估计全校被评为“劳动能手”的学生人数.
七、(本题满分12分)
22.已知抛物线与x轴交于,两点,经过点,与y轴交于点.
(1)求抛物线的函数解析式;
(2)若点M是x轴上位于点A与点B之间的一个动点(含点A与点B),过点M作x轴的垂线分别交抛物线和直线于点E、点F.求线段的最大值.
八、(本题满分14分)
23.如图1,四边形中,,为边上一点,连接,交于点,于点,,,.
(1)求证:;
(2)已知,.
(ⅰ)求的长;
(ⅱ)如图2,连接并延长交于点,连接,求证:.
2024年中考押题预测卷01(南京卷)-数学(考试版)A4: 这是一份2024年中考押题预测卷01(南京卷)-数学(考试版)A4,共6页。
2024年中考押题预测卷01(福建卷)-数学(考试版)A4: 这是一份2024年中考押题预测卷01(福建卷)-数学(考试版)A4,共8页。
2024年中考押题预测卷01(重庆卷)-数学(考试版)A4: 这是一份2024年中考押题预测卷01(重庆卷)-数学(考试版)A4,共8页。












