备考2024年中考数学核心素养专题七 几何图形的新定义问题练习附解析

这是一份备考2024年中考数学核心素养专题七 几何图形的新定义问题练习附解析，共68页。试卷主要包含了选择题，填空题，综合题等内容，欢迎下载使用。
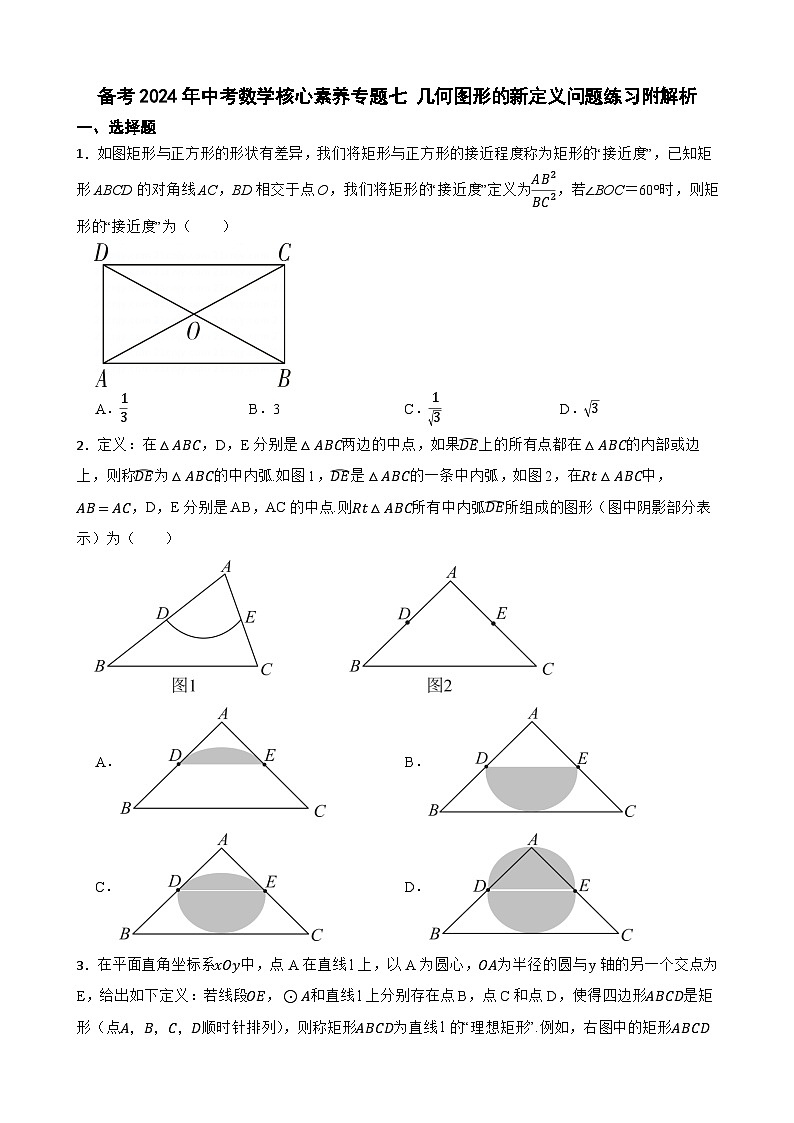
1．如图矩形与正方形的形状有差异，我们将矩形与正方形的接近程度称为矩形的“接近度”，已知矩形ABCD的对角线AC，BD相交于点O，我们将矩形的“接近度”定义为AB2BC2，若∠BOC＝60°时，则矩形的“接近度”为（ ）
A．13B．3C．13D．3
2．定义：在△ABC，D，E分别是△ABC两边的中点，如果DE上的所有点都在△ABC的内部或边上，则称DE为△ABC的中内弧.如图1，DE是△ABC的一条中内弧，如图2，在Rt△ABC中，AB=AC，D，E分别是AB，AC的中点.则Rt△ABC所有中内弧DE所组成的图形（图中阴影部分表示）为（ ）
A．B．
C．D．
3．在平面直角坐标系xOy中，点A在直线l上，以A为圆心，OA为半径的圆与y轴的另一个交点为E，给出如下定义：若线段OE，⊙A和直线l上分别存在点B，点C和点D，使得四边形ABCD是矩形（点A，B，C，D顺时针排列），则称矩形ABCD为直线l的“理想矩形”.例如，右图中的矩形ABCD为直线l的“理想矩形”.若点A(3，4)，则直线y=kx+1(k≠0)的“理想矩形”的面积为（ ）
A．12B．314C．42D．32
4．百度百科这样定义凹四边形：把四边形的某边向两方延长，其他各边有不在延长所得直线的同一旁，这样的四边形叫做凹四边形.关于凹四边形 ABCD （如图），以下结论：
①∠BCD=∠A+∠B+∠D ；②若 AB=AD，BC=CD ，则 AC⊥BD ；③若 ∠BCD=2∠A ，则 BC=CD ；④存在凹四边形 ABCD ，有 AB=CD，AD=BC .其中所有正确结论的序号是（ ）
A．①②B．①②③C．①②④D．①③④
5．我们定义：两边平方和等于第三边平方的2倍的三角形叫做奇异三角形，根据定义：①等边三角形一定是奇异三角形；②在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若Rt△ABC是奇异三角形，则a：b：c＝1：3：2；③如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆ADB的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE＝AD，CB＝CE．则△ACE是奇异三角形；④在③的条件下，当△ACE是直角三角形时，∠AOC＝120°，其中，说法正确的有（ ）
A．①②B．①③C．②④D．③④
二、填空题
6．定义：从一个角的顶点出发，在角的内部引两条射线，如果这两条射线所成的角等于这个角的一半，那么这两条射线所成的角叫做这个角的内半角．已知∠AOB=30°，把一块含有30°角的三角板如图1叠放，将三角板绕顶点O以2度1秒的速度按顺时针方向旋转（如图2）．在旋转一周的过程中，射线OA，OB，OC，OD构成内半角，则旋转时间为 秒．
7．对于平面直角坐标系xOy中的图形M和点P给出如下定义：Q为图形M上任意一点，若P，Q两点间距离的最大值和最小值都存在，且最大值是最小值的5倍，则称点P为图形M的“五分点”.已知点A(2，3)，B(4，6).以点O为圆心，r为半径画圆，若线段AB上存在⊙O的“五分点”，则r的取值范围是 .
8．定义：平面中两条直线 l1 和 l2 相交于点O，对于平面上任意一点M,若p,q分别是M到直线 l1 和 l2 的距离，则称有序非负实数对 (p,q) 是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是 .
9．定义：一个三角形的一边长是另一边长的2倍，这样的三角形叫做“倍长三角形”.若等腰三角形ABC是“倍长三角形”，底边的长为3，则腰AB的长为 .
10．新定义：将一个凸四边形分成一个等腰三角形和一个等腰直角三角形的对角线叫做这个四边形的“等腰直角线”．已知一个直角梯形的“等腰直角线”等于4，它的面积是 ．
11．定义：我们知道，四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的相似对角线，在四边形ABCD中，对角线BD是它的相似对角线，∠ABC=70°，BD平分∠ABC，那么∠ADC= 度
12．定义：以直角三角形的重心为圆心，且与该直角三角形的一边相切的圆叫做这个直角三角形的重切圆.斜边为10，重切圆半径为2的直角三角形的面积是 .
13．我们规定菱形与正方形接近程度称为“接近度”，设菱形相邻两个内角的度数分别为α°，β°，将菱形的“接近度”定义为|α−β|，于是|α−β|越小，菱形越接近正方形.
①若菱形的一个内角为80°，则该菱形的“接近度”为 ；
②当菱形的“接近度”等于 时，菱形是正方形.
14．定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系xOy中，矩形OABC的边OA＝3，OC＝4，点M（2，0），在边AB存在点P，使得△CMP为“智慧三角形”，则点P的坐标为： ．
15．定义：有一个圆分别和一个三角形的三条边各有两个交点，截得的三条弦相等，我们把这个圆叫作“等弦圆”，现在有一个斜边长为6的等腰直角三角形，当等弦圆最大时，这个圆的半径为 .
三、综合题
16．定义：有一组对角之差为90°的四边形为美好四边形.
（1）如图①，△ABC中，∠A＝2∠C，点D，E分别在AB，AC上，AD＝AE，求证：四边形DBCE为美好四边形；
（2）请在图②，图③中分别画一个以AB为边且顶点在格点的美好四边形ABCD；
（3）在（1）的条件下，若DE经过△ABC的内心，BD＝4，CE＝7，求DE的长.
17．我们定义：连接凸四边形一组对边中点的线段叫做四边形的“准中位线”.
（1）概念理解：如图1，四边形ABCD中，F为CD的中点，∠ADB＝90°，E是AB边上一点，满足DE＝AE，试判断EF是否为四边形ABCD的准中位线，并说明理由.
（2）问题探究：如图2，△ABC中，∠ACB＝90°，AC＝6，BC＝8，动点E以每秒1个单位的速度，从点A出发向点C运动，动点F以每秒6个单位的速度，从点C出发沿射线CB运动，当点E运动至点C时，两点同时停止运动.D为线段AB上任意一点，连接并延长CD，射线CD与点A，B，E，F构成的四边形的两边分别相交于点M，N，设运动时间为t.问t为何值时，MN为点A，B，E，F构成的四边形的准中位线.
（3）应用拓展：如图3，EF为四边形ABCD的准中位线，AB＝CD，延长FE分别与BA，CD的延长线交于点M，N，请找出图中与∠M相等的角并证明.
18．定义：有两个相邻内角和等于另两个内角和的一半的四边形称为对半四边形，这两个角的夹边称为对半线．
（1）如图1，在对半四边形ABCD中，∠A+∠B＝12（∠C+∠D），求∠A与∠B的度数之和；
（2）如图2，O为锐角△ABC的外心，过点O的直线交AC，BC于点D，E，∠OAB＝30°，求证：四边形ABED是对半四边形；
（3）如图3，在△ABC中，D，E分别是AC，BC上一点，CD＝CE＝3，CE＝3EB，F为DE的中点，∠AFB＝120°，当AB为对半四边形ABED的对半线时，求AC的长．
19．定义：若圆内接三角形是等腰三角形，我们就称这样的三角形为“圆等三角形”．
（1）如图1，AB是⊙O的一条弦（非直径），若⊙O在上找一点C，使得△ABC是“圆等三角形”，则这样的点C能找到 个．
（2）如图2，四边形ABCD是⊙O的内接四边形，连结对角线BD，△ABD和△BCD均为“圆等三角形”，且AB=AD．
①当∠A=140°时，求∠ADC的度数；
②如图3，当∠A=120°，AB=6时，求阴影部分的面积．
20．综合与实践
新定义：我们把两个面积相等但不全等的三角形叫做积等三角形.
（1）【初步尝试】如图1，已知Rt△ABC中，∠C=90°，AB=5，BC=4，P为AC上一点，当AP= 时，△ABP与△CBP为积等三角形；
（2）【理解运用】如图2，△ABD与△ACD为积等三角形；若AB=3，AC=5，且线段AD的长度为正整数，求AD的长；
（3）【综合应用】如图3，已知Rt△ABC中，∠ACB=90°，分别以AC，AB为边向外作正方形ABDE和正方形ACFG，连接EG，求证：△AEG与△ABC为积等三角形.
21．定义：有一组对角互补的四边形叫做“对补四边形”，例如，四边形 ABCD 中，若 ∠A+∠C=180° 或 ∠B+∠D=180° ，则四边形 ABCD 是“对补四边形”.
（1）（概念理解）
如图1，四边形 ABCD 是“对补四边形”.
①若 ∠A：∠B：∠C=3：2：1 ，则 ∠D= ；
②若 ∠B=90° .且 AB=3，AD=2 时.则 CD2−CB2= ；
（2）（拓展提升）
如图，四边形 ABCD 是“对补四边形”，当 AB=CB ，且 ∠EBF=12∠ABC 时，图中 AB，CF，EF 之间的数量关系是 ，并证明这种关系；
（3）（类比应用）
如图3，在四边形 ABCD 中， AB=CB，BD 平分 ∠ADC ；
①求证：四边形 ABCD 是“对补四边形”；
②如图4，连接 AC ，当 ∠ABC=90° ，且 S△ACDS△ABC=12 时，求 tan∠ACD 的值.
22．定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形．
根据以上定义，解决下列问题：
（1）判断正方形 “直等补”四边形；菱形 “直等补”四边形.（填“是”或“不是”）
（2）如图1，在所给的网格中，画出符合条件的“直等补”四边形AECF；
（3）如图2，已知四边形ABCD是“直等补”四边形，AB＝BC＝5，CD＝1，AD＞AB，点B到直线AD的距离为BE．
①求BE的长；
②若M、N分别是AB、AD边上的动点，求△MNC周长的最小值．
23．在平面直角坐标系xOy中，对于线段AB与直线l：y=kx+b，给出如下定义：若线段AB关于直线l的对称线段为A'B'(A'，B'分别为点A，B的对应点)，则称线段A'B'为线段AB的“[k，b]关联线段”．
已知点A(1，1)，B(1，−1)．
（1）线段A'B'为线段AB的“[1，b]关联线段”，点A'的坐标为(2，0)，则A'B'的长为 ，b的值为 ；
（2）线段A'B'为线段AB的“[k，0]关联线段”，直线l1经过点C(0，2)，若点A'，B'都在直线l1上，连接OA'，求∠COA'的度数；
（3）点P(−3，0)，Q(−3，3)，线段A'B'为线段AB的“[k，b]关联线段”，且当b取某个值时，一定存在k使得线段A'B'与线段PQ有公共点，直接写出b的取值范围．
24．新定义：垂直于图形的一边且等分这个图形面积的直线叫作图形的等积垂分线，等积垂分线被该图形截的线段叫做等积垂分线段.
问题探究：
（1）如图1，等边△ABC边长为3，垂直于BC边的等积垂分线段长度为 ；
（2）如图2，在△ABC中，AB=8，BC=63，∠B=30°，求垂直于BC边的等积垂分线段长度；
（3）如图3，在四边形ABCD中，∠A=∠C=90°，AB=BC=6，AD=3，求出它的等积垂分线段长.
25．在平面直角坐标系中，给出如下定义：P为图形M上任意一点，如果点P到直线EF的距离等于图形M上任意两点距离的最大值时，那么点P称为直线EF的“伴随点”．
例如：如图1，已知点A(1，2)，B(3，2)，P(2，2)在线段AB上，则点P是直线EF：x轴的“伴随点”．
（1）如图2，已知点A(1，0)，B(3，0)，P是线段AB上一点，直线EF过G(−1，0)，T(0，33)两点，当点P是直线EF的“伴随点”时，求点P的坐标；
（2）如图3，x轴上方有一等边三角形ABC，BC⊥y轴，顶点A在y轴上且在BC上方，OC=5，点P是△ABC上一点，且点P是直线EF：x轴的“伴随点”．当点P到x轴的距离最小时，求等边三角形ABC的边长；
（3）如图4，以A(1，0)，B(2，0)，C(2，1)为顶点的正方形ABCD上始终存在点P，使得点P是直线EF：y=−x+b的“伴随点”．请直接写出b的取值范围．
26．定义：对多边形进行折叠，若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形，则这样的四边形称为镶嵌四边形．
（1）如图1，将△ABC纸片沿中位线EH折叠，使点A落在BC边上的D处，再将纸片分别沿EF，HG折叠，使点B和点C都与点D重合，得到双层四边形EFGH，则双层四边形EFGH为 形．
（2）▱ABCD纸片按图2的方式折叠，折成双层四边形EFGH为矩形，若EF=5，EH=12，求AD的长．
（3）如图3，四边形ABCD纸片满足AD∥BC，ADb>a>0，
∴2c2>a2+b2，2a25=CF，
故不符合意.
故答案为：24.
【分析】①设圆与AC相切于点G，I为Rt△ABC的中线AF与BE的交点，连接EF，则EF∥AB，EF=12AB，由平行于三角形一边的直线，截其它两边的延长线，所截的三角形与原三角形相似得△EFI∽△BAI，由相似三角形对应边成比例得AIAF=23，由切线的性质得∠AGI=90°，判断出IG∥BC，推出△AGI∽△ACF，由相似三角形对应边成比例得IGCF=AIAF=23，据此可得CF的长，在Rt△ACB中根据勾股定理算出AC，进而根据三角形面积计算公式即可算出△ABC的面积；②设⊙I与AB相切于点D，过点C作CG⊥AB题意于点G，结合切线的性质可判断出ID∥CG，由平行于三角形一边的直线，截其它两边，所截的三角形与原三角形相似得△FID∽△FCG，由相似三角形对应边成比例得IDCG=FIFC=13，进而结合直角三角形斜边上的中线等于斜边的一半得出CG=3ID=6＞5=CF，根据垂线段最短可得此种情况不符合题意.
13．【答案】20；0
【解析】【解答】解：∵菱形相邻两个内角的度数和为180°，
∴α+β=180，即80+β=180，
解得：β=100
∴该菱形的“接近度”为|α−β|=|80−100|=20；
∵四个角都为直角的菱形是正方形，
∴当α=β=90时，菱形是正方形，
∴|α−β|=0时，菱形是正方形.
故答案为：20，0.
【分析】根据菱形的性质结合题意可得80+β=180，求出β的度数，然后求出|α-β|的值即为该菱形的“接近度”，由正方形的性质可得当α=β=90时，菱形为正方形，同理可求出“接近度”.
14．【答案】(3，12)或(3，1)或(3，3)
【解析】【解答】解：由题可知，“智慧三角形”是直角三角形，∠CPM=90°或∠CMP=90°
设点P(3，a)，则AP=a，BP=4-a
①若∠CPM=90°，在Rt△BCP中，
CP2=BP2+CB2=9+(4−a)2
在Rt△MPA中，MP2=MA2+AP2=1+a2
在Rt△MCP中，CM2=MP2+CP2=9+(4−a)2+1+a2=2a2−8a+26
又∵CM2=OM2+CO2=20
∴2a2-8a+26=20
即(a-3)(a-1)=0
解得a=3或a=1
∴P(3，3)或(3，1)
②若∠CMP=90°，在Rt△BCP中
CP2=BP2+CB2=9+(4−a)2
在Rt△MPA中，MP2=MA2+AP2=1+a2
∵CM2=OM2+CO2=20
在Rt△MCP中，CM2+MP2=CP2=20+1+a2=9+(4−a)2
即a=12
∴P(3，12)
综上所述，点P的坐标为(3，12)或(3，1)或(3，3)
故答案为：(3，12)或(3，1)或(3，3).
【分析】由题可知，“智慧三角形”是直角三角形，∠CPM=90°或∠CMP=90°，设点P(3，a)，则AP=a，BP=4-a，进而分类讨论：①若∠CPM=90°，②若∠CMP=90°，从而运用勾股定理结合题意即可求解。
15．【答案】6−32
【解析】【解答】解：如图，
∵圆与三角形的三条边都有两个交点，截得的三条弦相等，
∴圆心O就是三角形的内心，
∴当⊙O过C时，且在等腰直角△ABC的三边上截得的弦相等，即CG＝CF＝DE，此时⊙O最大，
过点O分别作弦CG、CF、DE的垂线，垂足分别为P、N、M，连接OC、OA、OB，
∵CG＝CF＝DE，
∴OP＝OM＝ON，
∵∠C＝90°，AB＝6，AC＝BC，
∴AC＝BC＝22×6=32
∵S△AOC＋S△BOC＋S△AOB＝S△ABC，
∴12AC⋅OP＋12BC⋅ON＋12AB⋅OM＝S△ABC＝12AC⋅BC，
设OM＝x，则OP＝ON＝x，
∴32x+32x+6x=32×32，
解得：x＝32−3，
即OP＝ON＝32−3，
在Rt△CON中，OC=2ON=6−32，
故答案为：6−32.
【分析】根据题意画出相应的图形，易得圆心O就是三角形的内心，当⊙O过C时，且在等腰直角△ABC的三边上截得的弦相等，即CG＝CF＝DE，此时⊙O最大，过点O分别作弦CG、CF、DE的垂线，垂足分别为P、N、M，连接OC、OA、OB，根据同圆中等弦的圆心距相等得OP＝OM＝ON，根据等腰直角三角形的性质求出AC、BC的长，进而根据S△AOC＋S△BOC＋S△AOB＝S△ABC，建立方程，求出OP的长，最后再根据等腰直角三角形的性质即可求出OC的长，从而问题得以解决.
16．【答案】（1）证明：设∠C=x，则∠A=2x，
∵AD=AE，故∠ADE=∠AED=90°−x，
即∠BDE=90°+x，
故∠BDE−∠C=90°，
∴四边形DBCE为美好四边形；
（2）解：依据题意，图形见图1−图4（答案不唯一），
（3）解：过点A作AP⊥AD于点P，
∵AD=AE，故AP是∠BAC的平分线且PD=PE=12ED，
∵DE经过ΔABC的内心，故点P是ΔABC的内心，
连接BP、CP，则BP、CP分别为∠ABC、∠ACB的平分线，
设∠DAP=∠PAE=α，∠DBC=∠PBC=β，∠ECP=∠PCB=γ，
∵ΔABC的内角和为180°，即2α+2β+2γ=180°，
而x=2γ，则α+β=90°−x，
则∠BPC=180°−α−β=90°+x=∠BDE，
∵∠BDE=180°−∠DBP−∠DPB，∠BDC=180°−∠DPB−∠EPC，
∴∠DPB=∠EPC，
∵AD=AE，故∠ADE=∠AED，则∠BDP=∠CEP，
∵ΔDBP∽ΔEPC，
∴BDEP=DPCE，即EP⋅PD=BD⋅EC=4×7=28，
而EP=PD，
故EP=PD=27=12DE，
∴DE=47.
【解析】【分析】（1）设∠C=x，则∠A=2x，由等腰三角形的性质以及内角和定理可得∠ADE=∠AED=90°-2x，根据邻补角的性质可得∠BED=90°+x，则∠BDE-∠C=90°，据此证明；
（2）根据“ 美好四边形 ”的概念进行作图；
（3）过点A作AP⊥DE于点P，根据等腰三角形的性质可得AP平分∠BAC且PD=PE，易得点P为△ABC的内心，连接BP、CP，则BP、CP分别为∠ABC、∠ACB的平分线，设∠DAP=∠PAE=α，∠DBC=∠PBC=β，∠ECP=∠PCB=γ，由内角和定理可推出∠BPC=∠BDE，∠DPB=∠EPC，证明△DBP∽△EPC，然后根据相似三角形的性质进行计算.
17．【答案】（1）解：∵DE＝AE，
∴∠EDA＝∠EAD，
∵∠EDA＋∠EDB＝90°，∠EAD＋∠ABD＝90°，
∴∠EDB＝∠ABD，
∴DE＝BE，
∴AE＝BE，
∵F为CD的中点，
∴EF为四边形ABCD的准中位线
（2）解：当MN为点A，B，F，E构成的四边形的准中位线时，
①如图①，当0≤t≤ 43 时，则需满足EF∥AB且M（D）为AB的中点，
∴6−t6=6t8 ，
解得：t＝ 1211 ；
②当 43 ＜t≤6时，需满足BE∥AF且M为AF的中点，
∴6−t6=86t ，
解得：t＝2或t＝4，
综上所述，当t＝ 1211 或t＝2或t＝4时，MN为点A，B，E，F构成的四边形的准中位线；
（3）解：∠M＝∠CNF，
理由：连接BD，取BD的中点H，连接EH，FH，
∵E，H分别为AD，BD的中点，
∴EH∥AB，EH＝ 12 AB，
∴∠M＝∠HEF，
∵F，H分别为BC，BD的中点，
∴FH∥CD，FH＝ 12 CD，
∴∠CNF＝∠HFE，
∵AB＝CD，
∴HE＝HF，
∴∠HEF＝∠HFE，
∴∠M＝∠CNF.
【解析】【分析】（1）根据等腰三角形的性质得到∠EDA＝∠EAD，根据余角的性质得到∠EDB＝∠ABD，得到AE＝BE，于是得到结论；（2）当MN为点A，B，F，E构成的四边形的准中位线时，①如图①，当0≤t≤ 43 时，②当 43 ＜t≤6时，根据题意列方程即可得到结论；（3）连接BD，取BD的中点H，连接EH，FH，根据三角形的中位线定理得到EH∥AB，EH＝ 12 AB，求得∠M＝∠HEF，又根据三角形的中位线定理得到FH∥CD，FH＝ 12 CD，求得∠CNF＝∠HFE，于是得到结论.
18．【答案】（1）解：由四边形内角和为360°，可得∠A+∠B+∠C+∠D＝360°，
则∠A+∠B+2（∠A+∠B）＝360°，
∴∠A+∠B＝120°
（2）证明：如图2，连接OC，由三角形外心的性质可得，OA＝OB＝OC，
∴∠OAB＝∠OBA＝30°，∠OCA＝∠OAC，∠OCE＝∠OBC，
∴∠ACB＝（180°-30°-30°）÷2＝60°，
则∠CAB+∠CBA＝120°，
在四边形ABED中，∠CAB+∠CBA＝120°，
则另两个内角之和为240°，
∴四边形ABED为对半四边形；
（3）解：若AB为对半线，则∠CAB+∠CBA＝120°，
∴∠C＝60°，
又∵CD＝CE，
∴△CDE为等边三角形，
∵∠CDE＝CED＝60°，DE＝DC＝3，
∴∠ADF＝∠FEB＝120°，
∵∠AFB＝120°，
∴∠DFA+∠EFB＝60°，
又∵∠DAF+∠DFA＝60°，
∴∠DAF＝∠EFB，
∴△ADF∽△FEB，
∴ADFE=DFEB
∵CE＝DE＝3，CE＝3BE，F是DE的中点，
∴BE＝1，DF＝EF＝32，
∴AD32＝321，
∴AD＝94，
∴CA＝CD+AD＝3+94＝214．
【解析】【分析】（1）由四边形内角和为360°可得∠A+∠B+∠C+∠D＝360°，由已知条件可知∠A+∠B＝12(∠C+∠D)，则∠A+∠B+2(∠A+∠B)＝360°，化简即可；
（2）连接OC，由三角形外心的性质可得OA＝OB＝OC，根据等腰三角形的性质可得∠OAB=∠OBA=30°，∠OCA=∠OAC，∠OCE=∠OBC，结合内角和定理可求出∠ACB的度数，然后求出∠CAB+∠CBA的度数，结合四边形内角和为360°可得另两个内角之和为240°，据此证明；
（3）若AB为对半线，则∠CAB+∠CBA＝120°，由内角和定理可得∠C＝60°，易得△CDE为等边三角形，则∠CDE＝CED＝60°，DE＝DC＝3，∠ADF＝∠FEB＝120°，由两角对应相等的两个三角形相似可得△ADF∽△FEB，由已知条件可得BE＝1，DF＝EF＝32，利用相似三角形的性质可得AD，然后根据CA＝CD+AD进行计算.
19．【答案】（1）4
（2）解：①∵四边形ABCD是⊙O的内接四边形，∠A=140°，
∴∠C=180°−∠A=40°，
①当BC=BD时，∠BDC=∠C=40°，
∵AB=AD，
∴∠ADB=180°−140°2=20°，
∴∠ADC=∠ADB+∠BDC=60°，
②当BD=DC时，∠C=∠DBC=40°，
∴∠BDC=180°−∠DBC−∠C=100°，
∴∠ADC=∠ADB+∠BDC=120°，
③当BC=CD时，∠BDC=180°−∠C2=70°，
∴∠ADC=∠ADB+∠BDC=90°，
综上所述，∠ADC的度数可能为：90°，120°，60°，
②连接OA、OB、OC，过点E作OE⊥BC，如下图：
∵四边形ABCD是⊙O的内接四边形，∠A=120°，
∴∠BCD=180°−∠A=60°，
∵△BCD均为“圆等三角形”，
∴△BCD为等边三角形，
∴∠BOC=2∠BDC=120°，
∵AB=AD，
∴∠AOB=12∠BOD=60°，
∵BO=AO，
∴△AOB为等边三角形，
∴OB=AB=6，
在Rt△BOE中，OE=12OB=3，BE=3OE=33，
∴S△BOC=12×2×33×3=93，
扇形BOC的面积：120°360°×π×62=12π，
∴阴影部分的面积为：12π−93.
【解析】【解答】解：（1）图下图：
∴这样的点C能找到4个，
故答案为：4.
【分析】（1）根据圆等三角形的定义，即可求解；
（2）①根据圆内接四边形和已知条件求出∠C的度数，再分三种情况讨论，①当BC=BD时，②当BD=DC时，③当BC=CD时，分别根据三角形内角和定理即可求解；
②连接OA、OB、OC，过点E作OE⊥BC，根据圆内接四边形和已知条件求出∠BCD的度数，根据圆等三角形的定义得到△BCD为等边三角形，根据圆周角定理得到∠BOC的度数，即可证明△AOB为等边三角形，根据含30°角的直角三角形求出OE和BE的长，进而求出△BOC的面积和扇形BOC的面积，即可求出阴影部分面积.
20．【答案】（1）1.5
（2）解：如图，过点C作CE∥AB，交AD的延长线于点E，
∵△ABD与△ACD为积等三角形，
∴BD=CD，
∵AB∥EC，
∴∠BAD=∠E，
∵∠ADB=∠EDC，
∴△ADB≅△EDC(AAS)，
∴AD=DE，AB=EC=3，
∴AE=2AD，
∵AC=5，
∵AC−CE