陕西省西安国际港务区铁—中陆港初级中学2023-2024学年下学期七年级期中考试数学试题

这是一份陕西省西安国际港务区铁—中陆港初级中学2023-2024学年下学期七年级期中考试数学试题，共4页。试卷主要包含了选择题，填空题，解答题，能力提升题等内容，欢迎下载使用。

(满分: 100+20分 时间: 90分钟)
一、选择题(每题3分、共30分)
1、计算 -2024⁰=
A. 1 B 0 C. -1 D. -2024
2、若一个角的补角为30°，则这个角等于( )
A. 30° B. 60° C. 120° D. 150°
3、芯片技术作为当今社会信息化的核心基础 其在各个领域的应用已经愈发广泛.国产芯片从原来的“卡脖子”到现在不断发展，国产芯片制造商SMIC已经推出了7纳米(其中1纳米=0.000000001米)和5 纳米的芯片，中芯国际和华虹半导体等公司也在尝试开发7纳米芯片.其中7纳米用科学记数法表示为( )
A. 0.7×10⁻⁹米 B.7×10⁻⁹米 C.7×10⁻⁸米 D.7×10⁻⁷米
4、下列长度的三条线段能组成三角形的是( )
A. 2、3、5 B. 9、4. 5 ₢. 2、2、5 D. 3、4、8
5、第四届铁一陆港运动会男子100米决赛在风雨操场上进行，随着一声发令枪响，健儿们像离弦的箭一般冲了出去.看着赛场上激烈的角逐，求知小组的同学也展开了激烈的讨论：声音传播的速度和什么有关系呢?好学的小陆同学利用五一假期查阅资料，找到声音在空气中传播的速度与空气温度关系的一些数据(如下表)：
下列说法错误的是( )
A.在这个变化中，自变量是温度，因变量是声速
B.温度越高，声速越快
C. 当空气温度为20℃时, 声音5s可以传播1740m
D. 当温度每升高10℃, 声速增加6m/s
6、如图, 将长方形纸条ABCD折叠, 折痕为EF, 折叠后点C、D分别落在点C', D'处,D'E与BF交于点G, 若∠BGD'=28°, 则∠FED'的度数是( )
A. 28° B. 62° C. 75° D. 76°
7、如图, ∠A=∠D, AC=DF, 下列条件中不能判断△ABC≌△DEF的是( )
A. AB=DE B. EF=BC C. ∠B=∠E D. ∠C=∠F
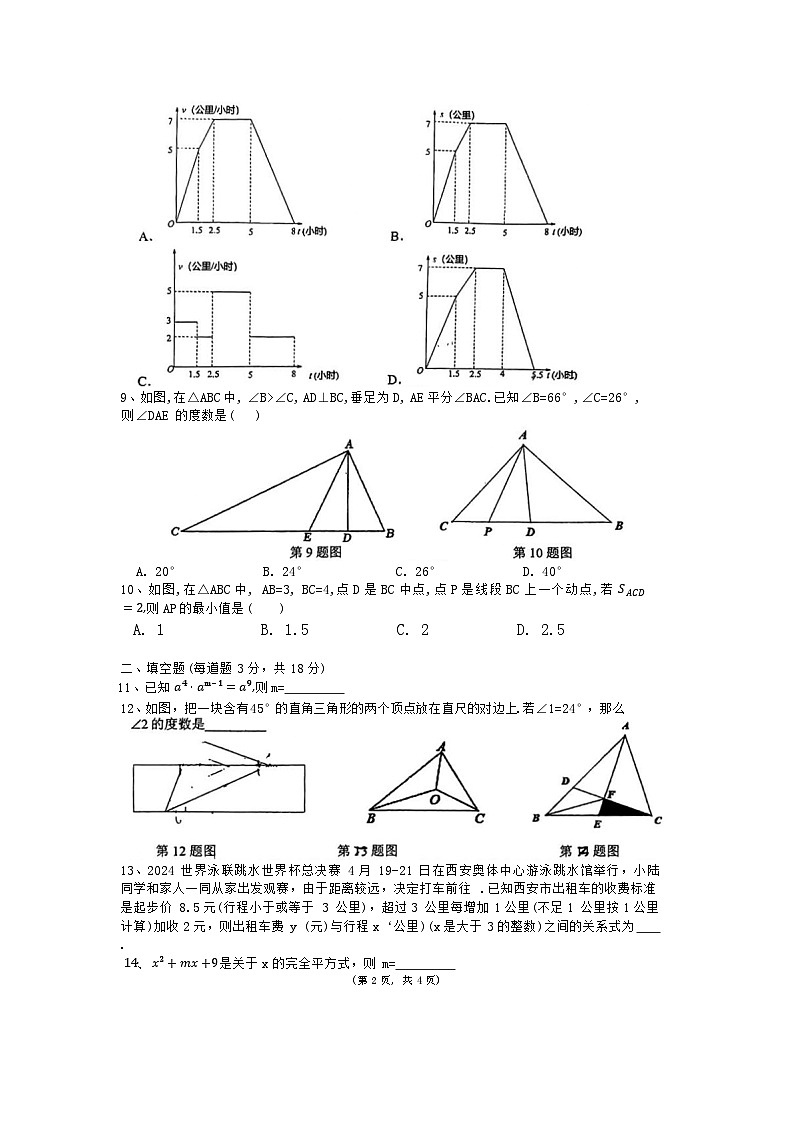
8、4月19日，我校两一年级开展了“徒步春光”活动，8：30从学校出发，前 1.5 小时匀速行进了5公里，后来遇到道路施工，整体放缓速度，1小时匀速向前行进了2公里后，到达浐灞国家湿地公园，各班随即开展了丰富多彩的户外研学活动，13：30开启返程，用时3小时匀速回到学校.本次活动既是“第三课堂”的践行，将课本知识与社会实践相连，更磨练了意志，挑战了自我，根据以上信息，判断下列图象正确的是( )
(第1页, 共4页)温度/℃
-20
-10
0
10.
20
30
声速/m/s
318
324
330
336
342
348
9、如图,在△ABC中, ∠B>∠C, AD⊥BC,垂足为D, AE平分∠BAC.已知∠B=66°,∠C=26°, 则∠DAE 的度数是( )
A. 20° B. 24° C. 26° D. 40°
10、如图,在△ABC中, AB=3, BC=4,点D是BC中点,点P是线段BC上一个动点,若 SACD=2,则AP的最小值是( )
A. 1 B. 1.5 C. 2 D. 2.5
二、填空题(每道题3分，共18分)
11、已知 a⁴⋅aᵐ⁻¹=a⁹,则m=
12、如图，把一块含有45°的直角三角形的两个顶点放在直尺的对边上.若∠1=24°，那么
13、2024 世界泳联跳水世界杯总决赛 4月 19-21 日在西安奥体中心游泳跳水馆举行，小陆同学和家人一同从家出发观赛，由于距离较远，决定打车前往.已知西安市出租车的收费标准是起步价 8.5元(行程小于或等于 3 公里)，超过3 公里每增加1公里(不足1 公里按1公里计算)加收2元，则出租车费y (元)与行程x‘公里)(x是大于3的整数)之间的关系式为 .
14、x²+mx+9是关于x的完全平方式，则m=
(第2页, 共4页) 14、x²+mx+9是关于x的完全平方式，则m-
15、如图, O为△ABC三条角平分线的交点,连接OA、OB、OC, 若∠BOC=120°,则∠BAC= .
16、如图, D、E分别是△ABC边AB、BC上的点, AD=2BD, BE=CE, 连接AE、CD交于点F, 连接BF, 若△BDF的面积为4, 则阴影部分的面积= .
三、解答题(共8小题，共52分)
17、(6分)利用整式乘法公式简便计算：
12024²-2023×2025; (2) 199².
18、(12分) 计算:
1-12-2+-42024×-142023; 2-2a²³+6a⁸+2a²;
3x-y²-x-yx+2y; 43a-b-13a-b+1.
19、(5分) 如图, 利用尺规, 过点C作直线CD, 使: CD∥AB.(尺规作图要求保留作图痕迹，不写作法)
20、 (5分)先化简,再求值: 3x+y2+x+2yx-2y+3y2÷-12x,其中 x=2,y=-12.
21、(5分)如图, △ABC中, D为AC边上一点, 过D作DE∥AB,交BC于E; F为AB边上一点,连接DF并延长, 交CB的延长线于G, ∠DFA=∠A. 求证: DE平分∠CDF.
22、(5分)已知动点P 以每秒1cm的速度沿如图所示的边框按从 B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图所示，若 AB=3cm,试回答下列问题.
(1)此题的自变量是 ，因变量是 ；
(2) 如图甲, BC的长是 cm;
(3)如图乙,图中的a是 ,b是 .
23、(6分)如图, 在. Rt△ABC中, ∠ABC=90°,点D在BC的延长线上，且 BD=AB.过点 B 作 BE⊥AC,与BD的垂线DE交于点E.
(1) 求证: △ABC≅△BDE;
(2)若 AB=12,DE=5,求CD的长.
(第3页, 共4页)
24、(8分)如图1,已知直线EF与直线AB交于点E,与直线CD交于点F , EM 平分 ∠AEF交直线CD于点M，且 ∠FEM=∠FME.
(1)试判断直线AB与CD的位置关系，并说明理由；
(2)点G是射线MD上的一个动点(不与点M, F 重合), EH平分. ∠FEG交直线CD于点H, 过点H作HN∥EM 交直线AB于点N. 设. ∠EHN=α,∠EGF=β.
①如图2，当点G 在点F的右侧，且 α=48°时,求β的值;
②当点G在运动过程中，α和β之间有怎样的数量关系?请直接写出结论.
四、能力提升题(共5小题，共20分)
1、 已知 2024-a2+a-20232=12, 则(2024-a)(a-2023)= .
2、如图，已知方格纸中是4个相同的正方形，则 ∠1+∠2-∠3=.
3、 已知 ∠A=30°,∠B的一条边和∠A的一边平行，∠B另一条边和∠A的另一条边垂直，则 ∠B=.
4、 已知△ABC三边分别是a、b、c, 化简| |a+b-c|-|c-a+b|+|b-a-c|=.
5、如图, △ABC中, D为BC的中点. 若AB=5, AC=4, 则AD的取值范围 .
(第4页, 共4页)