2024年陕西省西安市碑林区西安工业大学附属中学中考三模数学试题（原卷版+解析版）

这是一份2024年陕西省西安市碑林区西安工业大学附属中学中考三模数学试题（原卷版+解析版），文件包含2024年陕西省西安市碑林区西安工业大学附属中学中考三模数学试题原卷版docx、2024年陕西省西安市碑林区西安工业大学附属中学中考三模数学试题解析版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。
温馨提示：请同学们考试结束后将试卷和答题卡一并交回．
第一部分（选择题 共24分）
一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）
1. 某天某港口最高水位为1m，最低水位为m，该天最高水位与最低水位的差是（ ）
A. 1mB. mC. 3mD. m
2. 中国茶文化源远流长，在下列有关茶的标识中，是轴对称图形的是（ ）
A. B. C. D.
3. 如图，直线，C在直线m上，过点C作，若，则为（ ）
A. B. C. D.
4. 下列运算，与计算结果相同的是（ ）
A B. C. D.
5. 正比例函数的图象经过、两点，过点的一次函数的图象随的增大而减小，则等于（ ）
A. B. C. D.
6. 如图，正方形中，E为中点，，，交于O，则的度数为（ ）
A. B. C. D.
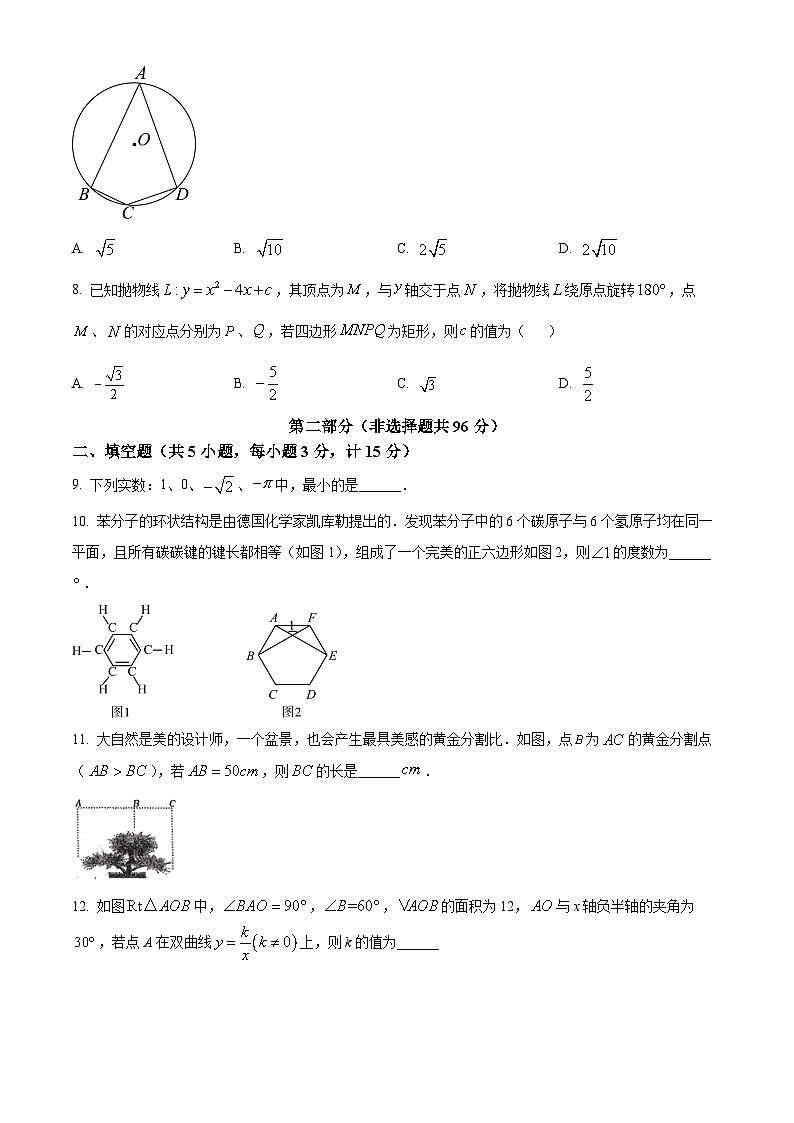
7. 如图，四边形内接于，，，，则的半径为（ ）

A. B. C. D.
8. 已知抛物线，其顶点为，与轴交于点，将抛物线绕原点旋转，点、的对应点分别为、，若四边形为矩形，则的值为（ ）
A. B. C. D.
第二部分（非选择题共96分）
二、填空题（共5小题，每小题3分，计15分）
9. 下列实数：1、0、、中，最小的是______．
10. 苯分子的环状结构是由德国化学家凯库勒提出的．发现苯分子中的6个碳原子与6个氢原子均在同一平面，且所有碳碳键的键长都相等（如图1），组成了一个完美的正六边形如图2，则的度数为______．
11. 大自然是美的设计师，一个盆景，也会产生最具美感的黄金分割比．如图，点为的黄金分割点（），若，则的长是______．
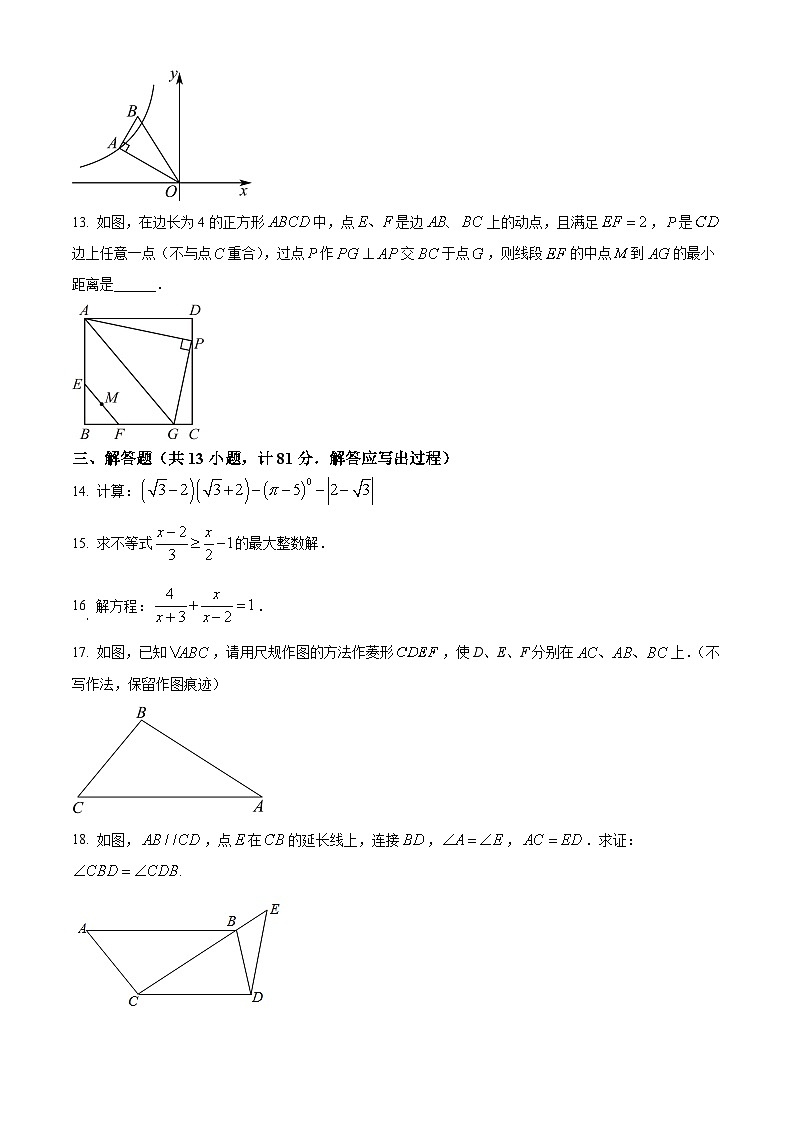
12. 如图中，，，的面积为12，与x轴负半轴的夹角为，若点A在双曲线上，则k的值为______
13. 如图，在边长为4的正方形中，点是边上的动点，且满足，是边上任意一点（不与点重合），过点作交于点，则线段的中点到的最小距离是______．
三、解答题（共13小题，计81分．解答应写出过程）
14. 计算：
15. 求不等式的最大整数解．
16 解方程：．
17. 如图，已知，请用尺规作图的方法作菱形，使D、E、F分别在上．（不写作法，保留作图痕迹）

18. 如图，，点在的延长线上，连接，，．求证：
19. 读诗词解题：（通过列方程式，算出周瑜去世时的年龄）
大江东去浪淘尽，千古风流数人物；
而立之年督东吴，早逝英年两位数；
十位恰小个位三，个位平方与寿符；
哪位学子算得快，多少年华属周瑜？
20. “春雨惊春清谷天，夏满芒夏暑相连；秋处露秋寒霜降，冬雪雪冬小大寒”．“二十四节气”是中华上古农耕文明的产物，蕴含了中华民族悠久的文化内涵和历史沉淀．小明购买了四张邮票，分别是“立春、立夏、秋分、大寒”，现将它们背面朝上放在桌面上（邮票背面形状和大小完全相同）．
（1）若从中随机抽取一张，抽到的是“立夏”的概率是 ；
（2）小明的妹妹想要“立春”和“秋分”，小明让妹妹从中随机抽取一张后（不放回），再从中随机抽取一张，请用列表或画树状图的方法求妹妹抽到的两张邮票恰好是“立春”和“秋分”的概率．（立春、立夏、秋分、大寒可以分别用A，B，C，D表示）
21. 物理实验技能考核前，小亮对“探究凸透镜成像规律”的实验进行了反复练习．在练习的过程中，他惊喜地发规“蜡烛在燃烧过程中，其剩余高度与燃烧时间之间呈一次函数关系”．已知蜡烛燃烧6分钟后，蜡烛剩余高度，蜡烛燃烧20分钟后，蜡烛剩余高度．
（1）求y与t的函数表达式；
（2）小亮晚上7时15分点亮一支新蜡烛，但有一段时间风把蜡烛吹灭了，后又点亮蜡烛，至晚上9时15分蜡烛燃烧了一半，问其间蜡烛熄灭了几分钟？
22. 2024年2月23日，第三届“天宫画展”在中国空间站开展．神舟十七号航天员乘组在轨展示和介绍了新时代青少年畅想中国式现代化美丽画卷，并向全国青少年发出邀请，相约待到中华人民共和国成立100周年时，共同见证几代人为之艰辛求索、牺牲奉献、接续奋斗的现代化中国．
西安市某中学掀起了“航天有我，筑梦太空”的阅读月活动，为了解学生们课外阅读有关航天书籍的情况，随机抽取名学生，对每人每周课外阅读航天书籍的平均时间进行了调查：
【收集数据】，，，，，，，，，，，，，，，，，，，
整理数据】
【分析数据】
请根据以上提供的信息，解答下列问题：
（1）填空： ， ， ；
（2）如果根据表格设计扇形统计图，等级对应的扇形圆心角的度数是多少?
（3）等级为及以上为达标，该校现有学生人，估计达标的学生有多少人?
23. 某数学兴趣小组在综合实践活动中测量古塔的高度．
【测量方案】在地面上选一点，垂直地面竖立标杆，后退2m到处，此时在一直线上；另选一点，垂直地面竖立标杆，后退4m到处，此时三点也在一直线上．
【测量数据】两次测量标杆之间的距离是为50m，两个标杆的高度均为m，且在同一直线上．
请你根据以上测量数据，帮助兴趣小组求出古塔的高度．
24. 如图，为直径，点为圆上一点，是的中点，连接交于点，过作的切线交的延长于点．
（1）求证：；
（2）若，，求的长．
25. 某公园有一个喷泉景观，在一个柱形高台上装有喷水管，水管喷头斜着喷出水柱，经过测量水柱在不同位置到水管的水平距离x米和对应的竖直高度y米，
整理如下：
（1）根据表格数据，在如下坐标系中描点、连线；猜想y与x之间满足我们学过的哪类函数关系，并求y与x之间的函数表达式；
（2）此喷水管可以上下调节，喷出的水柱形状不变且随之上下平移，若调节后的落水点（水落到地面的位置）向左平移了1米，求喷水管需要向下平移多少米?
26 问题提出：
（1）如图①，在中，，，以为边在外作等边，过点作于，连接，求的值；
问题解决：
（2）2024年国际沙滩排球世界锦标赛将在陕西商洛举行，为迎接此次锦标赛，促进全民健身，计划修建一个四边形运动公园如图②所示．运动公园（即四边形）需建在公路的一边，现场测量，根据有关设计要求：运动公园还要满足，，且，那么是否存在面积最大的运动公园?若存在，请求出运动公园面积的最大值；若不存在，请说明理由．课外阅读时间x（min）
等级
人数
平均数
中位数
众数
分钟
分钟
分钟
水平距离x（米）
1
2
3
4
5
竖直距离y（米）
5