浙教版九年级下册2.1 直线和圆的位置关系优秀教学课件ppt

这是一份浙教版九年级下册2.1 直线和圆的位置关系优秀教学课件ppt，文件包含大单元浙教版数学九年级下册212《直线与圆的位置关系》课件pptx、大单元浙教版数学九年级下册212《直线与圆的位置关系》教学设计docx、大单元浙教版数学九年级下册第2章《直线与圆的位置关系》单元教学设计doc等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

1.理解切线的判定定理，并能初步运用它解决简单的问题.2.知道判定切线的常用的三种方法，初步掌握方法的选择.3.掌握在解决切线的问题中常用的辅助线的作法.
下雨天，你快速转动雨伞时，雨水飞出的情景你看见过吗？工人师傅用砂轮打磨工件飞出火星的情景见过吗？
思考下雨点和火星运动的轨迹与转动的“圆” 有怎样的关系？
按照下述步骤作图：如图，在⊙O上任取一点A．连结OA．过点A作直线l⊥OA．思考以下问题（可与你的同伴交流）：（1）圆心O到直线l的距离和圆的半径有什么关系？（2）直线l与⊙O的位置有什么关系？根据什么？（3）由此你发现什么？
解：（1）圆心O到直线l的距离等于圆的半径长．（2）直线l与⊙O相切，根据d＝r直线与⊙O相切．（3）经过半径的外端并且垂直这条半径的直线是圆的切线．
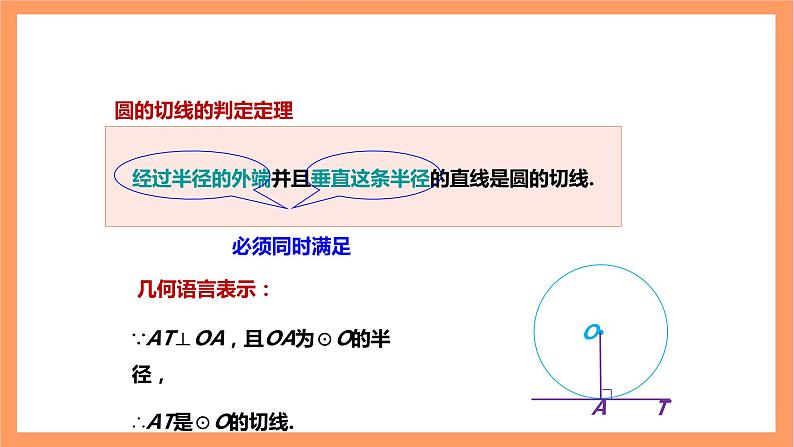
经过半径的外端并且垂直这条半径的直线是圆的切线.
∵AT⊥OA，且OA为⊙O的半径，∴AT是⊙O的切线.
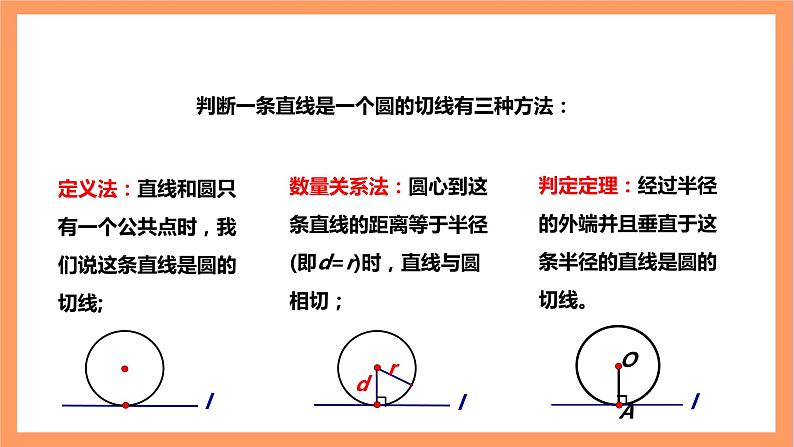
判断一条直线是一个圆的切线有三种方法：
定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;
数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；
判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。
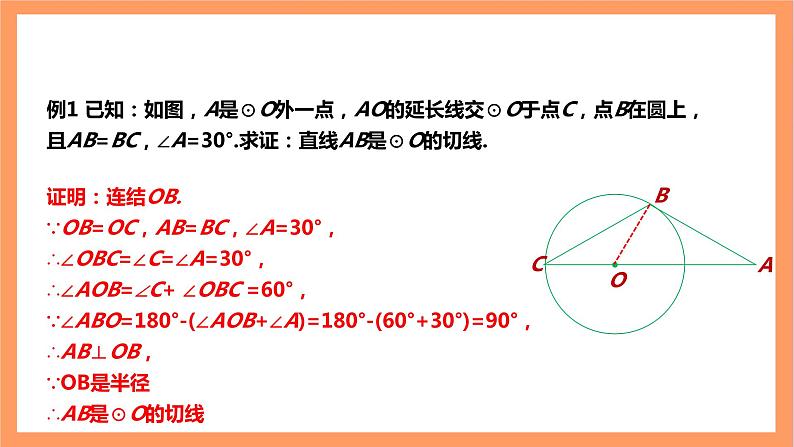
例1 已知：如图，A是⊙O外一点，AO的延长线交⊙O于点C，点B在圆上，且AB=BC，∠A=30°.求证：直线AB是⊙O的切线.
证明：连结OB.∵OB=OC，AB=BC，∠A=30°，∴∠OBC=∠C=∠A=30°，∴∠AOB=∠C+ ∠OBC =60°，∵∠ABO=180°-(∠AOB+∠A)=180°-(60°+30°)=90°，∴AB⊥OB，∵OB是半径∴AB是⊙O的切线
1.有交点，连半径，证垂直
变式1 直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证:直线AB是⊙O的切线.
证明：连接OC，如图，∵ OA=OB，CA=CB，∴OC丄AB，∴直线AB是⊙O的切线
变式2 如图，在Rt△ABC中，∠ACB=90°，AO是△ABC 的角平分线.以O为圆心，OC为半径作⊙O.求证：AB是⊙O的切线.
证明：如图，过点O作OF丄AB于点F，∵ AO 平分 ∠CAB,OC 丄 AC，OF 丄 AB，∴OC=OF,∴AB是⊙O的切线；
2.无交点，作垂线，证半径
(1)如果已知直线经过圆上一点，则连结这点和圆心，得到辅助半径，再证所作半径与这直线垂直. 简记为：连半径，证垂直.(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线，再证垂线长等于半径长.简记为：作垂直，证半径.
例2、如图，台风中心P（100，200）沿北偏东30°的方向移动，受台风影响区域的半径为200km,那么下列城市A（200，380），B（600，480），C（550，300），D（370，540 ）中，哪些受到这次台风的影响，哪些不受到这次台风的影响？
解：如图，在直角坐标系中画出以点P（100,200）为圆心，以200为半径的⊙P，再在点P处画出北偏东30°方向的方向线，作垂直于方向线的⊙P的直径HK，分别过点H，K作⊙O的切线l1，l2，则l1∥l2.又因为台风圈在两条平行线l1，l2之间移动，点A，D落在切线l1，l2之间，所以受到这次台风的影响；而点B，C不在切线l1，l2之间，所以不受到这次台风的影响.
【知识技能类作业】必做题：
1.如图，在平面直角坐标系中，过格点A，B，C画圆弧，则点B与下列格点连线所得的直线中，能够与该圆弧相切的是（　　）A.(5,2)B.(2,4) C.(1,4)D.(6,2)2．如图，△ABC是⊙O的内接三角形，下列选项中，能使过点A的直线EF与⊙O相切于点A的条件是(　　)A．∠EAB＝∠C B．∠B＝90° C．EF⊥AC D．以上答案均可以
3.如图，PA切⊙O于点A，该圆的半径为3，PO=5，则PA的长等于______.
4.如图，A，B是⊙O上的两点，AC是⊙O的切线，∠B＝70°，则∠BAC＝________.
【知识技能类作业】选做题：
5.如图，OP是⊙O的半径，∠POT＝60°，OT交⊙O于点S．（1）过点P作⊙O的切线．（2）过点P的切线交OT于点Q，判断点S是不是线段OQ的中点，并说明理由．
（2）点S是OQ的中点．∵PQ为⊙O的切线，∴∠OPQ＝90°．∵∠POQ＝60°，∴∠OQP＝30°，∴OQ＝2PO．∵PO＝SO，∴OQ＝2SO，即点S是OQ的中点．
6.如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M.求证：CD与⊙O相切．
证明：连接OM，过点O作ON⊥CD于点N，∵⊙O与BC相切于点M，∴OM⊥BC.又∵ON⊥CD，O为正方形ABCD对角线AC上一点，∴OM＝ON，∴CD与⊙O相切．
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法： ①有公共点，连半径，证垂直；②无公共点，作垂直，证半径.
3．如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为_________________________.4．如图，四边形ABCD内接于⊙O，AD∥BC，直线EF是⊙O的切线，B是切点．若∠C＝80°，∠ADB＝54°，则∠CBF＝________.
∠ABC＝90°(或AB⊥BC)　
5．如图，AC是⊙O的直径，AC＝10 cm，PA，PB是⊙O的切线，点A，B为切点．过点A作AD⊥BP于点D，连结AB，BC．(1)求证：△ABC∽△ADB；(2)若切线AP的长为12 cm，求弦AB的长．
(1)证明：连结OB．∵PB是⊙O的切线，∴OB⊥BP.又∵AD⊥BP，∴OB∥AD，∴∠OBA＝∠BAD．∵OB＝OA，∴∠OBA＝∠CAB＝∠BAD．又∵∠CBA＝∠BDA＝90°，∴△ABC∽△ADB．