押新高考第12题 集合-2024年高考数学押题（新高考通用）

这是一份押新高考第12题 集合-2024年高考数学押题（新高考通用），文件包含押新高考第12题集合原卷版docx、押新高考第12题集合解析版docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。


1．（2023·新高考Ⅰ卷高考真题第1题）已知集合，，则（ ）
A．B．C．D．
【答案】C
【分析】方法一：由一元二次不等式的解法求出集合，即可根据交集的运算解出．
方法二：将集合中的元素逐个代入不等式验证，即可解出．
【详解】方法一：因为，而，
所以．
故选：C．
方法二：因为，将代入不等式，只有使不等式成立，所以．
故选：C．
2．（2023·新高考Ⅱ卷高考真题第2题）设集合，，若，则（ ）．
A．2B．1C．D．
【答案】B
【分析】
根据包含关系分和两种情况讨论，运算求解即可.
【详解】因为，则有：
若，解得，此时，，不符合题意；
若，解得，此时，，符合题意；
综上所述：.
故选：B.
3．（2022·新高考Ⅰ卷高考真题第1题）若集合，则（ ）
A．B．C．D．
【答案】D
【分析】求出集合后可求.
【详解】，故，
故选：D
4．（2022·新高考Ⅱ卷高考真题第1题）已知集合，则（ ）
A．B．C．D．
【答案】B
【分析】方法一：求出集合后可求.
【详解】[方法一]：直接法
因为，故，故选：B.
[方法二]：【最优解】代入排除法
代入集合，可得，不满足，排除A、D；
代入集合，可得，不满足，排除C.
故选：B.
【整体分析】方法一：直接解不等式，利用交集运算求出，是通性通法；
方法二：根据选择题特征，利用特殊值代入验证，是该题的最优解．
5．（2021·新高考Ⅰ卷高考真题第1题）设集合，，则（ ）
A．B．C．D．
【答案】B
【分析】利用交集的定义可求.
【详解】由题设有，
故选：B .
6．（2021·新高考Ⅱ卷高考真题第2题）设集合，则（ ）
A．B．C．D．
【答案】B
【分析】根据交集、补集的定义可求.
【详解】由题设可得，故，
故选：B.
集合有个元素，子集有个，真子集有个，非空真子集个数为个.
，
1．（2024·福建漳州·一模）若集合，，则 ．
【答案】
【分析】
根据集合的交集运算求解即可.
【详解】由题意可得：.
故答案为：.
2．（2024·河南·一模）若集合，则 ．
【答案】
【分析】
根据题意结合交集运算求解.
【详解】
由可得．
故答案为：.
3．（2024·安徽池州·二模）已知集合，则 .
【答案】
【分析】求出集合后可得.
【详解】，故.
故答案为：.
4．（2024·山东临沂·一模）集合，，则 .
【答案】
【分析】首先解对数不等式求出集合，再解分式不等式求出集合，最后根据补集、交集的定义计算可得.
【详解】由，可得，则，
所以，
由，可得，等价于，解得，
所以，
所以，所以.
故答案为：
5．（2024·全国·模拟预测）若集合，则集合的真子集的个数为 ．
【答案】3
【分析】根据交集运算求出，然后由n元集合的真子集个数为可得.
【详解】因为，
所以，所以集合的真子集的个数为．
故答案为：3
6．（2024·湖南长沙·一模）已知集合，，则的真子集的个数为 .
【答案】7
【分析】由对数的定义域求得集合A，再由交集的定义及真子集个数与元素个数的关系即可得解.
【详解】由，得，
所以的真子集的个数为.
故答案为：7.
7．（2024·贵州·三模）已知集合，若，则实数的取值范围为 .
【答案】
【分析】
先由得出；再求出集合A，结合集合的包含关系列出不等式组即可求解.
【详解】因为，
所以.
又因为，，
所以，解得：，
所以实数的取值范围为.
故答案为：
8．（2024·山东青岛·一模）已知集合，，则的所有元素之和为 ．
【答案】0
【分析】
求出集合B，再求，然后可得.
【详解】由题知，，
所以，
所以的所有元素之和为.
故答案为：0
9．（2024·全国·模拟预测）已知集合，，则的元素个数是 .
【答案】
【分析】判断方程组解的个数，可得结果.
【详解】联立可得，则，
得原方程组有两组解，即中有个元素.
故答案为：.
10．（2024·湖南·模拟预测）已知全集，集合，则 ．
【答案】
【分析】根据集合的运算即可求解.
【详解】由已知，又，
所以．
故答案为：
11．（2024·山东济宁·一模）设集合，，若，则实数的取值范围是 ．
【答案】
【分析】求解一元二次不等式解得集合，再根据集合的包含关系，列出不等式求解即可.
【详解】集合，
又，且，
故可得，即，解得.
故答案为：.
12．（2024·辽宁·一模）已知集合，，则 ， .
【答案】
【分析】首先解一元二次不等式求出集合，再根据交集的定义计算可得.
【详解】由，即，解得，
所以，
又，所以.
故答案为：；
13．（2024·广东湛江·一模）已知全集为实数集，集合，，则 ．
【答案】
【分析】解不等式可分别求得集合，根据并集和补集定义可得到结果.
【详解】由得：，即；
由得：，即，，.
故答案为：.
14．（2024·辽宁丹东·一模）已知集合，，若，则的取值范围是 ．
【答案】
【分析】由题意可得，则有，即可得解.
【详解】因为，，
所以，
则不等式无解，
所以，解得.
故答案为：.
15．（2024·湖南·二模）已知集合，若集合恰有两个元素，则实数的取值范围是 .
【答案】
【分析】解二次不等式化简集合，再利用二次不等式解的形式与交集的结果即可得解.
【详解】因为，
，
又集合恰有两个元素，
所以恰有两个元素1和2，所以.
故答案为：.
16．（2024·辽宁葫芦岛·一模）已知集合，．若，则实数的取值集合为 ．
【答案】
【分析】
根据，得到集合的元素都是集合的元素，即可求得的值.
【详解】由题意，所以或，则或，
所以实数的取值集合为.
故答案为：.
17．（2024·吉林白山·二模）已知集合，若，则实数的取值范围为 .
【答案】
【分析】
根据题意求集合，根据分析求解.
【详解】由题意可知：，
因为，则，
所以实数的取值范围为.
故答案为：.
18．（2024·安徽合肥·一模）已知集合，若，则的取值范围是 .
【答案】
【分析】
利用一元二次不等式的解法及交集的定义即可求解.
【详解】由，得,解得，
所以.
因为，
所以或，解得或，
所以的取值范围是.
故答案为：.
19．（2024·全国·模拟预测）设集合.若且，则 .
【答案】6
【分析】根据集合间的关系可知，可得，再由求得，即可得解.
【详解】因为集合，
若，则且，可得，解得，
即有，又，所以，所以.
故答案为：6
20．（2024·河南信阳·二模）已知集合，，那么 ．
【答案】
【分析】首先由函数定义域化简集合，求复杂分式、根式函数的值域得集合，结合集合的交集、补集概念即可求解.
【详解】要使得有意义，则，解得，即集合，
若有意义，则，且，
而且，所以且，
所以或，从而，.
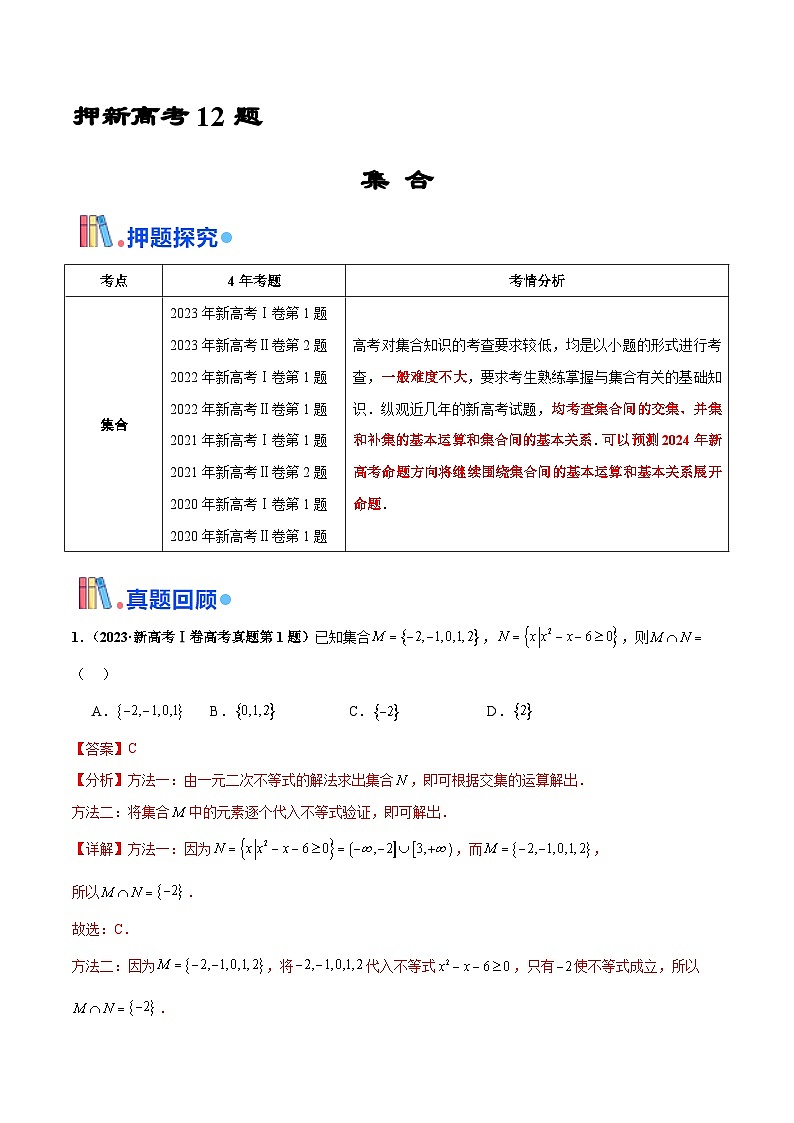
故答案为：.考点
4年考题
考情分析
集合
2023年新高考Ⅰ卷第1题
2023年新高考Ⅱ卷第2题
2022年新高考Ⅰ卷第1题
2022年新高考Ⅱ卷第1题
2021年新高考Ⅰ卷第1题
2021年新高考Ⅱ卷第2题
2020年新高考Ⅰ卷第1题
2020年新高考Ⅱ卷第1题
高考对集合知识的考查要求较低，均是以小题的形式进行考查，一般难度不大，要求考生熟练掌握与集合有关的基础知识．纵观近几年的新高考试题，均考查集合间的交集、并集和补集的基本运算和集合间的基本关系．可以预测2024年新高考命题方向将继续围绕集合间的基本运算和基本关系展开命题．