2024 年湖北省中考数学模拟试卷（解析版）

这是一份2024 年湖北省中考数学模拟试卷（解析版），共20页。
案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2 ．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题（共 10 小题，每小题 3 分，共 30 分）
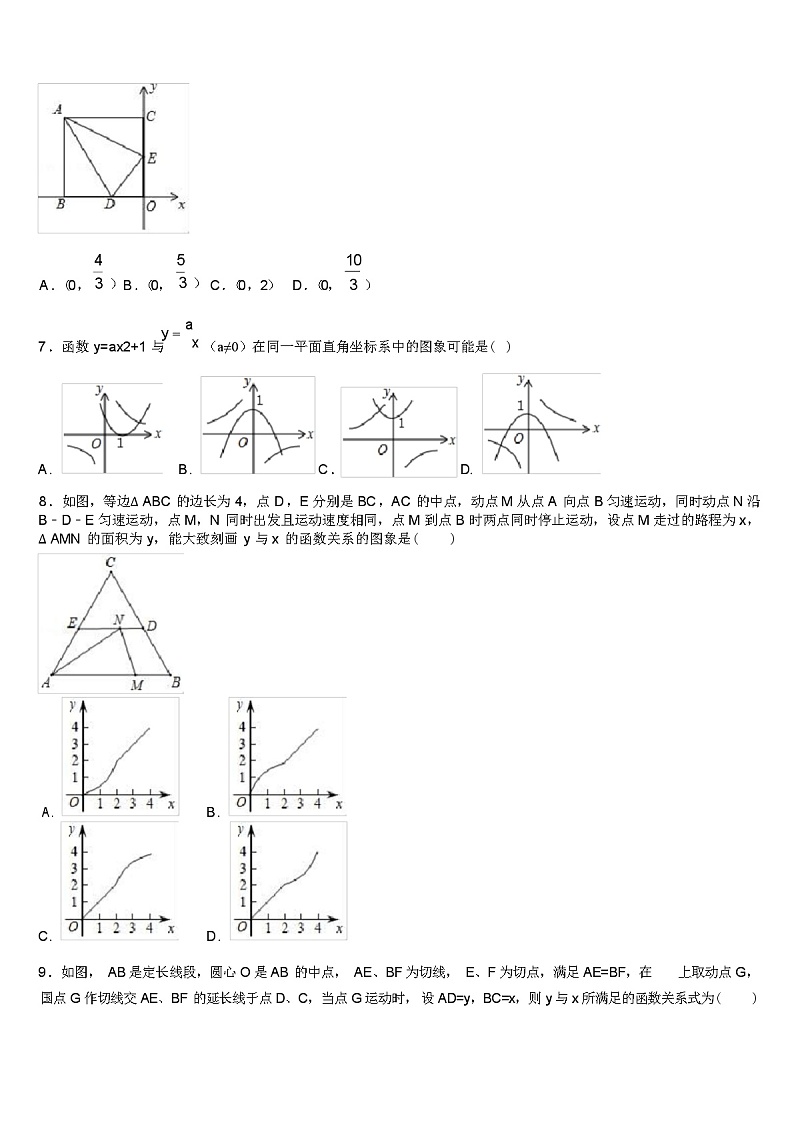
1 ．下列图形中，既是中心对称图形，又是轴对称图形的是( )
A .
B .
C .
D .
2 ．如图 1 是 2019 年 4 月份的日历，现用一长方形在日历表中任意框出 4 个数(如图 2)，下列表示 a，b ，c，d 之间关 系的式子中不正确的是( )
A ．a﹣d ＝b﹣c B ．a+c+2 ＝b+d C ．a+b+14 ＝c+d D ．a+d ＝b+c
3 ．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是( )
A .
B .
C .
D .
4 ．如果 m 的倒数是﹣1 ，那么 m2018 等于( )
A ．1 B . ﹣1 C ．2018 D . ﹣2018
5 ．如图， 有一矩形纸片 ABCD，AB=10，AD=6，将纸片折叠，使 AD 边落在 AB 边上， 折痕为 AE，再将ΔAED 以
DE 为折痕向右折叠，AE 与 BC 交于点 F，则
ΔCEF
的面积为( )
A ．4 B ．6 C ．8 D ．10
6 ．如图， 矩形 ABOC 的顶点 A 的坐标为(﹣4，5），D 是 OB 的中点，E 是 OC 上的一点，当Δ ADE 的周长最小时，
点 E 的坐标是( )
4
A ．（0 ， 3 ）B ．（0，
5
3 ） C ．（0 ，2） D ．（0，
10
3 ）
y = a
7 ．函数 y=ax2+1 与 x （a≠0）在同一平面直角坐标系中的图象可能是( )
A .
B .
C ． D.
8 ．如图，等边Δ ABC 的边长为 4，点 D ，E 分别是 BC ，AC 的中点，动点 M 从点 A 向点 B 匀速运动，同时动点 N 沿 B﹣D﹣E 匀速运动，点 M，N 同时出发且运动速度相同，点 M 到点 B 时两点同时停止运动，设点 M 走过的路程为 x， Δ AMN 的面积为 y，能大致刻画 y 与 x 的函数关系的图象是( )
A .
C .
B .
D .
9 ．如图， AB 是定长线段，圆心 O 是 AB 的中点， AE、BF 为切线， E、F 为切点，满足 AE=BF，在 上取动点 G，
国点 G 作切线交 AE、BF 的延长线于点 D、C，当点 G 运动时， 设 AD=y，BC=x，则 y 与 x 所满足的函数关系式为( )
A ．正比例函数 y=kx（k 为常数， k≠0 ，x＞0）
B ．一次函数 y=kx+b（k，b 为常数， kb≠0 ，x＞0）
k
C ．反比例函数 y= x （k 为常数， k≠0 ，x＞0）
D ．二次函数 y=ax2+bx+c（a，b，c 为常数， a≠0 ，x＞0）
10 ．如图，将Δ ABC 绕点 B 顺时针旋转 60°得Δ DBE，点 C 的对应点 E 恰好落在 AB 延长线上，连接 AD ．下列结论
一定正确的是( )
A . ∠ABD=∠E B . ∠CBE=∠C C ．AD∥BC D ．AD ＝BC
二、填空题（本大题共 6 个小题，每小题 3 分，共 18 分）
11．函数y = x +3 的定义域是 .
12 ．正八边形的中心角为 度.
13 ．如图，线段 AC=n+1（其中 n 为正整数），点 B 在线段 AC 上，在线段 AC 同侧作正方形 ABMN 及正方形 BCEF， 连接 AM、ME、EA 得到Δ AME．当 AB=1 时， Δ AME 的面积记为 S1；当 AB=2 时， Δ AME 的面积记为 S2；当 AB=3
时 ， Δ AME 的 面 积 记 为 S3 ； ⅆ ; 当 AB=n 时 ， Δ AME 的 面 积 记 为 Sn ． 当 n≥2 时 ， Sn ﹣ Sn ﹣ 1=
▲ .
14．在我国著名的数学书《九章算术》中曾记载这样一个数学问题： “今有共买羊，人出五，不足四十五；人出七，不
足三，问人数、羊价各几何？ ”其大意是：今有人合伙买羊，若每人出 5 钱，还差 45 钱；若每人出 7 钱，还差 3 钱， 问合伙人数、羊价各是多少？设羊价为 x 钱， 则可列关于 x 的方程为 .
15 ．将一个底面半径为 2，高为 4 的圆柱形纸筒沿一条母线剪开，所得到的侧面展开图形面积为 .
16 ．如图， AB∥CD ，BE 交 CD 于点 D，CE⊥BE 于点 E，若∠B=34° , 则∠C 的大小为 度.
三、 解答题（共 8 题，共 72 分）
1
+ (2019 一 π )
(
)
2sin60
4x(x + 3) = x2 一 9
1
0
17 ．（8 分）计算：
; 解方程：
- |一一+1一 tan60 2
18
.（8 分）已知，在菱形 ABCD 中，∠ADC=60°,点 H 为 CD 上任意一点（不与 C 、D 重合），过点 H 作 CD 的垂线，
交 BD 于点 E，连接 AE .
（1）如图 1，线段 EH 、CH 、AE 之间的数量关系是 ；
（2）如图 2，将Δ DHE 绕点 D 顺时针旋转，当点 E、H、C 在一条直线上时，求证： AE+EH=CH .
19 ．（8 分）甲、乙两个人做游戏：在一个不透明的口袋中装有 1 张相同的纸牌，它们分别标有数字 1，2 ，3，1 ．从中 随机摸出一张纸牌然后放回， 再随机摸出一张纸牌， 若两次摸出的纸牌上数字之和是 3 的倍数， 则甲胜； 否则乙胜．这
个游戏对双方公平吗？请列表格或画树状图说明理由.
C
20 ．（8 分）在Δ ABC 中， AB=AC，∠BAC=α,点 P 是Δ ABC 内一点，且∠PAC+∠PCA=2 ，连接 PB，试探究 PA、
PB 、PC 满足的等量关系.
（1）当 α=60°时，将Δ ABP 绕点 A 逆时针旋转 60°得到Δ ACP′，连接 PP′，如图 1 所示．由Δ ABP≌△ACP′可以证得
Δ APP′是等边三角形，再由∠PAC+∠PCA=30°可得∠APC 的大小为 度，进而得到Δ CPP′是直角三角形，这样
可以得到 PA、PB 、PC 满足的等量关系为 ；
（2）如图 2，当 α=120°时， 参考（1）中的方法，探究 PA 、PB、PC 满足的等量关系， 并给出证明；
（3）PA、PB 、PC 满足的等量关系为 .
21 ．（8 分） “端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉 馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用 A 、B 、C、D 表示)这四种不同口味粽子的喜爱情况，在节前对某 居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图(尚不完整) .
请根据以上信息回答：
(1)本次参加抽样调查的居民有多少人？
(2)将两幅不完整的图补充完整；
(3)求扇形统计图中 C 所对圆心角的度数；
(4)若有外型完全相同的 A、B 、C 、D 粽各一个， 煮熟后， 小王吃了两个．用列表或画树状图的方法，求他第二个吃到 的恰好是 C 粽的概率.
( x2 1 1 ) 1
22 ．（10 分）先化简，再求值： x2 2x +1 x x 1 ，其中 x=﹣1 .
23 ．（12 分） “低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，
绘制了如下统计图：
（1）填空：样本中的总人数为 ；开私家车的人数 m= ；扇形统计图中“骑自行车”所在扇形的圆心角为
度；
（2）补全条形统计图；
（3）该单位共有 2000 人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车．若步行，坐公交 车上下班的人数保持不变，问原来开私家车的人中至少有多少人改为骑自行车，才能使骑自行车的人数不低于开私家
车的人数？
24 ．如图 1，抛物线 y=ax2+bx﹣2 与 x 轴交于点 A(﹣1，0），B（4 ，0）两点，与 y 轴交于点 C，经过点 B 的直线交 y 轴于点 E（0 ，2）.
（1）求该抛物线的解析式；
（2）如图 2，过点 A 作 BE 的平行线交抛物线于另一点 D，点 P 是抛物线上位于线段 AD 下方的一个动点， 连结 PA，
EA，ED，PD，求四边形 EAPD 面积的最大值；
（3）如图 3，连结 AC，将Δ AOC 绕点 O 逆时针方向旋转，记旋转中的三角形为Δ A′OC′，在旋转过程中，直线 OC′
与直线 BE 交于点 Q，若Δ BOQ 为等腰三角形， 请直接写出点 Q 的坐标.
参考答案
一、选择题 （共 10 小题，每小题 3 分，共 30 分）
1 、C
【解析】
根据中心对称图形和轴对称图形对各选项分析判断即可得解.
【详解】
A 、不是轴对称图形，是中心对称图形， 故本选项错误；
B 、不是中心对称图形，是轴对称图形， 故本选项错误；
C、既是中心对称图形，又是轴对称图形，故本选项正确；
D、是轴对称图形，不是中心对称图形，故本选项错误.
故选 C .
【点睛】
本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对
称图形是要寻找对称中心，旋转 180 度后两部分重合.
2 、A
【解析】
观察日历中的数据，用含 a 的代数式表示出 b，c，d 的值，再将其逐一代入四个选项中，即可得出结论. 【详解】
解：依题意，得： b ＝a+1，c ＝a+7，d ＝a+1 .
A、∵ a﹣d ＝a﹣(a+1) =﹣ 1 ，b﹣c ＝a+1﹣(a+7) =﹣ 6，
∴a﹣d≠b﹣c，选项 A 符合题意；
B、∵a+c+2 ＝a+(a+7)+2 ＝2a+9，b+d ＝a+1+(a+1) ＝2a+9，
∴a+c+2 ＝b+d，选项 B 不符合题意；
C、∵a+b+14 ＝a+(a+1)+14 ＝2a+15，c+d ＝a+7+(a+1) ＝2a+15，
∴a+b+14 ＝c+d，选项 C 不符合题意；
D、∵a+d ＝a+(a+1) ＝2a+1，b+c ＝a+1+(a+7) ＝2a+1，
∴a+d ＝b+c，选项 D 不符合题意.
故选： A .
【点睛】
考查了列代数式，利用含 a 的代数式表示出 b，c，d 是解题的关键.
3 、D
【解析】
A ，B ，C 只能通过旋转得到， D 既可经过平移，又可经过旋转得到，故选 D.
4 、A
【解析】
因为两个数相乘之积为 1,则这两个数互为倒数, 如果 m 的倒数是﹣1,则 m=-1,
然后再代入 m2018 计算即可.
【详解】
因为 m 的倒数是﹣1,
所以 m=-1,
所以 m2018=（-1）2018=1,故选 A.
【点睛】
本题主要考查倒数的概念和乘方运算,解决本题的关键是要熟练掌握倒数的概念和乘方运算法则.
5 、C
【解析】
1
根据折叠易得 BD ，AB 长，利用相似可得 BF 长，也就求得了 CF 的长度， Δ CEF 的面积= 2 CF•CE .
【详解】
解： 由折叠的性质知，第二个图中 BD=AB-AD=4 ，第三个图中 AB=AD-BD=2，
因为 BC∥DE，
所以 BF：DE=AB：AD，
所以 BF=2 ，CF=BC-BF=4，
1
所以Δ CEF 的面积=
2
CF•CE=8；
故选： C .
点睛：
本题利用了：①折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小
不变，位置变化，对应边和对应角相等；②矩形的性质，平行线的性质，三角形的面积公式等知识点.
6 、B
【解析】
解：作 A 关于 y 轴的对称点 A′，连接 A′D 交 y 轴于 E，则此时，Δ ADE 的周长最小. ∵四边形 ABOC 是矩形，∴AC∥OB， AC=OB . ∵A 的坐标为(﹣4 ，5），∴A′（4 ，5），B(﹣4，0）.
∵D 是 OB 的中点，∴D(﹣2 ，0）.
5
(
6
5
〈
|k =
( 5 = 4k + b 〈
设直线 DA′的解析式为 y=kx+b，∴l0 = -2k + b ，∴
5 5 5
y = x + - - ,∴直线 DA′的解析式为 6 3 ．当 x=0 时， y= 3 ，
3
b =
5
∴E（0 ， 3 ）．故选 B .
7 、B
【解析】
试题分析：分 a＞0 和 a＜0 两种情况讨论：
a
y = -
当 a＞0 时， y=ax2+1 开口向上，顶点坐标为（0 ，1）； x 位于第一、三象限，没有选项图象符合；
a
y = -
当 a＜0 时， y=ax2+1 开口向下，顶点坐标为（0 ，1）； x 位于第二、四象限， B 选项图象符合.
故选 B .
考点： 1.二次函数和反比例函数的图象和性质； 2.分类思想的应用.
8 、A
【解析】
根据题意， 将运动过程分成两段．分段讨论求出解析式即可.
【详解】
∵BD=2 ， ∠B=60° ,
∴点 D 到 AB 距离为 3 ，
当 0≤x≤2 时，
x x＝ x2
y= 2 2 4 ；
1 • 3 3
1
当 2≤x≤4 时， y= 2
x • 3=
3
x 2
.
根据函数解析式， A 符合条件.
故选 A .
【点睛】
本题为动点问题的函数图象，解答关键是找到动点到达临界点前后的一般图形，分类讨论，求出函数关系式.
9 、C
【解析】
延长 AD，BC 交于点 Q，连接 OE，OF，OD，OC，OQ，由 AE 与 BF 为圆的切线，利用切线的性质得到 AE 与 EO 垂 直， BF 与 OF 垂直，由 AE=BF，OE=OF，利用 HL 得到直角三角形 AOE 与直角 BOF 全等，利用全等三角形的对应角 相等得到∠A=∠B，利用等角对等边可得出三角形 QAB 为等腰三角形，由 O 为底边 AB 的中点，利用三线合一得到 QO 垂直于 AB，得到一对直角相等，再由∠FQO 与∠OQB 为公共角，利用两对对应角相等的两三角形相似得到三角 形 FQO 与三角形 OQB 相似，同理得到三角形 EQO 与三角形 OAQ 相似，由相似三角形的对应角相等得到 ∠QOE=∠QOF=∠A=∠B，再由切线长定理得到 OD 与 OC 分别为∠EOG 与∠FOG 的平分线，得到∠DOC 为∠EOF 的一半，即∠DOC=∠A=∠B，又∠GCO=∠FCO，得到三角形 DOC 与三角形 OBC 相似，同理三角形 DOC 与三角形 DAO 相似，进而确定出三角形 OBC 与三角形 DAO 相似，由相似得比例，将 AD=x ，BC=y 代入，并将 AO 与 OB 换 为 AB 的一半，可得出 x 与 y 的乘积为定值，即 y 与 x 成反比例函数，即可得到正确的选项.
【详解】
延长 AD ，BC 交于点 Q，连接 OE，OF，OD，OC，OQ，
∵AE ，BF 为圆 O 的切线，
∴OE⊥AE ，OF⊥FB，
∴∠AEO=∠BFO=90° ,
在 RtΔ AEO 和 RtΔ BFO 中，
AE＝BF
{
OE = OF
∵ ,
∴RtΔ AEO≌RtΔ BFO（HL），
∴∠A=∠B，
∴△QAB 为等腰三角形，
又∵O 为 AB 的中点，即 AO=BO，
∴QO⊥AB，
∴∠QOB=∠QFO=90° ,
又∵∠OQF=∠BQO，
∴△QOF∽△QBO，
∴∠B=∠QOF，
同理可以得到∠A=∠QOE，
∴∠QOF=∠QOE，
根据切线长定理得： OD 平分∠EOG，OC 平分∠GOF，
1
________
∴∠DOC= 2 ∠EOF=∠A=∠B，
又∵∠GCO=∠FCO，
∴△DOC∽△OBC，
同理可以得到Δ DOC∽△DAO，
∴△DAO∽△OBC，
∴
AD AO
=
OB BC
,
∴AD•BC=AO•OB=
1 1
4 AB2，即 xy=4 AB2 为定值，
1 k
设 k=4 AB2，得到 y= x ，
k
________
则 y 与 x 满足的函数关系式为反比例函数 y= x （k 为常数， k≠0 ，x＞0）.
故选 C .
【点睛】
本题属于圆的综合题，涉及的知识有：相似三角形的判定与性质，切线长定理，直角三角形全等的判定与性质，反比
例函数的性质，以及等腰三角形的性质，做此题是注意灵活运用所学知识.
10 、C
【解析】
根据旋转的性质得，∠ABD=∠CBE=60°, ∠E=∠C,
则 Δ ABD 为 等 边 三 角 形 ， 即 AD ＝AB=BD, 得 ∠ADB=60° 因 为 ∠ABD = ∠CBE=60° , 则 ∠CBD=60°, 所 以，
∠ADB=∠CBD，得 AD∥BC.故选 C.
二、填空题（本大题共 6 个小题，每小题 3 分，共 18 分）
11 、x≥-1
【解析】
分析：根据二次根式的性质，被开方数大于或等于 0，可以求出 x 的范围.
详解：根据题意得： x+1≥0，解得： x≥﹣1 .
故答案为 x≥﹣1 .
点睛：考查了函数的定义域，函数的定义域一般从三个方面考虑：
（1）当函数表达式是整式时，定义域可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为 0；
（1）当函数表达式是二次根式时，被开方数非负.
12 、45°
【解析】
360。
运用正 n 边形的中心角的计算公式
【详解】
n 计算即可.
360。
= 45。
8
,
解：由正 n 边形的中心角的计算公式可得其中心角为
故答案为 45° .
【点睛】
本题考查了正 n 边形中心角的计算.
13、
2n 一 1
2
【解析】
连接 BE，
∵在线段 AC 同侧作正方形 ABMN 及正方形 BCEF，
∴BE∥AM . ∴△AME 与Δ AMB 同底等高.
∴△AME 的面积= Δ AMB 的面积.
S =
∴当 AB=n 时， Δ AME 的面积为
n
1 n2 S = 1 (n 一 1)2 2 ，当 AB=n－1 时， Δ AME 的面积为 n 2 .
∴当 n≥2 时，
x 一 45
=
14、
5
【解析】
S 一 S
n n 一1
x 一 3
7
1
= n2 一
2
1 (n 一 1)2 = 1 (n+n 一 1)(n 一 n+1)= 2 2
2n 一 1
2
设羊价为 x 钱，根据题意可得合伙的人数为
x 一 45
或
5
x 一 3
7
,由合伙人数不变可得方程.
【详解】
设羊价为 x 钱，
根据题意可得方程：
x 一 45
x 一 45 x 一 3
5 = 7
,
x 一 3
= _______________
故答案为： 5 7 .
【点睛】
本题考查由实际问题抽象出一元一次方程，解答本题的关键是明确题意，列出相应的方程.
15、
【解析】
试题分析：先根据勾股定理求得圆锥的母线长，再根据圆锥的侧面积公式求解即可.
由题意得圆锥的母线长=不=25
则所得到的侧面展开图形面积 .
考点：勾股定理，圆锥的侧面积公式
点评：解题的关键是熟记圆锥的侧面积公式：圆锥的侧面积 底面半径 母线.
16 、56
【解析】
解：∵AB∥CD,
经B = 34，
∴经CDE = 经B = 34，
又∵CE⊥BE，
∴RtΔ CDE 中,
故答案为 56.
经C = 90 - 34 = 56 ，
三、解答题（共 8 题，共 72 分）
x
1
17 、（1）2 （2）
= -3, x = - 1 2
【解析】
（1）原式第一项利用负指数幂法则计算，第二项利用特殊角的三角函数值化简，第三项利用绝对值的代数意义化简， 最后一项利用零指数幂法则计算可得到结果；（2）移项后分解因式，即可得出两个一元一次方程，求出方程的解即可.
【详解】
（1）原式= 2 - 3 + 3 - 1+1=2；
（2）
4x(x + 3) = x2 - 9
4x(x + 3) = (x + 3)(x - 3)
( )
3x + 3 (x + 3) = 0
x ∴ 1
= -3, x = - 1 2
【点睛】
本题考查了实数运算以及平方根的应用，正确掌握相关运算法则是解题的关键.
18 、 (1) EH2+CH2=AE2；(2)见解析.
【解析】
分析：（1）如图 1，过 E 作 EM⊥AD 于 M，由四边形 ABCD 是菱形，得到 AD=CD，∠ADE=∠CDE，通过Δ DME≌△DHE，
根据全等三角形的性质得到 EM=EH，DM=DH，等量代换得到 AM=CH，根据勾股定理即可得到结论；
（2）如图 2，根据菱形的性质得到∠BDC=∠BDA=30° , DA=DC，在 CH 上截取 HG，使 HG=EH，推出Δ DEG 是等
边三角形，由等边三角形的性质得到∠EDG=60°,推出Δ DAE≌△DCG，根据全等三角形的性质即可得到结论.
详解：
（1）EH2+CH2=AE2，
如图 1，过 E 作 EM⊥AD 于 M，
∵四边形 ABCD 是菱形，
∴AD=CD，∠ADE=∠CDE，
∵EH⊥CD，
∴∠DME=∠DHE=90° ,
在Δ DME 与Δ DHE 中，
(|经DME＝经DHE
〈经MDE＝经HDE
|lDE＝DE
,
∴△DME≌△DHE，
∴EM=EH，DM=DH，
∴AM=CH，
在 RtΔ AME 中， AE2=AM2+EM2，
∴AE2=EH2+CH2；
故答案为： EH2+CH2=AE2；
（2）如图 2，
∵菱形 ABCD，∠ADC=60° ,
∴∠BDC=∠BDA=30° , DA=DC，
∵EH⊥CD，
∴∠DEH=60° ,
在 CH 上截取 HG，使 HG=EH，
∵DH⊥EG，∴ED=DG，
又∵∠DEG=60° ,
∴△DEG 是等边三角形，
∴∠EDG=60° ,
∵∠EDG=∠ADC=60° ,
∴∠EDG﹣∠ADG=∠ADC﹣∠ADG，
∴∠ADE=∠CDG，
在Δ DAE 与Δ DCG 中，
(|DA＝DC
〈|lEQ \* jc3 \* hps36 \\al(\s\up 11(经A),DE)EQ \* jc3 \* hps36 \\al(\s\up 11(E＝),DG)经CDG
,
∴△DAE≌△DCG，
∴AE=GC，
∵CH=CG+GH，
∴CH=AE+EH .
点睛：考查了全等三角形的判定和性质、菱形的性质、旋转的性质、等边三角形的判定和性质，解题的关键是正确的
作出辅助线.
19、不公平
【解析】
【分析】列表得到所有情况，然后找出数字之和是 3 的倍数的情况，利用概率公式计算后进行判断即可得.
【详解】根据题意列表如下：
1
2
3
1
1
（1 ，1）
（2 ，1）
（3 ，1）
（1，1）
2
（1 ，2）
（2 ，2）
（3 ，2）
（1，2）
3
（1 ，3）
（2 ，3）
（3 ，3）
（1，3）
1
（1 ，1）
（2 ，1）
（3 ，1）
（1，1）
所有等可能的情况数有 16 种，其中两次摸出的纸牌上数字之和是 3 的倍数的情况有： （2，1），（1，2），（1 ，2），（3，
3），（2，1），共 5 种，
5
∴P （甲获胜） = 16 ，P （乙获胜） =1﹣
5
16
=
11
16
,
则该游戏不公平.
【点睛】本题考查了列表法或树状图法求概率，判断游戏的公平性，用到的知识点为：概率=所求情况数与总情况数之
比.
4PA2 sin 2 C +PC2 = PB2
20 、（1）150， PA2 +PC 2 = PB 2 （1）证明见解析（3） 2
【解析】
（1）根据旋转变换的性质得到Δ PAP′为等边三角形，得到∠P′PC ＝90°,根据勾股定理解答即可；
（1）如图 1，作将Δ ABP 绕点 A 逆时针旋转 110°得到Δ ACP′ ，连接 PP′，作 AD⊥PP′于 D，根据余弦的定义得到 PP′
= 3 PA，根据勾股定理解答即可；
（3）与（1）类似，根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可.
试题解析：
【详解】
解：（1） ∵△ABP≌△ACP′，
∴AP ＝AP′，
由旋转变换的性质可知，∠PAP′ ＝60° , P′C ＝PB，
∴△PAP′为等边三角形，
∴∠APP′ ＝60° ,
1
________
∵∠PAC+∠PCA ＝ 2 ×60° =30° ,
∴∠APC ＝150° ,
∴∠P′PC ＝90° ,
∴PP′1＋PC1 ＝P′C1，
∴PA1＋PC1 ＝PB1，
故答案为 150，PA1＋PC1 ＝PB1；
∵ 即 ∴
（1）如图，作PAP＝120 °,使AP＝AP ，连接PP ， CP ．过点 A 作 AD⊥PP 于 D 点.
BAC＝PAP＝120 ° ,
BAP＋PAC＝PAC＋CAP
,
BAP＝CAP .
∵AB ＝AC，
∴ BAP≌
AP＝AP
,
CAP
.
∴ PC＝PB ，
∵AD⊥PP ，
180。一 PAP
APD＝APD＝＝30
2 ° .
∴ ADP＝90 ° .
∴在 Rt△APD 中，
PD＝AP . csAPD=
3
─ AP
2
.
∴
∵
∴
∴
PP＝2PD＝ 3AP
.
PAC＋PCA＝60 ° ,
APC＝180 一 PAC 一 PCA＝120 ° .
PPC＝APC 一APD＝90 ° .
∴在Rt PPC 中， PP2＋PC 2 ＝PC2 .
∴3PA2＋PC 2 ＝PB 2 ；
（3）如图 1，与（1）的方法类似，
作将Δ ABP 绕点 A 逆时针旋转 α 得到Δ ACP′，连接 PP′，
作 AD⊥PP′于 D，
由旋转变换的性质可知，∠PAP′ = α , P′C ＝PB，
a
∴∠APP′ ＝90° -2
∵∠PAC+∠PCA =
,
a
2
,
a
a
∴∠APC ＝180° -2 ，
a
∴∠P′PC＝（180°-2 ）－（90°-2 ）＝90° ,
∴PP′1＋PC1 ＝P′C1，
a
∵∠APP′ ＝90° -2 ，
a a
∴PD ＝PA•cs（90°-2 ）＝PA•sin 2 ，
a
∴PP′ ＝1PA•sin 2 ，
a
∴4PA1sin1 2 ＋PC1 ＝PB1，
a
故答案为 4PA1sin1 2 ＋PC1 ＝PB1 .
【点睛】
本题考查的是旋转变换的性质、等边三角形的性质、勾股定理的应用，掌握等边三角形的性质、旋转变换的性质、灵
活运用类比思想是解题的关键.
1
________
21 、（1）本次参加抽样调查的居民有 600 人；（2）补图见解析； （3）72°; （4） 4 .
【解析】
试题分析： （1）用 B 的频数除以 B 所占的百分比即可求得结论；
（2）分别求得 C 的频数及其所占的百分比即可补全统计图；
（3）算出 A 的所占的百分比,再进一步算出 C 所占的百分比，再扇形统计图中 C 所对圆心角的度数；
（4）列出树形图即可求得结论.
试题解析： （1）60÷10%=600（人）.
答：本次参加抽样调查的居民有 600 人.
（3）
180
600
x100% = 30%
, 360°×（1－10%－30%－40%）=72° .
（4）如图；
（列表方法略，参照给分）.
3 1
— = -
P（C 粽） = 12 4 .
1
答：他第二个吃到的恰好是 C 粽的概率是4 .
考点： 1 ．条形统计图； 2 ．用样本估计总体； 3 ．扇形统计图； 4 ．列表法与树状图法.
22 、-2.
【解析】
根据分式的运算法化解即可求出答案.
【详解】
( x +1 一 1 ) ?(x 一 1) = x2 +1
解：原式= x 一 1 x x ，
= 一2
(一1)2 +1
当 x=﹣1 时，原式= 一1 .
【点睛】
熟练运用分式的运算法则.
23 、（1）80 ，20，72；（2）16，补图见解析； （3）原来开私家车的人中至少有 50 人改为骑自行车，才能使骑自行车的
人数不低于开私家车的人数.
【解析】
试题分析： （1）用乘公交车的人数除以所占的百分比，计算即可求出总人数，再用总人数乘以开私家车的所占的百分 比求出 m，用 360°乘以骑自行车的所占的百分比计算即可得解：
样本中的总人数为： 36÷45%=80 人；
开私家车的人数 m=80×25%=20；
扇形统计图中“骑自行车”的圆心角为 .
（2）求出骑自行车的人数，然后补全统计图即可.
（3）设原来开私家车的人中有 x 人改为骑自行车，表示出改后骑自行车的人数和开私家车的人数，列式不等式，求解 即可.
试题解析：解： （1）80 ，20 ，72.
（2）骑自行车的人数为： 80×20%=16 人，
补全统计图如图所示；
（3）设原来开私家车的人中有 x 人改为骑自行车，
由题意得， ，解得 x≥50.
答：原来开私家车的人中至少有 50 人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数.
考点： 1.条形统计图； 2.扇形统计图； 3.频数、频率和总量的关系； 4.一元一次不等式的应用.
4 5
﹣ 5 ）.
1 3 12 16 8 5 4 5 8 5
, ,
24、（1）y=2 x2﹣2 x﹣2；（2）9；（3）Q 坐标为(﹣ 5 5 ）或（4﹣ 5 5 ）或（2，1）或（4+ 5 ，
【解析】
试题分析： (1)把点A(-1，0)，B (4，0)代入抛物线 y = ax2 + bx - 2 ，求出 a, b 的值即可.
(2)
先 用 待 定 系 数 法 求 出 直 线 BE 的 解 析 式 ， 进 而 求 得 直 线 AD 的 解 析 式 ， 设
( 1 1 )
G |（m, - 2 m - 2 )|，则
P (|（m, EQ \* jc3 \* hps35 \\al(\s\up 13(1),2) m2
3 )
PG
- 2 m - 2)|，表示出
,用配方法求出它的最大值，
(
1 3
|y =
〈
- x2 - x - 2
2 2
|y =
1
1 1
-2 收 PG 收xD - xA
|l
S
- x - ，
求出点D 的坐标，
联立方程
最大值=
2 2
,
ADP
进而计算四边形 EAPD 面积的最大值；
(3)
分两种情况进行讨论即可.
试题解析： （1）∵ A(-1，0)，B (4，0)在抛物线 y = ax2 + bx - 2 上，
(a -b - 2 = 0
〈
∴l16a + 4b - 2 = 0,
由 ∴
(
∴抛物线的解析式为
x - 2.
1 3
y = x2 -
2 2
解得
|b =
|l
(
〈
|a =
1
2
3
2
（2）过点 P 作PG 」x 轴交 AD 于点 G，
B (4，0)，E (0，2)，
∵
∴直线 BE 的解析式为
x + 2，
1
y = -
2
∵AD∥BE，设直线 AD 的解析式为
1
y = - 2 x + b，
代入
,可得 2
A(-1，0) b = - 1，
∴直线 AD 的解析式为
1 1
y = - x - ，
2 2
设
( 1 1 ) (
G |（m, - 2 m - 2 )|，则 P |（m,
1
-m2 2
3 )
- 2 m - 2)|，
则
PG = |
(
- EQ \* jc3 \* hps35 \\al(\s\up 13(1),2) m - EQ \* jc3 \* hps35 \\al(\s\up 13(1),2) - (|（ EQ \* jc3 \* hps35 \\al(\s\up 13(1),2) m2
3 )
- 2 m - 2)| =
- 1 (m - 1)2 + 2， 2
∴当 x=1 时， PG 的值最大，最大值为 2，
(
1 3
|y =
〈
-x2 - x - 2
2 2
(x = 3
(x = -1
|y =
〈
〈
|l
D (3,
1 1
- x - -，
ly = -2.
解得ly = 0,
或
2 2
-2)，
1
xPGx
=
S
x 一 x
2
∴
最大值=
D A
ADP
∵AD∥BE，
∴S 四边形 APDE 最大=SΔ ADP 最大+
1
x 2 x 4 = 4，
2
S = 4 + 5 = 9.
ADB
S
ADB
1
=
2
x 5 x 2 = 5，
∴
S = S
ADE ADB
= 5，
（3）①如图 3﹣1 中，当
OQ = OB
时，作
OT 」BE
于T.
∵ OB = 4，OE = 2，
OE . OB 8 4 5
OT =
= = ， BE 2 5 5
BE = 2 5，
∴
8 5
,
5
BT = TQ =
∴
16 5
BQ = ，
∴ 5
可得
Q (|（一 1EQ \* jc3 \* hps35 \\al(\s\up 12(2),5) , 1EQ \* jc3 \* hps35 \\al(\s\up 12(6),5)；
(
|4 一
8 5
____________ ，
5
4 5 )
Q
(
1
BO = BQ
②如图 3﹣2 中，当
时,
1
5 )|| .
OQ = BQ
当 2 2
时，
( )
Q2 2，1 ，
当
BO = BQ
3
时， Q3
(
(
|4 +
8 5 4 5 )
5 , 一 5 )|| .
综上所述，满足条件点点 Q 坐标为(|（- 1EQ \* jc3 \* hps35 \\al(\s\up 16(2),5) , 1EQ \* jc3 \* hps35 \\al(\s\up 16(6),5) 或(||（4 - 855 ，455 或 (2，1)或(||（4 + 855 , - 455 .