2024年中考数学精选压轴题之折叠问题

这是一份2024年中考数学精选压轴题之折叠问题，共18页。试卷主要包含了选择题，填空题，解答题，实践探究题等内容，欢迎下载使用。
一、选择题（每题3分，共36分）
1．数学课上，老师让同学们以“矩形的折叠”为主题开展数学活动．如图，小明把矩形ABCD沿DE折叠，使点C落在AB边的点F处，其中DE=55，且sin∠DFA=45，则矩形ABCD的面积为（ ）
A．80B．64C．36D．18
2．如图，已知长方形纸片 ABCD，点E，F分别在边AD和BC上，且∠EFC=53°，H和G 分别是边AD和 BC 上的动点，现将点 A，B 沿 EF 向下折叠至点N，M 处，将点 C，D沿GH 向上折叠至点P，K 处，若 MN∥PK，则∠KHD的度数为 （ ）
A．37°或143°B．74°或96°C．37°或105°D．74°或106°
3．如图，已知BD是矩形ABCD的对角线，AB＝6，BC＝8，点E，F分别在边AD，BC上，连结BE，DF.将△ABE沿BE翻折，将△DCF沿DF翻折，若翻折后，点A，C分别落在对角线BD上的点G，H处，连结GF.则下列结论不正确的是（ ）
A．BD＝10B．HG＝2C．EG∥FHD．GF⊥BC
4．如图，将矩形ABCD沿GE，EC，GF翻折，使得点A，B，D恰好都落在点O处，且点G，O，C在同一条直线上，同时点E，O，F在另一条直线上，小炜同学得出以下结论：①GF∥EC；②AB=435AD；③GE=6DF，④OC=22OF，⑤△COF∽△CEG.其中正确的是（ ）
A．①②③B．①③④C．①④⑤D．②③④
5．如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在边AD，BC上，将纸片ABCD沿直线EF折叠，点C落在边AD上的点H处，点D落在点G处，有下列四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF长的取值范围是3≤BF≤4；④当点H与点A重合时，EF= 25，其中，正确的是（ ）
A．①②③B．①②④C．①③④D．②③④
6．如图，将正方形纸片ABCD沿PQ折叠，使点C的对称点E落在边AB上，点D的对称点为点F，EF为交AD于点G，连接CG交PQ于点H，连接CE．下列四个结论中：①△PBE∽△QFG；②S△CEG＝S△CBE+S四边形CDQH；③EC平分∠BEG；④EG2﹣CH2＝GQ•GD，正确的是（ ）
A．①③B．①③④C．①④D．①②③④
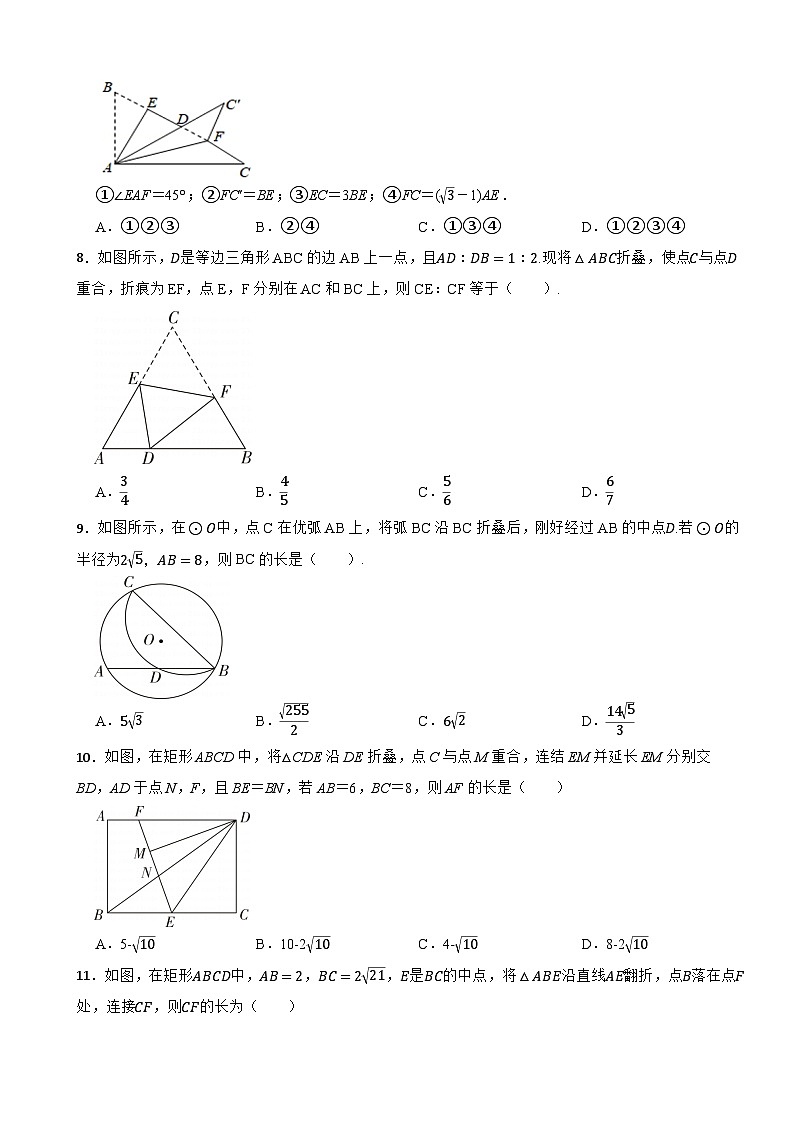
7．如图，在Rt△ABC中，∠BAC＝90°，∠C＝30°，将边AB沿着AE翻折，使点B落在BC上的点D处，再将边AC沿着AF翻折，使得C落在AD延长线上的点C′处，两条折痕与斜边BC分别交于E，F．以下四个结论正确的是（ ）
①∠EAF＝45°；②FC′＝BE；③EC＝3BE；④FC＝(3－1)AE．
A．①②③B．②④C．①③④D．①②③④
8．如图所示，D是等边三角形ABC的边AB上一点，且AD：DB=1：2.现将△ABC折叠，使点C与点D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF等于（ ）.
A．34B．45C．56D．67
9．如图所示，在⊙O中，点C在优弧AB上，将弧BC沿BC折叠后，刚好经过AB的中点D.若⊙O的半径为25，AB=8，则BC的长是（ ）.
A．53B．2552C．62D．1453
10．如图，在矩形ABCD中，将△CDE沿DE折叠，点C与点M重合，连结EM并延长EM分别交BD，AD于点N，F，且BE＝BN，若AB＝6，BC＝8，则AF的长是（ ）
A．5-10B．10-210C．4-10D．8-210
11．如图，在矩形ABCD中，AB=2，BC=221，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连接CF，则CF的长为（ ）
A．8B．425C．172D．9215
12．如图，在菱形纸片ABCD中，∠A＝60°，将纸片折叠，点A，D分别落在点A'，D'处，且A'D'经过点B，EF为折痕，当D'F⊥CD时，CFDF的值为（ ）
A．3−12B．36C．23−16D．3+18
二、填空题（每题3分，共18分）
13． 如图，在矩形ABCD中，E是AD的中点，连接BE，将△ABE沿着BE翻折得到△FBE，EF交BC于点H，延长BF，DC相交于点G，若DG=8，BC=12，则EH= ．
14．如图是一张菱形纸片，∠DAB=60°，AB=5，点E在边AD上，且DE=2，点F在AB边上，把△AEF沿直线EF对折，点A的对应点为点A′，当点A′落在菱形对角线上时，则AF= 。
15．如图，在▱ABCD中，点E在边BC上，将△ABE沿着直线AE翻折得到△AFE，点B的对应点F恰好落在线段DE上，线段AF的延长线交边CD于点G，如果BE：EC＝3：2，那么AF：FG的值等于 ．
16．如图，在扇形AOB中，点C，D在AB上，将D沿弦CD折叠后恰好与OA，OB相切于点E，F.已知∠AOB=120°，OA=6，则EF的度数为 ，折痕CD的长为 .
17．如图，腰长为22+2的等腰△ABC中，顶角∠A＝45°，D为腰AB上的一个动点，将△ACD沿CD折叠，点A落在点E处，当CE与△ABC的某一条腰垂直时，BD的长为 ．
18．如图，在Rt△ABC中，∠ABC=90°，∠A=30°，AB=3，BC=3，点D是边AC上一动点．连接BD，将△ABD沿BD折叠，得到△EBD，其中点A落在E处，BE交AC于点F，当△EDF为直角三角形时，EF长度是 ．
三、解答题（共2题，共13分）
19．等边△ABC中，BC=4，AH⊥BC于点H，点D为BC边上一动点，连接AD，点B关于直线AD的对称点为点E，连接AE，DE，CE．
（1）如图1，点E恰好落在AH的延长线上，则求∠BCE= °；
（2）过点D作DG∥AC交AB于点G，连接GE交AD于点F．
①如图2，试判断线段AF、EF和CE之间的数量关系，并说明理由：
②如图3，直线GE交AH于点M，连接BM，D点运动的过程中．当BM+GM取最小值时，请直接写出线段DG的长度．
20．如图，在矩形ABCD中，AB=5，AD=4，点E是BC边上一点，连接AE，将△ABE沿AE折叠得到△AFE，边AF，EF分别交CD于点M，N．
（1）求证：△ADM∽△NCE；
（2）当CE=FM时．
①求BE的长；
②若点P是AB边上的动点，连接PF，过点A作PF的垂线交线段BE于点Q，试探究PFAQ的值是否发生变化，若变化，请说明理由；若不变，请求出PFAQ的值．
四、实践探究题（共4题，共33分）
21．如图，在△ABC中，已知∠BAC =45°，AD⊥BC于点 D，BD=2，DC=3，求AD 的长.
小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题.
请按照小萍同学的思路，探究并解答下列问题：
（1）分别以 AB，AC 为对称轴，作出△ABD，△ACD的轴对称图形，点 D 的对称点分别为E，F，延长 EB，FC相交于点G.求证：四边形AEGF 是正方形.
（2）设 AD=x，利用勾股定理，建立关于 x的方程，求出 AD的长.
22．
（1）【初步探究】把矩形纸片ABCD如图①折叠，当点B的对应点B'在MN的中点时，填空：△EB'M △B'AN（“≌”或“∽”）．
（2）【类比探究】
如图②，当点B的对应点B'为MN上的任意一点时，请判断（1）中结论是否成立？如果成立，请写出证明过程；如果不成立，请说明理由．
（3）【问题解决】
在矩形ABCD中，AB=4，BC=6，点E为BC中点，点P为线段AB上一个动点，连接EP，将△BPE沿PE折叠得到△B'PE，连接DE，DB'，当△EB'D为直角三角形时，BP的长为 ．
23．【提出问题】如图1，在等腰△ABC中，AB=AC，分别以AB，AC为边作等边△ABE和等边△ACD，DC与BE相交于点F，连接CE．
（1）【初步探究】如图1，连接DB，求证：△ADB≌△AEC．
（2）【深入探究】如图2，将△ADC沿AC翻折得到△AD'C，连接D'E，BD'，类比(1)的探究方法发现：
结论①：_▲_≌△ABC；
结论②：BD'//CE．
请证明结论②．
（3）如图3、在(2)的情况下将线段AB沿AE翻折得到线段AB'，连接B'D'，AF，试判断线段B'D'与AF的位置关系．
24．
（1）【探究发现】如图①所示，在正方形ABCD中，E为AD边上一点，将△AEB沿BE翻折到△BEF处，延长EF交CD边于G点．求证：△BFG≌△BCG
（2）【类比迁移】如图②，在矩形ABCD中，E为AD边上一点，且AD=8，AB=6，将△AEB沿BE翻折到△BEF处，延长EF交BC边于点G，延长BF交CD边于点H，且FH=CH，求AE的长．
（3）【拓展应用】如图③，在菱形ABCD中，AB=6，E为CD边上的三等分点，∠D=60°，将△ADE沿AE翻折得到△AFE，直线EF交BC于点P，求CP的长．
答案解析部分
1．【答案】A
2．【答案】D
3．【答案】D
4．【答案】B
5．【答案】C
6．【答案】B
7．【答案】C
8．【答案】B
9．【答案】C
10．【答案】D
11．【答案】B
12．【答案】A
13．【答案】2116
14．【答案】12−362或3
15．【答案】214
16．【答案】60°；46
17．【答案】2或22
18．【答案】3−3或32
19．【答案】（1）15
（2）解：①AF=CE+EF；
理由如下：
如图，延长CE，AD交于点N；
设∠BAD=α，
由折叠性质得：∠EAD=∠BAD=α，AB=AE，GD=ED，∠AED=∠B=60°；
∴∠CAE=60°−2α，∠BAE=2α；
∵AB=AC=AE，
∴∠ACE=∠AEC=12(180°−∠CAE)=60°+α，∠DCE=∠ACE−∠ACB=α，
∵DG∥AC，
∴∠GDB=∠ACB=60°，∠BGD=∠BAC=60°，
∴∠AGD=∠GDC=180°−60°=120°，
∵∠AGD+∠AED=180°，
∴∠GDE+∠GAE=180°，
∴∠GDE=180°−∠BAE=180°−2α，
∴DG=DE，
∴∠DGE=∠DEG=α，
∴∠AEG=∠AED−∠DEG=60°−α，
∴∠CEG=∠AEC+∠AEG=60°+α+60°−α=120°，
∴∠FEN=60°；
∵∠EFN=∠EAD+∠AEG=α+60°−α=60°，
∴∠FEN=∠EFN=60°，
∴△EFN为等边三角形，
∴EF=EN，∠N=∠EFN=∠AFG=60°；
∵∠GDB=∠BGD=60°，
∴△BDG是等边三角形，
∴BD=BG，
∵AB=AC，
∴AG=CD，
∵∠GAF=∠DCN=α，∠N=∠AFG=60°
∴△AGF≌△CDN(AAS)，
∴AF=CN，
∴AF=CE+NE=CE+EF．
②DG=2．
20．【答案】（1）证明：∵矩形ABCD，
∴AB=CD=5，BC=AD=4，∠B=∠C=∠D=90°，
∵折叠，
∴△ABE≌△AFE，
∴∠F=∠B=90°，FE=BE，AB=AF，
∴∠AMD+∠DAM=∠FMN+∠FNM=90°，
又∠AMD=∠NMF，
∴∠DAM=∠FNM=∠CNE，
又∠C=∠D，
∴△ADM∽△NCE；
（2）解：①∵CE=FM，∠C=∠F=90°，∠FNM=∠CNE，
∴△FNM≌△CNE，
∴FN=CN，MN=EN，
∴FN+EN=CN+MN，即FE=CM=BE，
设CE=x，则BE=4−x，AM=5−x，DM=DC−CM=x+1，
在Rt△ADM中，AD2+DM2=AM2，
∴42+(x+1)2=(5−x)2，
解得x=23，
∴BE=BC−CE=103；
②PFAQ的值不变，值为1213．
理由：连接FQ，BF交AE于点O，过F作FH⊥AB于H，
∵折叠，
∴BO=FO，BF⊥AE，
∵∠ABE=90°，AB=5，BE=103，
∴AE=AB2+BE2=5313，
∴BO=AB⋅BEAE=101313，
∴BF=2BO=201313，
∵BF⊥AE，∠ABE=90°，
∴∠FBH=90°−∠OBE=∠AEB，
又∠FHB=∠ABE=90°，
∴△FBH∽△AEB，
∴FHAB=FBAE，即FH5=2013135313，
解得FH=6013，
∵FP⊥AQ，∠ABC=90°，
∴∠APF=90°−∠BAQ=∠AQB，
又∠FHP=∠ABQ=90°，
∴△FHP∽△ABQ，
∴FPAQ=FHAB=60135=1213．
21．【答案】（1）证明：由题意可得：△ABD≌△ABE，△ACD≌△ACF，∴∠DAB＝∠EAB，∠DAC＝∠FAC．
又∵∠BAC＝45°，
∴∠EAF＝2∠BAD+2∠DAC＝2∠BAC＝90°．
又∵AD⊥BC，
∠ADB＝∠ADC＝90°，
∴∠E＝∠ADB＝90°，∠F＝∠ADC＝90°．
∴四边形AEGF是矩形．
又∵AE＝AD，AF＝AD，
∴AE＝AF，
∴四边形AEGF是正方形；
（2）解：设AD＝x，则AE＝EG＝GF＝x．
∵BD＝2，DC＝3，
∴BE＝2，CF＝3，
∴BG＝x﹣2，CG＝x﹣3．
在Rt△BGC中，BG2+CG2＝BC2，
∴（x﹣2）2+（x﹣3）2＝52，
解得x1＝6，x2＝﹣1（舍去），
∴AD＝6．
22．【答案】（1）∽
（2）解：（1）中结论成立，理由如下：
∵四边形ABCD是矩形，
∴∠B=90°，
∵矩形纸片ABCD如图①折叠，
∴∠EB'A=∠B=90°，
∴∠EB'M=90°−∠AB'N=∠B'AN，
∵∠EMB'=90°=∠B'NA，
∴△EB'M∽△B'AN；
（3）94或1
23．【答案】（1）证明：∵△ACD和△ABE是等边三角形，
∴AD=AC，AB=AE，∠CAD=∠BAE=60°，
∴∠CAD−∠BAC=∠BAE−∠BAC，
∴∠BAD=∠CAE，
∴△ADB≌△AEC(SAS)；
（2）解：①∵△ACD是等边三角形，△ADC沿AC翻折得到△AD'C，
∴△AD'C是等边三角形，
同理(1)可知：△AED'≌△ABC(SAS)，
故答案为：△AED'；
②证明：如图，
作AW⊥CE，交BD'于V，
∵△ABE是等边三角形，
∴AB=AE，
∵AB=AC，
∴AC=AE，
∴∠CAW=∠EAW，
由①知：△AED'≌△ABC，
∴AB=AD'，∠BAC=∠EAD'，
∴∠BAC+∠CAW=∠EAD'+∠EAW，
∴∠BAW=∠D'AW，
∴AV⊥BD'，
∴BD'//CE；
（3）解：B'D'//AF，
∵AB=AC，
∴∠ABC=∠ACB，
∵△ACD和△ABE是等边三角形，
∴∠ABE=∠ACD=60°，
∴∠ABC−∠ABE=∠ACB−∠ABE，
∴∠CBF=∠BCF，
∴BF=CF，
∵AB=AC，AF=AF，
∴△ABF≌△ACF(SSS)，
∴∠BAF=∠CAF，
设∠BAF=∠CAF=α，
∴∠FAD'=∠CAF+∠CAD=α+60°，
∵线段AB沿AE翻折得到线段AB'，
∴∠EAB'=∠BAE=60°，
∵∠EAD'=BAC=2α，
∴∠B'AD'=∠EAB'−∠EAD'=60°−2α，
∵AB'=AB=AC=AD=AD'，
∴∠AD'B'=∠AB'D'=180°−∠B'AD'2=60°+α，
∴∠AD'B'=∠FAD'，
∴B'D'//AF．
24．【答案】（1）解：∵将ΔAEB沿BE翻折到ΔBEF处，四边形ABCD是正方形，
∴AB=BF，∠BFE=∠A=90°，
∴∠BFG=90°=∠C，
∵AB=BC=BF，BG=BG，
∴Rt△BFG≌Rt△BCG(HL)
（2）解：延长BH，AD交于Q，如图：
设FH=HC=x，
在Rt△BCH中，BC2+CH2=BH2，
∴82+x2=(6+x)2，
解得x=73，
∴DH=DC−HC=113，
∵∠BFG=∠BCH=90°，∠HBC=∠FBG，
∴ΔBFG∽ΔBCH，
∴BFBC=BGBH=FGHC，即68=BG6+73=FG73，
∴BG=254，FG=74，
∵EQ//GB，DQ//CB，
∴ΔEFQ∽ΔGFB，ΔDHQ∽ΔCHB，
∴BCDQ=CHDH，即8DQ=736−73，
∴DQ=887，
设AE=EF=m，则DE=8−m，
∴EQ=DE+DQ=8−m+887=1447−m，
∵ΔEFQ∽ΔGFB，
∴EQBG=EFFG，即1447−m254=m74，
解得m=92，
∴AE的长为92；
（3）解：（Ⅰ）当DE=13DC=2时，延长FE交AD于Q，过Q作QH⊥CD于H，如图：
设DQ=x，QE=y，则AQ=6−x，
∵CP//DQ，
∴ΔCPE∽ΔQDE，
∴CPDQ=CEDE=2，
∴CP=2x，
∵ΔADE沿AE翻折得到ΔAFE，
∴EF=DE=2，AF=AD=6，∠QAE=∠FAE，
∴AE是ΔAQF的角平分线，
∴AQAF=QEEF，即6−x6=y2①，
∵∠D=60°，
∴DH=12DQ=12x，HE=DE−DH=2−12x，HQ=3DH=32x，
在Rt△HQE中，HE2+HQ2=EQ2，
∴(1−12x)2+(32x)2=y2②，
联立①②可解得x=34，
∴CP=2x=32；
（Ⅱ）当CE=13DC=2时，延长FE交AD延长线于Q'，过D作DN⊥AB交BA延长线于N，如图：
同理∠Q'AE=∠EAF，
∴AQ'AF=Q'EEF，即6+x6=y4，
由HQ'2+HD2=Q'D2得：(32x)2+(12x+4)2=y2，
可解得x=125，
∴CP=12x=65，
综上所述，CP的长为32或65．