
03,2024学年江苏省徐州市邳州市运河中学九年级下学期独立作业(一模检测)数学模拟试题(无答案)
展开一、单选题
1.丰都正在创建全国文明城市,城市的英语单词city的大写字母是中心对称的是( )
A.B.C.D.
2.下列事件是必然事件的是( )
A.地球自转B.明天下雨C.时光倒流D.冬天飘雪
3.在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同. 其中的一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的( )
A.中位数B.众数C.平均数D.方差
4.实数a在数轴上对应的点如图所示,则a、−a、−1的大小关系正确的是( )
A.−1
A.a6÷a2=a3B.a23=a6C.a3⋅a4=a12D.a2−a=a
6.比3大且比14小的整数可以是( )
A.1B.3C.5D.7
7.割圆术是我国古代数学家刘微创造的一种求周长和面积的算法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”. 这一思想在数学领域中有广泛的应用.
例如:求3+3+3+⋯的值,则可以设x=3+3+3+…,根据上述思想方法有x=3+x,解方程得x=1+132;试用这个方法解决问题:1+13+132+131+…=( )
A.2B.32C.3D.54
8.如图,在平面直角坐标系中,抛物线y=−49x2+83x与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该P抛物线对称轴上一点,则3BC+5AC的最小值为( )
A.24B.25C.30D.36
二、填空题
9.每到春天柳絮漫天飞舞,据测定,柳絮纤维的直径为0.0000105m,该数值用科学记数法表示为 m.
10.函数y=1x−3中自变量x的取值范围是 .
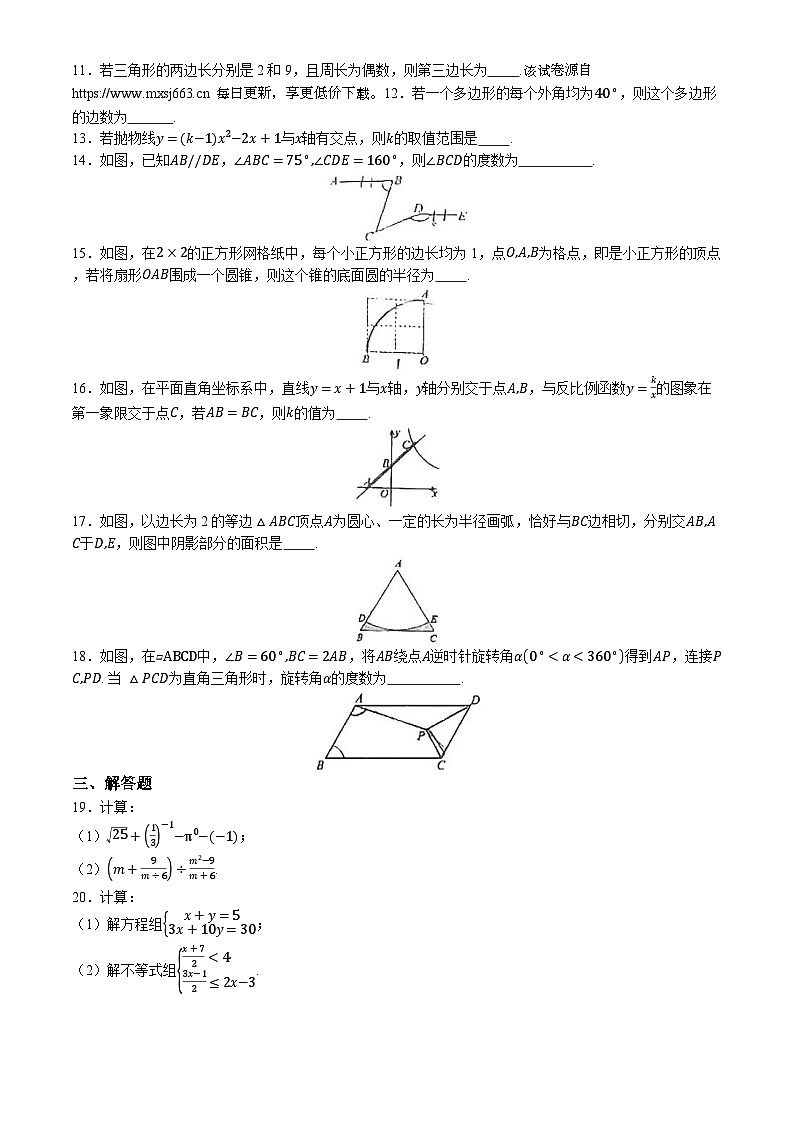
11.若三角形的两边长分别是2和9,且周长为偶数,则第三边长为 .该试卷源自 每日更新,享更低价下载。12.若一个多边形的每个外角均为40∘,则这个多边形的边数为 .
13.若抛物线y=k−1x2−2x+1与x轴有交点,则k的取值范围是 .
14.如图,已知AB//DE,∠ABC=75∘,∠CDE=160∘,则∠BCD的度数为 .
15.如图,在2×2的正方形网格纸中,每个小正方形的边长均为1,点O,A,B为格点,即是小正方形的顶点,若将扇形OAB围成一个圆锥,则这个锥的底面圆的半径为 .
16.如图,在平面直角坐标系中,直线y=x+1与x轴,y轴分别交于点A,B,与反比例函数y=kx的图象在第一象限交于点C,若AB=BC,则k的值为 .
17.如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是 .
18.如图,在▱ABCD中,∠B=60∘,BC=2AB,将AB绕点A逆时针旋转角α0∘<α<360∘得到AP,连接PC,PD. 当 △PCD为直角三角形时,旋转角α的度数为 .
三、解答题
19.计算:
(1)25+13−1−π0−−1;
(2)m+9m÷6÷m2−9m+6.
20.计算:
(1)解方程组x+y=53x+10y=30;
(2)解不等式组x+72<43x−12≤2x−3.
21.某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动. 某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
(1)在这次调查中,被调查的学生总人数为 人,在扇形统计图中,“乒乓球”的百分比为 %,
(2)请将条形统计图补充完整.
(3)如果学校有1800名学生,请估计全校学生中有多少人喜欢篮球项目.
(4)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表班级参加校篮球队,请列表格或画树状图求出所抽取的2名同学恰好都是女同学的概率.
22.疫情期间,我市新冠疫情在各地医疗队的帮助下,得到有效控制,我市准备向某客运公司租用A、B两种类型客车,陆续将支援队护送高城,已知每辆A型客车的载客人数比每辆B型客车多10人,如果单独租用A型客车护送900人,与单独租用B型客车护送700人所用车辆数一样多. (特别注明;本题中载客人数不考虑客车司机)
(1)问每辆A、B型客车分别可载多少人?
(2)某天,有630位支援人员需护送,客运公司根据需要,安排了A、B型汽车共16辆,每辆A型客车的租金为1200元,每辆B型客车的租金为1000元,总租金不超过17800元,问有哪几种租车方案,哪种方案较省钱,费用多少?
23.如图,在Rt△ABC中,∠A=90∘,∠C=30∘,BC=12.
(1)求作:以∠B为一个内角的菱形BDEF,使顶点E在AC边上;(要求;尺规作图,不写作法,保留作图痕迹)
(2)求菱形BDEF的边长.
24.如图,在△ABC中,D是边BC上一点,以BD为直径的⊙O经过点A,且∠CAD=∠ABC.
(1)请判断直线AC是否是⊙O的切线,并说明理由;
(2)若CD=2,CA=4,求弦AB的长.
25.无人机兴趣小组在操场上开展活动(如图),无人机在离地面D处,无人机测得操控者A的俯角为37∘,测得教学楼顶C处的俯角为45∘,经测量操控者A和教学楼BC距离为57米,若教学楼BC的高度为13米,求此时无人机距离地面的高度. (注:点A,B,C,D在同一平面上. 参考数据sin37∘≈0.60,cs37∘≈0.80,tan37∘≈0.75)
26.已知二次函数y=x2+bx+c.
(1)当c=−2b−4时,此函数图象与x轴有一个交点在y轴左侧,求b的取值范围;
(2)当b=1时,若存在实数x0,使得当x=x0时,y≤1成立,求c的最大值;
(3)b=−2mm>0,c=0时,此时函数在t≤x≤t+2的最大值为0,最小值为−4,求m和t的值.
27.
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,B在同一直线上,连接AE.
①线段AD,BE之间的数量关系为 ;
②∠AEB的度数为 ;
(2)拓展探究
如图2,△ACB和△AED均为等腰直角三角形,∠ACB=∠AED=90∘,点B,D,E在同一直线上,连接CE,求BDCE的值及∠BEC的度数;
(3)解决问题
如图3,在正方形ABCD中,CD=10,若点P满足PD=2,且∠BPD=90∘,请直接写出点C到直线BP的距离.
江苏省徐州市邳州市运河中学2023-2024学年九年级下学期独立作业(一模检测)数学试题: 这是一份江苏省徐州市邳州市运河中学2023-2024学年九年级下学期独立作业(一模检测)数学试题,共4页。
2023-2024学年江苏省徐州市邳州市运河中学数学九上期末经典试题含答案: 这是一份2023-2024学年江苏省徐州市邳州市运河中学数学九上期末经典试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
江苏省徐州市邳州市运河中学2023-2024学年八年级数学第一学期期末预测试题含答案: 这是一份江苏省徐州市邳州市运河中学2023-2024学年八年级数学第一学期期末预测试题含答案,共7页。试卷主要包含了下列关于的叙述中,错误的是,要使分式无意义,则的取值范围是,若分式的值为则,把2-4a2分解因式得等内容,欢迎下载使用。












