190，四川省成都市简阳市2022—2023学年下学期九年级期中数学试卷

这是一份190，四川省成都市简阳市2022—2023学年下学期九年级期中数学试卷，共22页。
A．﹣B．C．﹣D．
2．（3分）下列运算正确的是（ ）
A．a3•a2＝a5B．a+a2＝a3
C．6a2÷2a2＝3a2D．（3a2）3＝9a6
3．（3分）在每一个学子心中或许都梦想过自己心目中大学的模样，很多大学的校徽设计也会融入数学元素，下列大学的校徽图案是轴对称图形的是（ ）
A．清华大学B．北京大学
C．中国人民大学D．浙江大学
4．（3分）某芯片公司的最新一代CPU的时钟频率是5.2GHz，该公司1971年研制的世界第一枚4位微型处理器的时钟频率为0.000108GHz．将0.000108用科学记数法表示为（ ）
A．1.08×10﹣3B．1.08×10﹣4C．1.08×10﹣5D．10.8×10﹣5
5．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
6．（3分）下列计算正确的是（ ）
A．（3a3）÷（3a2）＝aB．2a3+2a2＝4a5
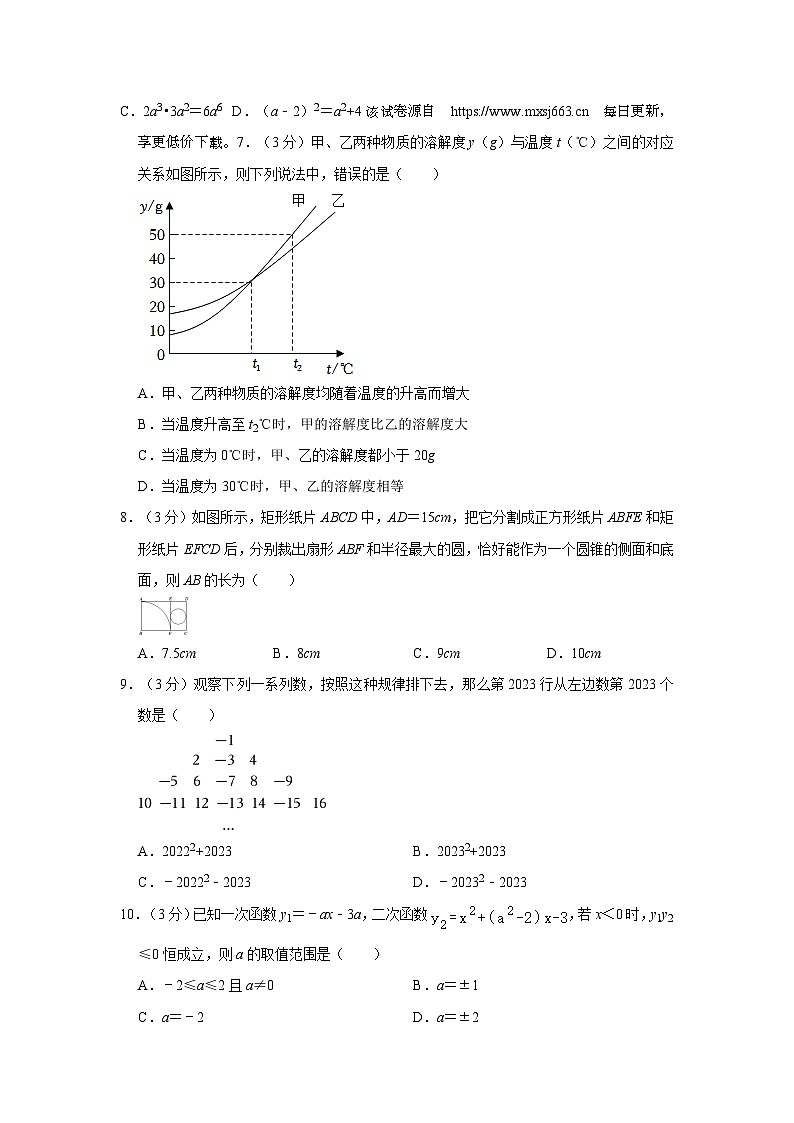
C．2a3•3a2＝6a6D．（a﹣2）2＝a2+4该试卷源自 每日更新，享更低价下载。7．（3分）甲、乙两种物质的溶解度y（g）与温度t（℃）之间的对应关系如图所示，则下列说法中，错误的是（ ）
A．甲、乙两种物质的溶解度均随着温度的升高而增大
B．当温度升高至t2℃时，甲的溶解度比乙的溶解度大
C．当温度为0℃时，甲、乙的溶解度都小于20g
D．当温度为30℃时，甲、乙的溶解度相等
8．（3分）如图所示，矩形纸片ABCD中，AD＝15cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（ ）
A．7.5cmB．8cmC．9cmD．10cm
9．（3分）观察下列一系列数，按照这种规律排下去，那么第2023行从左边数第2023个数是（ ）
A．20222+2023B．20232+2023
C．﹣20222﹣2023D．﹣20232﹣2023
10．（3分）已知一次函数y1＝﹣ax﹣3a，二次函数，若x＜0时，y1y2≤0恒成立，则a的取值范围是（ ）
A．﹣2≤a≤2且a≠0B．a＝±1
C．a＝﹣2D．a＝±2
二．填空题（共5小题，满分15分，每小题3分）
11．（3分）点A（﹣1，2）关于y轴的对称点坐标是 ．
12．（3分）分解因式：ab2﹣2ab+a＝ ．
13．（3分）若x，y满足方程组，则x﹣y＝ ．
14．（3分）在四边形ABCD中，∠ABC＝∠ADC＝90°，连接AC，点E为AC的中点，连接BE，DE．若，BC＝12，则△ABE的周长为 ．
15．（3分）如图，将反比例函数y＝（x＞0）的图象绕坐标原点（0，0）顺时针旋转45°，旋转后的图象与x轴相交于A点，若直线y＝x与旋转后的图象相交于B，则△OAB的面积为 ．
三．解答题（共8小题，满分75分）
16．（6分）先化简，再求值：÷（+6），其中a2﹣4a+3＝0．
17．（6分）解方程：．
18．（10分）如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1＝42°，求∠BDE的度数．
19．（9分）某乡镇新打造的“田园风光”景区今年计划改造一片绿化地，种植A、B两种花卉，已知3盆A种花卉和4盆B种花卉的种植费用为330元，4盆A种花卉和3盆B种花卉的种植费用为300元．
（1）每盆A种花卉和每盆B种花卉的种植费用各是多少元？
（2）若该景区今年计划种植A、B两种花卉共400盆，相关资料表明：A、B两种花卉的成活率分别为70%和90%，景区明年要将枯死的花卉补上相同的新花卉，但这两种花卉在明年共补的盆数不多于80盆，应如何安排这两种花卉的种植数量，才能使今年该项的种植费用最低？并求出最低费用．
20．（9分）某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2022年初的视力数据，并调取该批学生2021年初的视力数据，制成如下统计图（不完整）：
青少年视力健康标准
根据以上信息，请解答：
（1）分别求出被抽查的400名学生2021年初视力正常（类别A）的人数和2022年初轻度视力不良（类别B）的扇形圆心角度数．
（2）若2022年初该市有八年级学生8000人，请估计这些学生2022年初视力正常的人数比2021年初增加了多少人？
（3）国家卫健委要求，全国初中生视力不良率控制在69%以内．请估计该市八年级学生2022年初视力不良率是否符合要求？并说明理由．
21．（8分）第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行，我国冬奥选手取得了9块金牌、4块银牌、2块铜牌，为祖国赢得了荣誉，激起了国人对冰雪运动的热情．某地模仿北京首钢大跳台建了一个滑雪大跳台（如图1），它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成．图2是其示意图，已知：助滑坡道AF＝50米，弧形跳台的跨度FG＝7米，顶端E到BD的距离为40米，HG∥BC，∠AFH＝40°，∠EFG＝25°，∠ECB＝36°．求此大跳台最高点A距地面BD的距离是多少米（结果保留整数）．
（参考数据：sin40°≈0.64，cs40°≈0.77，tan40°≈0.84，sin25°≈0.42，cs25°≈0.91，tan25°≈0.47，sin36°≈0.59，cs36°≈0.81，tan36°≈0.73）
22．（12分）为了解决一些较为复杂的数学问题，我们常常采用从特殊到一般的思想，先从特殊的情形入手，从中找到解决问题的方法，已知四边形ABCD是⊙O的内接四边形，对角线AC与BD相交于点F．
【特殊情形】
（1）如图①，AC⊥BD，过圆心O作OE⊥CD，垂足为E．当BD是⊙O的直径时，求证：；
【一般情形】
（2）如图②，AC⊥BD，过圆心O作OE⊥CD，垂足为E，当BD不是⊙O的直径时，求证：；
【经验迁移】
（3）如图③，∠DFC＝45°，CD＝10，E为劣弧BC上的一点，CE＝AB，若H为DE的中点，连接CH，则∠DCE的度数为 ，CH的最小值为 ．
23．（15分）如图，在菱形ABCD中，∠ABC＝120°，点E是AD边的中点，点P是AB边上一动点（不与点A重合），连接PE并延长交CD的延长线于点Q，连接PD，AQ．
（1）求证：四边形APDQ是平行四边形；
（2）：
①当点P运动到何处时，四边形APDQ是矩形？写出理由；
②当点P运动到何处时，四边形APDQ是菱形？写出理由；
③点P在运动过程中，是否会存在某个位置，使得四边形APDQ是正方形？ ．（填“存在”或“不存在”）
2022-2023学年四川省成都市简阳市九年级（下）期中数学试卷
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）﹣的相反数是（ ）
A．﹣B．C．﹣D．
【解答】解：﹣的相反数是．
故选：B．
2．（3分）下列运算正确的是（ ）
A．a3•a2＝a5B．a+a2＝a3
C．6a2÷2a2＝3a2D．（3a2）3＝9a6
【解答】解：A．a3•a2＝a5，故本选项符合题意；
B．a和a2不能合并，故本选项不符合题意；
C．6a2÷2a2＝3，故本选项不符合题意；
D．（3a2）3＝27a6，故本选项不符合题意；
故选：A．
3．（3分）在每一个学子心中或许都梦想过自己心目中大学的模样，很多大学的校徽设计也会融入数学元素，下列大学的校徽图案是轴对称图形的是（ ）
A．清华大学B．北京大学
C．中国人民大学D．浙江大学
【解答】解：A，C，D选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
B选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：B．
4．（3分）某芯片公司的最新一代CPU的时钟频率是5.2GHz，该公司1971年研制的世界第一枚4位微型处理器的时钟频率为0.000108GHz．将0.000108用科学记数法表示为（ ）
A．1.08×10﹣3B．1.08×10﹣4C．1.08×10﹣5D．10.8×10﹣5
【解答】解：0.000108＝1.08×10﹣4．
故选：B．
5．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
【解答】解：由题意知，A选项中的图形是轴对称图形但不是中心对称图形，B选项中的图形是轴对称图形但不是中心对称图形，C选项中的图形即是中心对称图形又是轴对称图形，D选项中的图形是中心对称图形但不是轴对称图形．
故选：C．
6．（3分）下列计算正确的是（ ）
A．（3a3）÷（3a2）＝aB．2a3+2a2＝4a5
C．2a3•3a2＝6a6D．（a﹣2）2＝a2+4
【解答】解：A、（3a3）÷（3a2）＝a，原计算正确，故此选项符合题意；
B、2a3与2a2不是同类项，不能合并，原计算错误，故此选项不符合题意；
C、2a3•3a2＝6a5，原计算错误，故此选项不符合题意；
D、（a﹣2）2＝a2﹣4a+4，原计算错误，故此选项不符合题意；
故选：A．
7．（3分）甲、乙两种物质的溶解度y（g）与温度t（℃）之间的对应关系如图所示，则下列说法中，错误的是（ ）
A．甲、乙两种物质的溶解度均随着温度的升高而增大
B．当温度升高至t2℃时，甲的溶解度比乙的溶解度大
C．当温度为0℃时，甲、乙的溶解度都小于20g
D．当温度为30℃时，甲、乙的溶解度相等
【解答】解：由图象可知，A、B、C都正确，
当温度为t1℃时，甲、乙的溶解度都为30g，故D错误，
故选：D．
8．（3分）如图所示，矩形纸片ABCD中，AD＝15cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（ ）
A．7.5cmB．8cmC．9cmD．10cm
【解答】解：设圆锥的底面的半径为rcm，则DE＝2rcm，AE＝AB＝（15﹣2r）cm，
根据题意得，
解得，
所以．
故选：D．
9．（3分）观察下列一系列数，按照这种规律排下去，那么第2023行从左边数第2023个数是（ ）
A．20222+2023B．20232+2023
C．﹣20222﹣2023D．﹣20232﹣2023
【解答】解：由图可得，
第一行有1个数，
第二行有3个数，
第三行有5个数，
第四行有7个数，
……
则第n行有（2n﹣1）个数，
每一行的最后一个数字的绝对值是：n2，
∴第2023行从左边数第2023个数的绝对值是20222+2023，
∵图中的奇数都是负数，偶数都是正数，
∴第2023行从左边数第2023个数是﹣20222﹣2023．
故选：C．
10．（3分）已知一次函数y1＝﹣ax﹣3a，二次函数，若x＜0时，y1y2≤0恒成立，则a的取值范围是（ ）
A．﹣2≤a≤2且a≠0B．a＝±1
C．a＝﹣2D．a＝±2
【解答】解：∵一次函数解析式为y1＝﹣ax﹣3a＝﹣a（x+3），
∴一次函数经过定点（﹣3，0），
在中，当x＝0时，y2＝﹣3，
∴二次函数经过点（0，﹣3），
∵二次函数开口向上，
∴二次函数与x轴负半轴必有一个交点，且当自变量在这个交点和原点之间时，二次函数的函数值一定小于0，
∵x＜0时，y1y2≤0恒成立，
∴在二次函数与x轴负半轴的交点和原点之间一次函数的函数值大于等于0，同时还要满足在这个交点右边，一次函数的函数值小于0，
∴可知（﹣3，0）即为一次函数与二次函数的交点，且﹣a＞0，即a＜0，
∴9﹣3（a2﹣2）﹣3＝0，
解得a＝2（舍去）或a＝﹣2，
故选：C．
二．填空题（共5小题，满分15分，每小题3分）
11．（3分）点A（﹣1，2）关于y轴的对称点坐标是 （1，2） ．
【解答】解：由平面直角坐标系中关于y轴对称的点的坐标特点：横坐标相反数，纵坐标不变，
可得：点A关于y轴的对称点的坐标是（1，2）．
12．（3分）分解因式：ab2﹣2ab+a＝a（b﹣1）2．
【解答】解：ab2﹣2ab+a，
＝a（b2﹣2b+1），
＝a（b﹣1）2．
故答案为：a（b﹣1）2．
13．（3分）若x，y满足方程组，则x﹣y＝ ﹣1 ．
【解答】解：，
①×2﹣②得，5x＝5，
解得：x＝1；
把x＝1代入①得：4×1﹣y＝2，
解得y＝2，
∴x﹣y＝1﹣2＝﹣1．
故答案为：﹣1．
14．（3分）在四边形ABCD中，∠ABC＝∠ADC＝90°，连接AC，点E为AC的中点，连接BE，DE．若，BC＝12，则△ABE的周长为 18 ．
【解答】解：∵∠ABC＝∠ADC＝90°，点E为AC的中点，
∴AC＝2BE＝2DE＝2AE＝13，
∵BC＝12，
∴，
∴△ABE的周长为，
故答案为：18．
15．（3分）如图，将反比例函数y＝（x＞0）的图象绕坐标原点（0，0）顺时针旋转45°，旋转后的图象与x轴相交于A点，若直线y＝x与旋转后的图象相交于B，则△OAB的面积为 ．
【解答】解：设反比例函数y＝（x＞0）的图象上点E绕点O顺时针方向旋转45°得点A，过点E作EF⊥x轴于F，
设E（a，），
∵∠EOF＝45°，
∴EF＝OF，
∴a＝，
∵a＞0，
∴a＝，
∴OA＝OE＝，
作BC⊥x轴于C，△BOC是由KOH绕点O顺时针旋转45°得到的，
设B（x，），
∴OH＝OC＝x，
∴H（x，x），
∴过点H作GH⊥x轴于H，KG∥x轴，
∴△KGH是等腰直角三角形，
∵KH＝BC＝，
∴KG＝GH＝，
∴K（，），即K（，x），
∴•x＝5，
解得x＝或x＝﹣（舍），
∴＝，
∴BC＝，
∴S△AOB＝＝．
故答案为：．
三．解答题（共8小题，满分75分）
16．（6分）先化简，再求值：÷（+6），其中a2﹣4a+3＝0．
【解答】解：原式＝÷（+）
＝•
＝，
解方程a2﹣4a+3＝0，得a1＝1，a2＝3，
由题意得：a≠3，
当a＝1时，原式＝＝．
17．（6分）解方程：．
【解答】解：
方程两边同时乘以x﹣2，得：x+2+x﹣2＝2，
整理，得：2x＝2，
解得：x＝1，
经检验x＝1是原方程的解，
∴原方程的解为：x＝1．
18．（10分）如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1＝42°，求∠BDE的度数．
【解答】（1）证明：∵AE和BD相交于点O，
∴∠AOD＝∠BOE．
在△AOD和△BOE中，
∠A＝∠B，∴∠BEO＝∠2．
又∵∠1＝∠2，
∴∠1＝∠BEO，
∴∠AEC＝∠BED．
在△AEC和△BED中，
，
∴△AEC≌△BED（ASA）．
解：（2）∵△AEC≌△BED，
∴EC＝ED，∠C＝∠BDE．
在△EDC中，
∵EC＝ED，∠1＝42°，
∴∠C＝∠EDC＝69°，
∴∠BDE＝∠C＝69°．
19．（9分）某乡镇新打造的“田园风光”景区今年计划改造一片绿化地，种植A、B两种花卉，已知3盆A种花卉和4盆B种花卉的种植费用为330元，4盆A种花卉和3盆B种花卉的种植费用为300元．
（1）每盆A种花卉和每盆B种花卉的种植费用各是多少元？
（2）若该景区今年计划种植A、B两种花卉共400盆，相关资料表明：A、B两种花卉的成活率分别为70%和90%，景区明年要将枯死的花卉补上相同的新花卉，但这两种花卉在明年共补的盆数不多于80盆，应如何安排这两种花卉的种植数量，才能使今年该项的种植费用最低？并求出最低费用．
【解答】解：（1）设每盆A种花卉种植费用为x元，每盆B种花卉种植费用为y元，根据题意，
得：，
解得：，
答：每盆A种花卉种植费用为30元，每盆B种花卉种植费用为60元；
（2）设种植A种花卉的数量为m盆，则种植B种花卉的数量为（400﹣m）盆，种植两种花卉的总费用为w元，
根据题意，得：（1﹣70%）m+（1﹣90%）（400﹣m）≤80，
解得：m≤200，
w＝30m+60（400﹣m）＝﹣30m+24000，
∵﹣30＜0，
∴w随m的增大而减小，
当m＝200时，w的最小值＝﹣30×200+24000＝18000，
答：种植A、B两种花卉各200盆，能使今年该项的种植费用最低，最低费用为18000元．
20．（9分）某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2022年初的视力数据，并调取该批学生2021年初的视力数据，制成如下统计图（不完整）：
青少年视力健康标准
根据以上信息，请解答：
（1）分别求出被抽查的400名学生2021年初视力正常（类别A）的人数和2022年初轻度视力不良（类别B）的扇形圆心角度数．
（2）若2022年初该市有八年级学生8000人，请估计这些学生2022年初视力正常的人数比2021年初增加了多少人？
（3）国家卫健委要求，全国初中生视力不良率控制在69%以内．请估计该市八年级学生2022年初视力不良率是否符合要求？并说明理由．
【解答】解：（1）被抽查的400名学生2022年初轻度视力不良的扇形圆心角度数＝360°×（1﹣31.25%﹣24.5%﹣32%）＝44.1°．
该批400名学生2021年初视力正常人数＝400﹣48﹣91﹣148＝113（人）．
（2）该市八年级学生2022年初视力正常人数＝80000×31.25%＝25000（人）．
这些学生2021年初视力正常的人数＝80000×＝22600（人），
∴估计增加的人数＝25000﹣22600＝2400（人）．
∴估计这些学生2022年初视力正常的人数比2021年初增加了2400人．
（3）该市八年级学生2021年视力不良率＝1﹣31.25%＝68.75%．
∵68.75%＜69%．
∴该市八年级学生2021年初视力不良率符合要求．
21．（8分）第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行，我国冬奥选手取得了9块金牌、4块银牌、2块铜牌，为祖国赢得了荣誉，激起了国人对冰雪运动的热情．某地模仿北京首钢大跳台建了一个滑雪大跳台（如图1），它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成．图2是其示意图，已知：助滑坡道AF＝50米，弧形跳台的跨度FG＝7米，顶端E到BD的距离为40米，HG∥BC，∠AFH＝40°，∠EFG＝25°，∠ECB＝36°．求此大跳台最高点A距地面BD的距离是多少米（结果保留整数）．
（参考数据：sin40°≈0.64，cs40°≈0.77，tan40°≈0.84，sin25°≈0.42，cs25°≈0.91，tan25°≈0.47，sin36°≈0.59，cs36°≈0.81，tan36°≈0.73）
【解答】解：如图，过点E作EN⊥BC于点N，交HG于点M，则AB＝AH﹣EM+EN．
根据题意可知，∠AHF＝∠EMF＝∠EMG＝90°，EN＝40（米），
∵HG∥BC，
∴∠EGM＝∠ECB＝36°，
在Rt△AHF中，∠AFH＝40°，AF＝50，
∴AH＝AF•sin∠AFH≈50×0.64＝32（米），
在Rt△FEM和Rt△EMG中，设MG＝m米，则FM＝（7﹣m）米，
∴EM＝MG•tan∠EGM＝MG•tan36°≈0.73m，
EM＝FM•tan∠EFM＝FM•tan25°≈0.47（7﹣m），
∴0.73m＝0.47（7﹣m），
解得m≈2.7，
∴EM≈0.47（7﹣m）＝2.021（米），
∴AB＝AH﹣EM+EN≈32﹣2.021+40≈70（米）．
∴此大跳台最高点A距地面BD的距离约是70米．
22．（12分）为了解决一些较为复杂的数学问题，我们常常采用从特殊到一般的思想，先从特殊的情形入手，从中找到解决问题的方法，已知四边形ABCD是⊙O的内接四边形，对角线AC与BD相交于点F．
【特殊情形】
（1）如图①，AC⊥BD，过圆心O作OE⊥CD，垂足为E．当BD是⊙O的直径时，求证：；
【一般情形】
（2）如图②，AC⊥BD，过圆心O作OE⊥CD，垂足为E，当BD不是⊙O的直径时，求证：；
【经验迁移】
（3）如图③，∠DFC＝45°，CD＝10，E为劣弧BC上的一点，CE＝AB，若H为DE的中点，连接CH，则∠DCE的度数为 135° ，CH的最小值为 ．
【解答】（1）证明：∵OE⊥CD，
∴DE＝CE，
∵DO＝BO，
∴，
∵当BD是⊙O的直径时，AC⊥BD，
∴，
∴AB＝BC，
∴．
（2）证明：如图②，作直径DH交⊙O于点H，连接CH，AB，
同理（1），可得，
∵DH为直径，
∴∠DCH＝90°，
∵AC⊥DB，
∴∠DFA＝90°，
∵∠DHC＝∠DAC，
∴∠CDH＝90°﹣∠CHD＝90°﹣∠DAC＝∠ADB，
∴CH＝AB，
∴．
（3）解：延长EC，作HM⊥EC交于点M，如图③，③
∵CE＝AB，
∴∠CDE＝∠ADB，
∵∠DFC＝45°，
∴∠DAC+∠ADF＝45°，
∵∠DCE＝∠DAC，
∴∠DAC+∠ADF＝∠DEC+∠CDE＝45°，
∴∠ECD＝180°﹣（∠DEC+∠CDE）＝135°，
∵DM⊥CM，∠DCM＝45°，
∴△MCD为等腰直角三角形，
∵DC＝10，
∴，
观察图形，可知当CH⊥CE时，CH取最小值，
∵CH⊥CE，DM⊥CM，H为DE的中点，
∴HC是△DME的中位线，
∴．
故答案为：135°；．
23．（15分）如图，在菱形ABCD中，∠ABC＝120°，点E是AD边的中点，点P是AB边上一动点（不与点A重合），连接PE并延长交CD的延长线于点Q，连接PD，AQ．
（1）求证：四边形APDQ是平行四边形；
（2）：
①当点P运动到何处时，四边形APDQ是矩形？写出理由；
②当点P运动到何处时，四边形APDQ是菱形？写出理由；
③点P在运动过程中，是否会存在某个位置，使得四边形APDQ是正方形？ 不存在 ．（填“存在”或“不存在”）
【解答】（1）证明：∵四边形ABCD为菱形，
∴AB∥CQ，
∴∠QDA＝∠PAD，
∵点E是AD边的中点，
∴AE＝DE，
∵∠QED＝∠PEA
∴△APE≌△DQE（ASA）．
∴AP＝DQ．
∴四边形APDQ是平行四边形．
（2）解：①当点P运动到AB的中点时，如图，连接BD，
∵点P为AB的中点，
∴，
∵点E是AD边的中点，
∴AE＝AP，
∵∠ABC＝120°，
∴∠DAB＝60°，
∴△ABD为等边三角形，
∵点P为AB的中点，
∴DP⊥AB．
由（1）得四边形APDQ是平行四边形，
∴四边形APDQ是矩形．
②当点P与点B重合时，如图所示：
同①可证△ABD为等边三角形
∴AP＝DP．
由（1）得四边形APDQ是平行四边形，
∴四边形APDQ是菱形；
③由①②得，不存在点P，使得四边形APDQ是正方形，
故答案为：不存在．类别
视力
健康状况
A
视力≥5.0
视力正常
B
视力＝4.9
轻度视力不良
C
4.6≤视力≤4.8
中度视力不良
D
视力≤4.5
重度视力不良
类别
视力
健康状况
A
视力≥5.0
视力正常
B
视力＝4.9
轻度视力不良
C
4.6≤视力≤4.8
中度视力不良
D
视力≤4.5
重度视力不良