2024年甘肃省武威市凉州区凉州区中坝学联片教研中考三模数学试题

这是一份2024年甘肃省武威市凉州区凉州区中坝学联片教研中考三模数学试题，共11页。试卷主要包含了选择题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。

一、选择题(共30分)
1．（3分）-6的相反数是（ ）
A．6B．-6C．16D．-16
2．（3分）下列等式中成立的是（ ）
A．a8÷a4=a2B．(ab2)3=ab6C．3a+a=3a2D．a5⋅a=a6
3．（3分）某家具车间有32名工人，制作一种学生使用的课桌和椅子套装，已知1名工人在规定时间内可以制作课桌5件或制作椅子6件，1件课桌和2件椅子配成一套．为使在规定时间内制作出来的课桌和椅子恰好配套，求需要多少名工人制作课桌？需要多少名工人制作椅子？设x名工人制作课桌，y名工人制作椅子，则下列方程组正确的是（ ）
A．x+y=325x=6yB．x+y=322x=y
C．x+y=322×5x=6yD．x+y=325x=2×6y
4．（3分）如图，▱ABCD的对角线AC，BD交于点O，下列结论一定成立的是（ ）
A．OA=OBB．OA=OCC．OA⊥OBD．∠OBA=∠OBC
5．（3分）若 ab<0 且 a>b ，则函数 y=ax+b 的图象可能是（ ）
A． B． C． D．
6．（3分）如图，在⊙O中，直径AB与弦CD相交于点E，连接AC，若BC=BD，AC=CD=4，则tanC的值是（ ）
A．32B．33C．1D．3
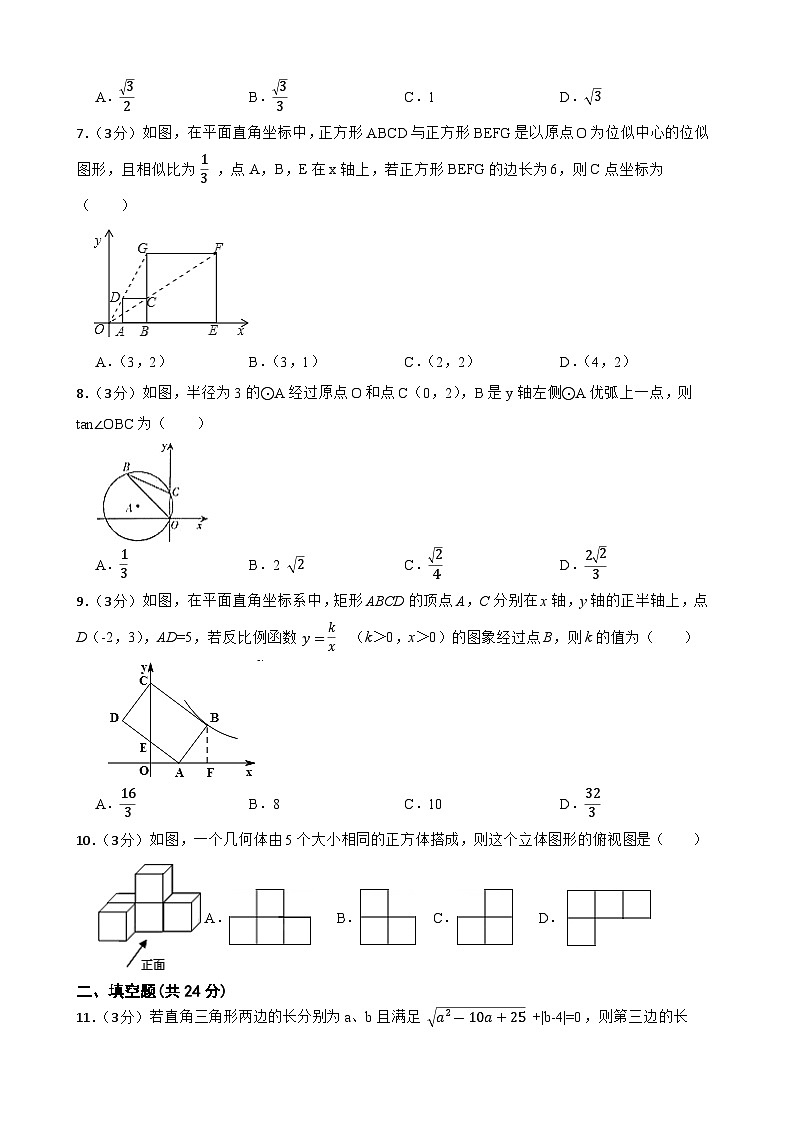
7．（3分）如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 13 ，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（ ）
A．（3，2）B．（3，1）C．（2，2）D．（4，2）
8．（3分）如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（ ）
A．13B．2 2C．24D．223
9．（3分）如图，在平面直角坐标系中，矩形ABCD的顶点A，C分别在x轴，y轴的正半轴上，点D（-2，3），AD=5，若反比例函数 y=kx （k＞0，x＞0）的图象经过点B，则k的值为（ ）
A．163B．8C．10D．323
10．（3分）如图，一个几何体由5个大小相同的正方体搭成，则这个立体图形的俯视图是（ ）
A． B． C． D．
二、填空题(共24分)
11．（3分）若直角三角形两边的长分别为a、b且满足 a2-10a+25 +|b-4|=0，则第三边的长是 。
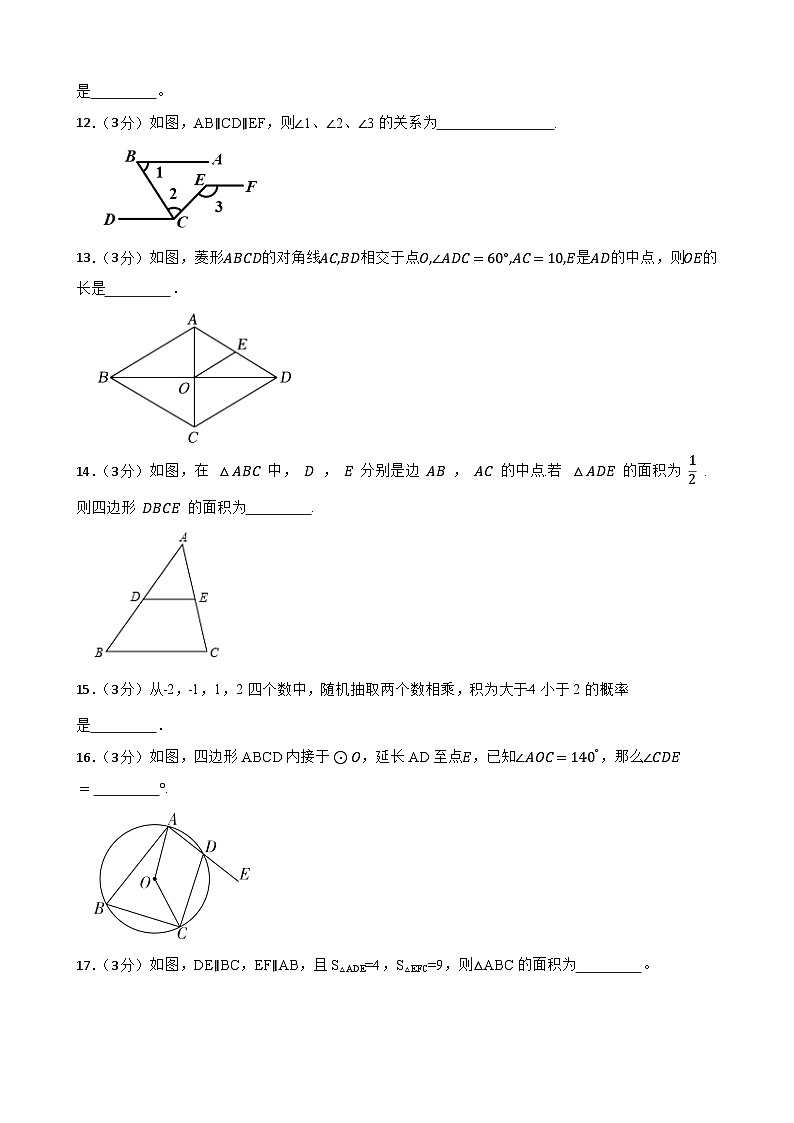
12．（3分）如图，AB∥CD∥EF，则∠1、∠2、∠3的关系为 .
13．（3分）如图，菱形ABCD的对角线AC,BD相交于点O,∠ADC=60°,AC=10,E是AD的中点，则OE的长是 ．
14．（3分）如图，在 △ABC 中， D ， E 分别是边 AB ， AC 的中点.若 △ADE 的面积为 12 .则四边形 DBCE 的面积为 .
15．（3分）从﹣2，﹣1，1，2四个数中，随机抽取两个数相乘，积为大于﹣4小于2的概率是 ．
16．（3分）如图，四边形ABCD内接于⊙O，延长AD至点E，已知∠AOC=140°，那么∠CDE= °.
17．（3分）如图，DE∥BC，EF∥AB，且S△ADE=4，S△EFC=9，则△ABC的面积为 。
18．（3分）已知点(x1,y1)，(x2,y2)，(x3,y3)在反比例函数y=k2+1x的图象上，且x1<0三、计算题(共8分)
19．（8分）（1）（4分）计算：(13)-1+4-6sin45°+|2-2|
（2）（4分）解不等式组：3(x-1)≤5x+34x-23<1-13x
四、作图题(共6分)
20．（6分）在如图所示的正方形网格中，每个小正方形边长为1个单位，小正方形的顶点称为格点，点A、B、C均在格点上．要求只用无刻度直尺画图，并保留画图痕迹．
（1）（2分）在图①中的线段AC上找一点D，连结BD，使SΔABC=2SΔABD；
（2）（2分）在图②中的线段BC上找一点E，连结AE，使SΔABC=3SΔACE；
（3）（2分）在图③中的△ABC内部找一点H，连结AH、BH，使SΔABC=3SΔABH．
五、解答题(共52分)
21．（6分）如图，AB∥CD，且AB=CD，连接AC，与BD相交于点O．求证：△ABO≌△CDO．
22．（6分）如图，矩形 ABCD 的对角线 AC ， BD 交于点 O ，且 DE//AC ， AE//BD ，连接 OE .求证： OE⊥AD .
23．（8分）2023年杭州亚运会吉祥物一开售，就深受大家的喜爱．某旅游商场以每件50元的价格购进某款亚运会吉祥物，以每件80元的价格出售，每日可售出200件．从7月份起，商场决定采用降价促销的方式回馈顾客，经调查，发现该吉祥物每降价1元，日销售量就会增加20件．设售价为x(x≥50)元，日销售量为y件．
（1）（2分）直接写出日销售量为y（件）与每件售价x（元）之间的函数关系式 ；
（2）（3分）为了让顾客得到更大的实惠，当该吉祥物售价定为多少元时，日销售利润达7500元？
（3）（3分）该商场如何定价，才能使日销售利润最大？最大利润是多少元？
24．（8分）如图，在菱形ABCD中，AB=6，∠ABC=120°，△DEF为正三角形，点E，F分别在菱形的边AB，BC．上滑动，且点E、F不与点A，B，C重合，BD与EF交于点G．
（1）（4分）证明：当点E，F在边AB，BC上滑动时，总有AE=BF．
（2）（4分）当BF=2时，求BG的长．
25．（6分）在一次综合实践活动中，某小组对一建筑物进行测量，如图，在山坡坡脚C处测得该建筑物顶端B的仰角为60°，测得建筑物顶端B的仰角为30°，已知山坡坡度i=3:4，即tanθ=34，请你帮助该小组计算建筑物的高度AB．（结果精确到0.1m，参考数据：3≈1.732）
26．（8分）如图，⊙O是△ABC 的外接圆，AB是⊙O的直径，延长BC 至点D， 使(CD=BC,连接AD交⊙O于点E，连接BE，过点 C作 CF∥BE交AD 于点 F.
（1）（4分）求证：CF是⊙O的切线；
（2）（4分）若EF=1，AE=3，求BD的长.
27．（10分）如图，二次函数y=-x2+bx+c的图象与x轴相交于点A和点C(1，0)，交y轴于点B(0，3)．
（1）（3分）求此二次函数的解析式；
（2）（3分）设二次函数图象的顶点为P，对称轴与x轴交于点Q，求四边形AOBP的面积（请在图1中探索）；
（3）（4分）二次函数图象的对称轴上是否存在点M，使得△AMB是以AB为底边的等腰三角形？若存在，请求出满足条件的点M的坐标；若不存在，请说明理由（请在图2中探索）．
答案
1-5 ADCBA 6-10 DACDD
11．3或 41 12．∠1+∠2=∠3 13．5 14．32 15．12
16．70 17．25 18．y2>y3>y1
19．（1）7-42； （2）不等式组的解集为-3≤x<1
20．（1）
（2）
（3）
21．∵AB∥CD，
∴∠A=∠C，∠B=∠D，
在△ABO与△CDO中，
∠A=∠CAB=CD∠B=∠D，
∴△ABO≌△CDO(ASA)．
22． ∵DE//AC，AE//BD ，
∴ 四边形 AODE 是平行四边形，
∵ 四边形 ABCD 是矩形，
∴OA=OD=12AC=12BD ，
∴ 平行四边形 AODE 是菱形，
∴OE⊥AD .
23．（1）y=-20x+1800(x≥50)
（2）由题意得：(x-50)(-20x+1800)=7500，
整理得：x2-140x+4875=0，
解得：x1=65,x2=75，
∵为了让顾客得到更大的实惠，
∴x2=75舍去，
∴x=65，
该吉祥物售价为65元时，日销售利润达7500元．
（3）设日销售利润为W元，由题意得：W=(x-50)(-20x+1800)
=-20(x-70)2+8000，
∵-20<0，
∴当x=70时，W最大=8000（元）；
每件售价为70元时，可使日销售利润最多．
24．（1）∵四边形ABCD是菱形，
∴AD∥BC，AD=AB，BD平分∠ABC，
∵∠ABC=120°，
∴∠A=180°-∠ABC=60°，
∴△ABD是等边三角形
∴AD=BD，∠A=∠DBC=∠ADB=60°，
∵△DEF为正三角形，
∴∠EDF=60°，
∴∠ADE=60°-∠EDB=∠BDF，
∴△ADE≌△BDF，
∴AE=BF；
（2）由（1）可知BF=AE=2，
∵AB=AD=6，
∴BE=4
∵∠A+∠ADE=∠DEB=∠DEF+∠BEG，∠A=∠DEF=60°，
∴∠ADE=∠BEG．
又∵∠A=∠EBG=60°，
∴△ADE∽△BEG，
∴ADBE=AEBG，即64=2BG，
∴BG=43．
25．过点D作DE⊥AC，垂足为E，作DF⊥AB，垂足为F，
则四边形DEAF为矩形，
∴DE=AF，DF=AE，
在Rt△DEC中，tanθ=DEEC=34，
设DE=3x米，则CE=4x米，
∵DE2+CE2=DC2，
∴(3x)2+(4x)2=400，
∴x=4或x=-4（舍去），
∴DE=AF=12米，CE=16米，
设BF=y米，
∴AB=BF+AF=(12+y)米，
在Rt△DBF中，∠BDF=30°，
∴DF=BFtan30°=y33=3y（米），
∴AE=DF=3y米，
∴AC=AE-CE=(3y-16)米，
在Rt△ABC中，∠ACB=60°，
∴tan60°=ABAC=12+yy-16=3，
解得：y=6+83，
经检验：y=6+83是原方程的根，
∴AB=BF+AF=18+83≈31.9（米），
∴建筑物的高度AB约为31.9米．
26．（1）如解图， 连接 OC，
∵ AB 是⊙O 的直径，
∴ BE⊥AD.
∵ OA=OB，BC=CD，
∴ C 为 BD 中点，OC 为△ABD 中位线，
∴ OC∥AD，
∴ BE⊥OC.
∵ CF∥BE，
∴ CF⊥OC.
∵ OC 是⊙O 的半径，
∴ CF 是⊙O 的切线：
（2）∵ AB 是⊙O 的直径，
∴∠ACD=∠ACB=90°.
∵∠AEB=90°，CF∥BE，
∴∠CFD=∠CFE=90°.
∴∠ACD=∠CFD.
∵∠ADC=∠CDF，
∴△ACD∽△CFD，
∴ADCD=CDFD,即CD2=AD⋅FD.
∵CF∥BE， BC=CD，
∴DF=EF=1.
∵AE=3，
∴AD=AE+EF+DF=5，
∴CD2=5×1=5,即CD=5(负值已舍去)，
∴BD=2CD=25.
27．（1）将点C（1，0）与B（0，3）分别代入y=-x2+bx+c得，
-1+b+c=0c=3，
∴b=-2c=3，
∴y=-x2-2x+3；
（2）如图，连接OP，
∵y=-x2-2x+3=-(x+1)2+4，
∴P(-1，4)，
∴PQ=4，OQ=1，
由-x2-2x+3=0得，x1=1，x2=-3，
∴OA=3，
∴S四边形AOBP=S△AOP+S△BOP=12OA⋅PQ+12OB⋅OQ=12×3×4+12×3×1=152
（3）设M(-1，m)，
∵OA=3，
∴A(-3，0)，
由AM2=BM2得[(-3)-(-1)]2+m2=(-1)2+(m-3)2，
∴m=l，
∴M(-1，1)．