2024年甘肃省武威市武威十四中联片教研中考三模数学试题

这是一份2024年甘肃省武威市武威十四中联片教研中考三模数学试题，共12页。试卷主要包含了选择题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。
一、选择题(共30分)
1．（3分）-2的相反数是（ ）
A．12B．-12C．-2D．2
2．（3分）下列计算正确的是（ ）
A．2+3=5B．23-3=2C．2×3=6D．12÷3=2
3．（3分）若关于x的一元二次方程(a-2)x2+2x-1=0有两个不相等的实数根，则a的取值范围是（ ）
A．a≠2B．a≥1且a≠2C．a>1且a≠2D．a>1
4．（3分）如图所示，在Rt△ABC中，∠ACB＝90°，∠A＝30°，CD是斜边AB上的高，BD＝2，那么AB等于（ ）
A．5B．6C．8D．12
5．（3分）如图，有六根长度相同的木条，小明先用四根木条制作了能够活动的菱形学具，他先将该活动学具调成图1所示菱形，测得∠B＝60°，对角线AC＝10cm，接着将该活动学具调成图2所示正方形，最后用剩下的两根木条搭成了如图3所示的图形，连接BE，则图3中△BCE的面积为（ ）
A．503 cm2B．50cm2C．253 cm2D．25cm2
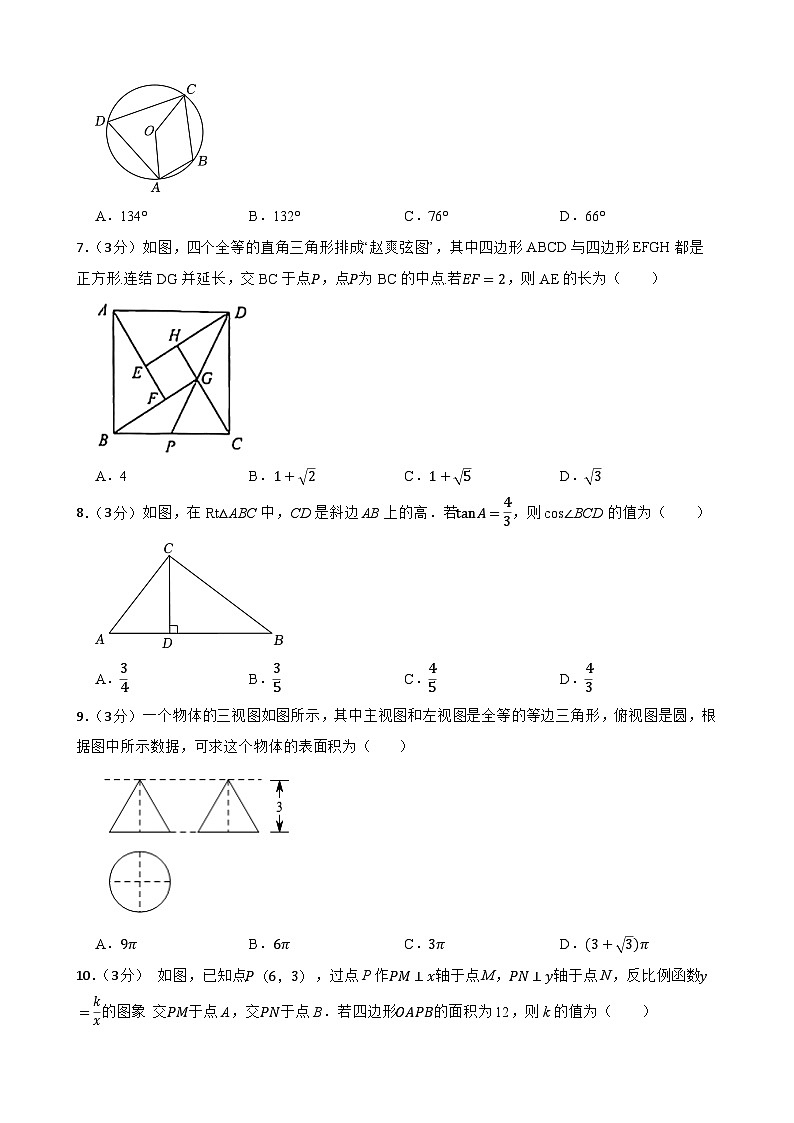
6．（3分）如图，四边形ABCD是⊙O的内接四边形，若∠ABC＝114°，则∠AOC的度数为（ ）
A．134°B．132°C．76°D．66°
7．（3分）如图，四个全等的直角三角形排成“赵爽弦图”，其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长，交BC于点P，点P为BC的中点.若EF=2，则AE的长为（ ）
A．4B．1+2C．1+5D．3
8．（3分）如图，在Rt△ABC中，CD是斜边AB上的高．若tanA=43，则cs∠BCD的值为（ ）
A．34B．35C．45D．43
9．（3分）一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆，根据图中所示数据，可求这个物体的表面积为（ ）
A．9πB．6πC．3πD．(3+3)π
10．（3分） 如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数y=kx的图象 交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k的值为（ ）
A．6B．-6C．12D．-1
二、填空题(共24分)
11．（3分） 已知方程|x-2y+4|+(2x+5y-1)2=0，则(x+y)2024=
12．（3分） 若二次根式2-x有意义，则实数x的取值范围是 ．
13．（3分）如图，已知a∥b，∠1=70°，∠2=40°，则∠3= 度.
14．（3分）如图，过⊙O外一点P作圆的切线PA，PB，点A，B为切点，AC为直径，设∠P=m°，∠C=n°，则m，n的等量关系为 .
15．（3分）如图▱ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为 ．
16．（3分） 如图，在△ABC中，点D、E、F分别在AB、BC、AC上，且DE∥AC，EF∥AB，AFFC=12，若AB=12，则BD的长为 ．
17．（3分）已知一次函数y=2x-3与y=kx(k是常数，k≠0)的图象的交点坐标是(2，1)，则方程组y=2x-3y=kx的解是 .
18．（3分）如图，△ABC中，∠BAC=60°，∠ABC=45°，AB= 2 ，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于E、F，连接EF，则线段EF长度的最小值为 ．
三、计算题(共8分)
19．（8分）计算：
（1）（4分）计算：2sin60°+|﹣3|﹣ 12 ﹣（ 13 ）﹣1
（2）（4分）先化简，再求值 x2-1x2+2x÷x-1x-xx+2 ，其中x满足方程x2+4x﹣5=0．
四、作图题(共4分)
20．（4分）如图，在边长为1的小正方形组成的网格中建立直角坐标系，小正方形的顶点为格点，△ABC与△EFG的顶点都在格点上.
（1）（2分）作△A1B1C1，使△A1B1C1与△ABC关于原点O成中心对称.
（2）（2分）已知△ABC与△EFG关于点P成中心对称，请在图中画出点P的位置，并写出该点的坐标.
五、解答题(共54分)
21．（6分）如图，点A，F，C，D在同一直线上，BC∥EF，AF＝DC，BC＝EF．求证：AB∥DE．
22．（6分）如图，在四边形ABCD中，AB∥CD，过点D作∠ADC的角平分线交AB于点E，连接AC交DE于点O，AD∥CE．
（1）（3分）求证：四边形AECD是菱形；
（2）（3分）若AD=10，△ACD的周长为36，求菱形AECD的面积．
23．（8分）甘肃临夏州积石山县发生6.2级地震，牵动着全国人民的心，时值严冬寒潮，当地气温极低，急需防寒保暖物资．某市紧急组织救灾物资援助灾区，安排大、小货车共16辆，分别从A、B两个仓库运送180吨物资到积石山灾区．已知每辆大货车可装15吨物资，每辆小货车可装9吨物资，在每辆货车都装满的情况下，这16辆货车恰好可以装完这批物资．这两种货车的运费如下表．
（1）（4分）大、小货车各有多少辆？
（2）（4分）若要安排货车中的10辆从A仓库出发，其余的6辆从B仓库出发．设从A仓库出发的大货车有m辆，这16辆货车的总运费为W，求W的最小值．
24．（8分）某学校为了了解本校1200名学生的课外阅读的情况，现从各年级随机抽取了部分学生，对他们一周的课外阅读时间进行了调整，井绘制出如下的统计图①和图②，根据相关信息，解答下列问题：
（1）（2分）本次接受随机抽样调查的学生人数为 ，图①中 m 的值为 ；
（2）（3分）求本次调查获取的样本数据的众数、中位数和平均数；
（3）（3分）根据样本数据，估计该校一周的课外阅读时间大于 6h 的学生人数．
25．（8分）小明同学在综合实践活动中对本地的一座古塔进行了测量.如图，他在山坡坡脚P处测得古塔顶端M的仰角为 60° ，沿山坡向上走25m到达D处，测得古塔顶端M的仰角为 30° .已知山坡坡度 i=3：4 ，即 tanθ=34 ，请你帮助小明计算古塔的高度ME.（结果精确到0.1m，参考数据： 3≈1.732 ）
26．（8分） 如图，AB是⊙O的直径，过圆上点C的直线CD交BA延长线于点D，且∠DCA=∠B．
（1）（4分）求证：CD是⊙O的切线；
（2）（4分）若CD=2，tan∠B=12，求AB的长．
27．（10分）如图，点 B ， C 分别在 x 轴和 y 轴的正半轴上， OB ， OC 的长分别为 x2-8x+12=0 的两个根 (OC>OB) ，点 A 在 x 轴的负半轴上，且 OA=OC=3OB ，连接 AC ．
（1）（3分）求过 A ， B ， C 三点的抛物线的函数解析式；
（2）（3分）点 P 从点 C 出发，以每秒2个单位长度的速度沿 CA 运动到点 A ，点 Q 从点 O 出发，以每秒1个单位长度的速度沿 OC 运动到点 C ，连接 PQ ，当点 P 到达点 A 时，点 Q 停止运动，求 S△CPQ 的最大值；
（3）（4分）M 是抛物线上一点，是否存在点 M ，使得 ∠ACM=15° ？若存在，请求出点 M 的坐标；若不存在，请说明理由．
答案
1-5 DCCCD 6-10 BCBAA
11．1 12．x≤2 13．70 14．m+2n=180 15．15
16．4 17．x=2y=1 18．32
19．（1） 3 ；（2）原式=- 13 ．
20．（1）
△A1B1C1即为所求作的三角形.
（2）
点P（-3，-1）.
21．∵BC∥EF，
∴∠ACB＝∠EFD，
∵AF＝CD，
∴AC＝DF，
在△ABC和△DEF中，
AC=DF∠ACB=∠DFEBC=EF，
∴△ABC≌△DEF（SAS），
∴∠A＝∠D，
∴AB∥DE．
22．（1）∵AB∥CD ，AD∥E ，
∴四边形AECD 为平行四边形，
∵AB∥CD ，
∴∠AED=∠CDE ，
∵DE 平分∠ADC ，
∴∠ADE=∠CDE ，
∴∠AED=∠ADE ，
∴AD=AE ，
∴四边形AECD 是菱形．
（2）如图，∵四边形AECD 是菱形，
∴AC⊥DE ，OD=OE ，OA=OC ，AD=CD=10 ，
∵△ACD 的周长为36，
∴AC=C△ACD-AD-CD=36-10-10=16 ，
即OA=OC=8 ．
在Rt△AOD 中，∠AOD=90° ，由勾股定理得，
∴DO2+AO2=AD2 ，即DO2=102-82 ，
∴DO=6 ．
∴DE=12 ．
∴S菱形AECD=12AC⋅DE=12×12×16=96 ．
23．（1）设大货车有x辆，小货车有y辆．
由题意，得x+y=1615x+9y=180，
解得x=6y=10，
大货车有6辆，小货车有10辆．
（2）∵从A仓库出发的大货车有m辆，
∴从A仓库出发的小货车有(10-m)辆，从B仓库出发的大货车有(6-m)辆，从B仓库出发的小货车有10-(10-m)=m辆．
由题意，得W=1500m+1000(10-m)+1800(6-m)+1200m=-100m+20800．
∵-100OB ，∴点 B 的坐标为 (2，0) ，点 C 的坐标为 (0，6) ．
∵OA=OC ，∴点 A 的坐标为 (-6，0) ．
设抛物线的函数解析式为 y=ax2+bx+c ，
将点 A ， B ， C 的坐标代入 y=ax2+bx+c 中，
得 36a-6b+c=04a+2b+c=0c=6 ，解得 a=-12b=-2c=6 ．
∴过 A ， B ， C 三点的抛物线的函数解析式为 y=-12x2-2x+6 ．
（2）∵OA=OC ，∴∠ACO=45° ．
由题意得 PC=2t ， CQ=6-t ，∴|xP|=PC⋅sin45°=2t ．
∴S△CPQ=12×CQ×|xP|=12×(6-t)×2t=-22(t2-6t) ．
∵-22