广东省河源市东源县2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份广东省河源市东源县2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含广东省河源市东源县2023-2024学年七年级下学期期中数学试题原卷版docx、广东省河源市东源县2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
第一部分选择题（共30分）
一、单选题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合要求的．）
1. 计算（ ）
A. 1B. 0C. D.
【答案】A
【解析】
【分析】本题主要考查了0指数幂计算，根据任何非零数的0指数幂都为1即可求解．
【详解】解：，
故选：A．
2. 水中涟漪（圆形水波）不断扩大，记它的半径为r，则圆周长C与r的关系式为．下列判断正确的是（ ）
A. 2是变量B. 是变量C. r是变量D. C是常量
【答案】C
【解析】
【分析】根据变量与常量的定义分别判断，并选择正确的选项即可．
【详解】解：2与π为常量，C与r为变量，
故选：C．
【点睛】本题考查变量与常量的概念，能够熟练掌握变量与常量的概念为解决本题的关键．
3. 如图，直线，交于点，若，则等于（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查了对顶角的性质，根据对顶角相等即可得到．
【详解】解：∵，
∴，
故选：D．
4. 下列运算正确的是（ ）
A. a•a2＝a2B. 5a•5b＝5abC. a5÷a3＝a2D. 2a+3b＝5ab
【答案】C
【解析】
【分析】根据同底数幂的乘除法则、整式的混合运算法则进行计算即可．
【详解】A. a•a2＝a3，错误；
B. 5a•5b＝25ab，错误；
C. a5÷a3＝a2 ，正确；
D. 2a+3b＝2a+3b，错误；
故答案为：C．
【点睛】本题考查了整式的混合运算问题，掌握同底数幂的乘除法则、整式的混合运算法则是解题的关键．
5. 已知弹簧的长度y cm与所挂物体的质量x kg之间有如下关系，则（ ）
A. y随x的增大而增大B. 质量每增加1kg，弹簧的长度增加0.5cm
C. 不挂物体时，弹簧的长度为6cmD. 质量为6kg时，弹簧的长度为8.5cm
【答案】C
【解析】
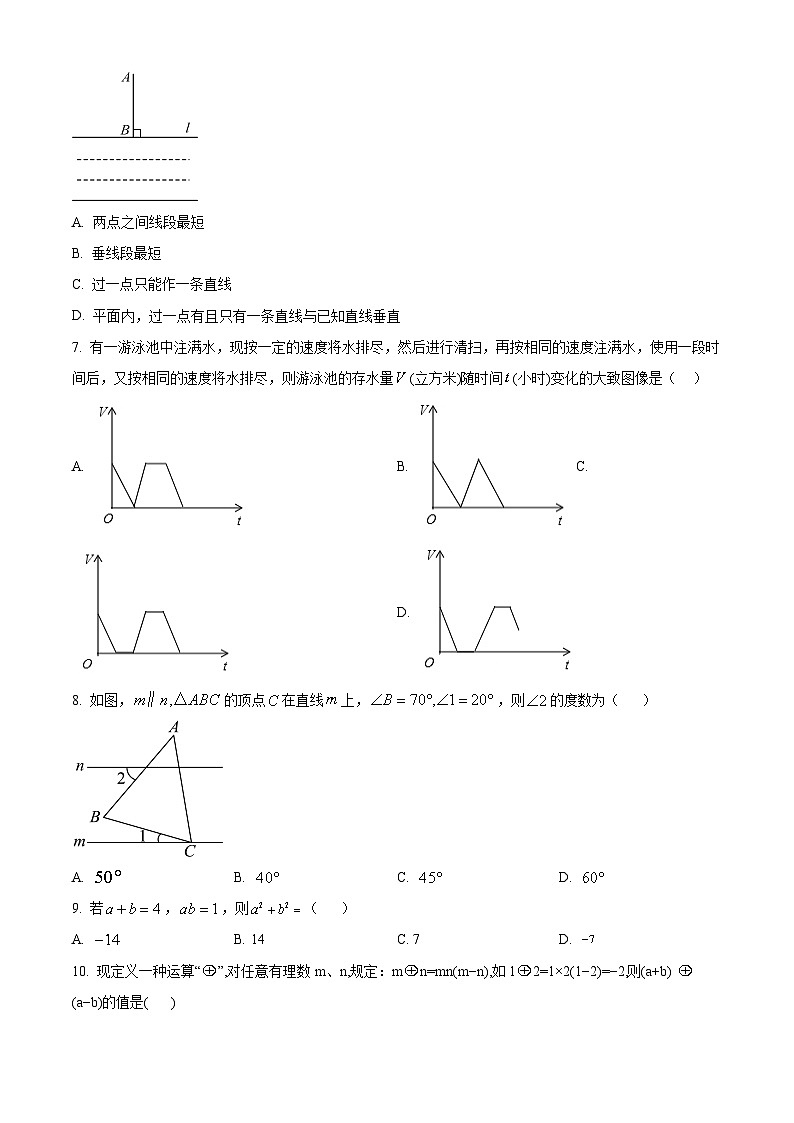
6. 如图，计划把河水l引到水池A中，先作AB⊥l，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是（ ）
A. 两点之间线段最短
B. 垂线段最短
C. 过一点只能作一条直线
D. 平面内，过一点有且只有一条直线与已知直线垂直
【答案】B
【解析】
【详解】【分析】根据垂线段的性质：垂线段最短可得答案．
【详解】计划把河水l引到水池A中，先作AB⊥l，垂足为B，然后沿AB开渠，能使所开的渠道最短，
这样设计的依据是垂线段最短，
故选B．
【点睛】本题主要考查了垂线段的性质．关键是熟练掌握垂线段最短．
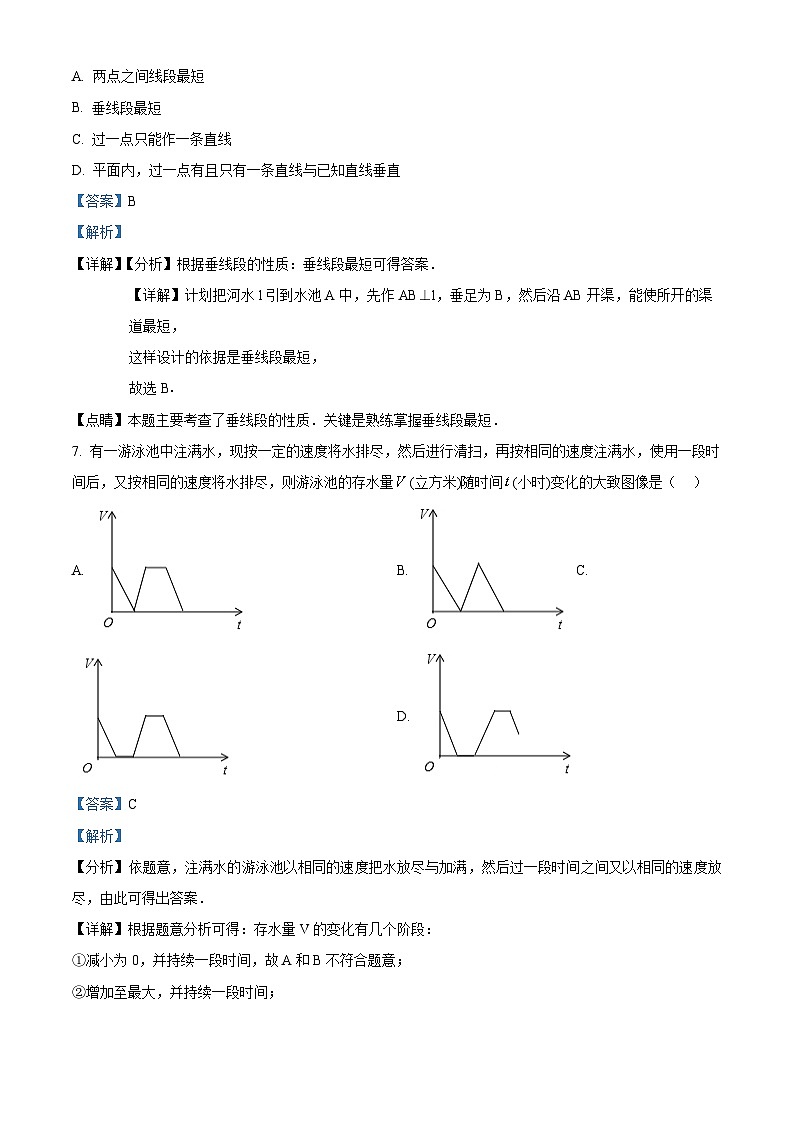
7. 有一游泳池中注满水，现按一定的速度将水排尽，然后进行清扫，再按相同的速度注满水，使用一段时间后，又按相同的速度将水排尽，则游泳池的存水量(立方米)随时间(小时)变化的大致图像是（ ）
A. B. C.
D.
【答案】C
【解析】
【分析】依题意，注满水的游泳池以相同的速度把水放尽与加满，然后过一段时间之间又以相同的速度放尽，由此可得出答案．
【详解】根据题意分析可得：存水量V的变化有几个阶段：
①减小为0，并持续一段时间，故A和B不符合题意；
②增加至最大，并持续一段时间；
③减小为0，故D不符合题意．
故选C．
【点睛】本题考查正确理解函数图象与实际问题的关系，理解问题的过程，能够通过图象得到函数是随自变量的增大，知道函数值是增大还是减小，通过图象得到函数是随自变量的增大或减小的快慢．
8. 如图，的顶点在直线上，，则的度数为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了平行线的性质，熟练掌握平行线的性质，并能进行推理论证与计算是解决问题的关键．作，由平行线的性质得出，由平行公理推出，由平行线的性质得出即可．
【详解】解：作，如图，
，
，
，，
，
．
故选：A
9. 若，，则（ ）
A. B. 14C. 7D.
【答案】B
【解析】
【分析】本题主要考查完全平方公式的变形，熟练掌握完全平方公式是解题的关键．
【详解】解：，，
．
故选：B．
10. 现定义一种运算“”,对任意有理数m、n,规定：mn=mn(m−n),如12=1×2(1−2)=−2,则(a+b) (a−b)的值是( )
A. 2ab2−2b2B. 2ab2+2b2C. 2a2b−2b3D. 2ab−2ab2
【答案】C
【解析】
【分析】根据题目中的新运算可以求得（a+b）（a-b）的值，本题得以解决．
【详解】∵mn=mn(m−n)，
∴(a+b) (a−b)=(a+b)(a−b)[(a+b)−(a−b)]=(a2−b2)×2b=2a2b−2b3，
故选C.
【点睛】本题考查整式的混合运算和有理数的混合运算，解题的关键是掌握整式的混合运算和有理数的混合运算.
第二部分非选择题（共90分）
二、填空题（本大题共6小题，每小题3分，满分18分．）
11. 比较大小：_____．
【答案】
【解析】
【分析】本题考查了比较数的大小，幂的运算，先计算，及的值，再比较两个数的大小即可，解题关键是掌握幂的运算法则．
【详解】解：，，
又，
，
故答案为：．
12. 谚语“冰冻三尺非一日之寒”体现了冰的厚度随时间变化的一个变化过程，在该变化过程中因变量是________．
【答案】冰的厚度
【解析】
【分析】、根据变量与常量的定义进行判定即可得出答案．
【详解】解：谚语“冰冻三尺非一日之寒”体现了冰的厚度随时间变化的一个变化过程，在该变化过程中因变量是冰的厚度．
故答案为：冰的厚度．
【点睛】本题考查了变量与常量的定义，熟练掌握知识点是解题的关键．
13. 石墨烯是现在世界上最薄的纳米材料，其理论厚度仅有0.00000000034米，将数据0.00000000034用科学记数法表示为_____________．
【答案】3.4×10-10
【解析】
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【详解】解：0．00000000034=3.4×10-10．
故答案为：3.4×10-10．
【点睛】本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
14. 已知，则的余角等于______．
【答案】25
【解析】
【分析】本题考查了余角：若两角和为，则两角互余；根据余角的定义计算求值即可；
【详解】解：∵，
∴的余角等于，
故答案为：25；
15. 一个长方形的周长为，其中它的长为自变量，宽为因变量，则与之间的关系式为_________．
【答案】##
【解析】
【分析】本题主要考查列关系式，根据长方形的周长为14列出等式，移项使y在等号左边，其余在等号右边即可．
【详解】解：∵长方形的周长为，长为，宽为，
∴，
∴，
故答案为：．
16. 如图是一组有规律的图案，它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，…依此规律，第n个图案中有__________个白色圆片（用含n的代数式表示）

【答案】
【解析】
【分析】由于第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，，可得第个图案中有白色圆片的总数为．
【详解】解：第1个图案中有4个白色圆片，
第2个图案中有6个白色圆片，
第3个图案中有8个白色圆片，
第4个图案中有10个白色圆片，
，
∴第个图案中有个白色圆片．
故答案为：．
【点睛】此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．解题关键是总结归纳出图形的变化规律．
三、解答题（一）（本大题共3小题，第17题和第18题各4分，第19题6分，共14分．解答应写出文字说明、证明过程或演算步骤．）
17. 计算：．
【答案】1
【解析】
【分析】本题主要考查了负整数指数幂，含乘方的有理数混合计算，先计算乘方和负整数指数幂，再去绝对值，最后计算加减法即可．
【详解】解：原式
．
18. 计算：．
【答案】
【解析】
【分析】本题主要考查多项式除以单项式，掌握多项式除以单项式的运算法则是解题的关键．
【详解】解：
．
19. 已知：如图，点P为的边上一点，
（1）求作：过点P作，使得；（要求保留作图痕迹）
（2）直线CP和OA的位置关系是 ．
【答案】（1）见详解 （2）平行
【解析】
【分析】（1）先以O点为圆心，任意长为半径画弧交OA、OB于E、F，再以P点为圆心，OE为半径画弧交PB于M，然后分别以M、F为圆心，EF为半径画弧，两弧相交于点N，则直线PN满足条件；
（2）由同位角相等，两直线平行，即可得到结论成立．
【小问1详解】
解：如图所示：
【小问2详解】
证明：∵，
∴∥，
故答案为：平行．
【点睛】本题考查了作图——复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解题的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
四、解答题（二）（本大题共3小题，第20题6分，第21题8分，第22题10分，共24分．解答应写出文字说明、证明过程或演算步骤．）
20. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
（1）上述两个变量之间的关系中，哪个是自变量？哪个是因变量？
（2）用 h（cm）表示这摞碗的高度，用 x（只）表示这摞碗的数量，请用含有 x 的代数式表示 h；
（3）若这摞碗的高度为 11.2cm，求这摞碗的数量．
【答案】（1）碗的数量是自变量，高度是因变量；
（2）h=1.2x+2.8；
（3）7只；
【解析】
【分析】（1）根据碗的高度随着碗的数量变化而改变，即可判断；
（2）求出每只碗增加的高度即可解答；
（3）根据（2）h和x的关系式代入求值即可；
【小问1详解】
解：通过表格所列举的变量可知，碗的数量是自变量，高度是因变量；
【小问2详解】
解：由表格可知，每增加一只碗，高度增加1.2cm，
∴h=4+1.2（x-1）=1.2x+2.8，
∴h=1.2x+2.8；
【小问3详解】
解：∵h=1.2x+2.8，
∴11.2=1.2x+2.8，
解得：x=7，
∴碗的数量是7只；
【点睛】本题考查了函数的概念：一般地，在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数．
21. 先化简，再求值：，其中，．
【答案】．
【解析】
【分析】本题主要考查了整式化简求值，先根据平方差公式，完全平方公式，单项式乘以多项式的计算法则去括号，然后合并同类项化简，最后代值计算即可．
【详解】解：
当，时，则原式．
22. 如图1，点、、在同一条直线上，，平分，从点出发画一条射线，使得，请画出满足条件的射线，并求出的度数．
（1）如图2，已画出射线的第一种位置，请将解题过程补充完整：
解：因为，，
所以_________________，，
因为平分，
所以____________，
因为，
所以__________________．
（2）请在图3中画出射线的第二种位置．
【答案】（1）；；；；；；；
（2）见解析，
【解析】
【分析】本题主要考查了几何图形中角度的计算，角平分线的定义：
（1）根据平角的定义求出，再由角平分线的性质得出，最后根据即可得出答案；
（2）先画图，再根据平角的定义求出，再由角平分线的性质得出，最后根据即可得出答案．
【小问1详解】
解：因为，，
所以，
因为平分，
所以，
因为，
所以．
故答案为：；；；；；；；；
【小问2详解】
解：如图所示， 射线即为所求：
因为，
所以．
因为平分，
所以．
因为，
所以．
五、解答题（三）（本大题共3小题，第23题10分，第24题和第25题各12分，共34分．解答应写出文字说明、证明过程或演算步骤．）
23. “天宫课堂”开讲，传播普及空间科学知识，激发了广大青少年不断追求“科学梦”的热情．小明在周末从家骑自行车到本市科技馆探索科技的奥秘，他骑行了一段时间后，在某路口等待红绿灯，待绿灯亮起后继续向科技馆方向骑行，在快到科技馆时突然发现钥匙不见了，于是他着急地原路返回，在刚刚等红绿灯的路口处找到了钥匙，然后继续前往科技馆．小明离科技馆的距离与离家的时间的关系如图12所示，请根据图中提供的信息回答下列问题：
（1）小明家到本市科技馆的距离是______；
（2）小明等待红绿灯所用的时间为______；
（3）图中点表示的意义是______．
（4）小明在整个途中，哪个时间段骑车速度最快？
【答案】（1）3000
（2）2 （3）小明离家时，离科技馆的距离为
（4）小明在速度最快
【解析】
【分析】本题主要考查了从函数图象获取信息：
（1）根据题意和函数图象可以得到小明家到晋中市科技馆的距离；
（2）根据函数图象可知线段，路程没有发生变化，此时在等红绿灯；
（3）根据题意，可知C点横坐标为12，纵坐标为600，据此即可求解；
（4）分别求得各时段的速度即可求解．
【小问1详解】
解：根据题意和函数图象可知小明家到本市科技馆的距离为
故答案为：3000；
【小问2详解】
解：根据函数图象可知线段路程没有发生变化，
∴小明等待红绿灯所用的时间为，
故答案为：2；
【小问3详解】
由题意得，点C的实际意义为小明离家时，离科技馆的距离为；
故答案为：小明离家时，离科技馆的距离为；
【小问4详解】
由图可知，
小明在时间段内速度为： ，
小明在时间段内速度为：，
小明在时间段内速度为：，
小明在时间段内速度为：，
∴小明时间段内速度最快．
24. 如图，边长为的大正方形中有一个边长为的小正方形，把图①中的阴影部分拼成一个长方形（如图②所示）．
（1）上述操作能验证的等式是（ ）（请选择正确的一个）．
A．；B．；C．
（2）请应用（1）中的等式完成下列各题：
①已知，，则______；
②计算：．
③计算：．
【答案】（1）A （2）①4；②1257；③
【解析】
【分析】本题考查平方差公式，掌握平方差公式的结构特征是正确应用的前提．
（1）分别表示图1和图2中阴影部分的面积即可得出答案；
（2）①利用平方差公式化简计算即可；
②利用平方差公式将原式转化为即可．
③利用平方差公式将解答即可．
【小问1详解】
解：图1中阴影部分的面积为两个正方形的面积差，即，
图2中的阴影部分是长为，宽为的长方形，因此面积为，
所以有，
故答案为：A；
【小问2详解】
解：①，，，
；
②原式
；
③原式
．
25. 问题情景：
如图1，，，，求的度数．
（1）天天同学看过图形后立即口答出：，请你补全他的推理依据．
如图2，过点作，
，
．
（______）
（______）．（______）
，
，
问题迁移：
（2）如图3，，当点在、两点之间运动时，，，求与，之间有何数量关系？请说明理由．
（3）在（2）的条件下，如果点在、两点外侧运动时（点与点、、三点不重合），请你直接写出与，之间的数量关系．
【答案】（1）；；两直线平行，同旁内角互补；（2），理由见解析；（3）①当在延长线时，；②当在延长线时，．
【解析】
【分析】本题主要考查了平行线的性质与判定：
（1）根据平行线的判定与性质填写即可；
（2）过P作交于E，推出，根据平行线的性质得出，，即可得出答案；
（3）画出图形（分两种情况①点P在的延长线上，②点P在的延长线上），根据平行线的性质得出，，即可得出答案．
【详解】解：（1）如图2，过点作，
，
．
（两直线平行，同旁内角互补）
．（两直线平行，同旁内角互补）
，
，
故答案为：；；两直线平行，同旁内角互补；
（2），理由如下：
如图3所示，过P作交于E，

∵，
∴，
∴，，
∴；
（3）当P在BA延长线时，如图4所示：

过P作交于E，
同（2）可知：∠α=∠DPE，∠β=∠CPE，
∴；
当P在延长线时，如图5所示：

同（2）可知：，，
∴．
综上所述，与、之间的数量关系为：当P在BA延长线时，或当P在延长线时，．
x/kg
0
1
2
3
4
5
y/cm
6
6.5
7
7.5
8
8
数量/只
1
2
3
4
5
…
高度/cm
4
5.2
6.4
7.6
88
…