广东省汕头市金平区汕樟中学2023-2024学年八年级下学期期中数学试题（原卷版+解析版）

这是一份广东省汕头市金平区汕樟中学2023-2024学年八年级下学期期中数学试题（原卷版+解析版），文件包含广东省汕头市金平区汕樟中学2023-2024学年八年级下学期期中数学试题原卷版docx、广东省汕头市金平区汕樟中学2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

（时间：120分钟 满分：120分）
一、选择题（每小题3分，共30分）
1. 若式子有意义，则a的取值范围是（ ）
A B. C. D.
【答案】C
【解析】
【分析】本题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．根据二次根式有意义的条件可得，再解不等式即可．
【详解】解：根据题意，得，
∴，
故选：C．
2. 下列各组数据中，不是勾股数的是（ ）
A. 3，4，5B. 5，12，13C. 6，8，10D. 2，3，4
【答案】D
【解析】
【分析】本题考查了勾股数，根据：“一组正整数，且满足两个较小的数的平方和等于最大数的平方，这样的一组数叫做勾股数”，进行判断即可．
【详解】解：A、，是勾股数，不符合题意；
B、，是勾股数，不符合题意；
C、，是勾股数，不符合题意；
D、，不是勾股数，符合题意；
故选D．
3. 下列计算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】根据二次根式的加减运算法则以及乘除运算法则即可求出答案．
【详解】解：A、与不是同类二次根式，故不能合并，故A不符合题意．
B、与不是同类二次根式，故不能合并，故B不符合题意．
C、原式，故C不符合题意．
D、原式，故D符合题意．
故选：D．
【点睛】本题考查二次根式，解题的关键是熟练运用二次根式的加减运算以及乘除运算．
4. 菱形和矩形都具有的性质是（ ）
A. 对角线互相平分B. 有一组邻边相等
C. 对角线相等D. 对角线互相垂直
【答案】A
【解析】
【分析】利用矩形的性质和菱形的性质可求解．
【详解】∵矩形的对角线相等且互相平分，菱形的对角线垂直且互相平分，
∴菱形和矩形都具有的性质为对角线互相平分，
故选：A．
【点睛】本题考查的是矩形和菱形的性质，熟练掌握矩形和菱形的性质是解决本题的关键.
5. 下列二次根式中是最简二次根式的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据最简二次根式的定义判断即可．
【详解】解：A、，不是最简二次根式，本选项不符合题意；
B、是最简二次根式，本选项符合题意；
C、不是最简二次根式，本选项不符合题意；
D、不是最简二次根式，本选项不符合题意；
故选：B．
【点睛】此题考查了最简二次根式，被开方数不含分母、被开方数中不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．
6. 如图，在中，对角线与相交于点，，，，则以下结论不正确的是（ ）

A B.
C. D. 的面积为6
【答案】D
【解析】
【分析】根据平行四边形的性质，勾股定理，进行求解后，判断即可．
【详解】解：∵在中，，，
∴，，
∵，
∴，
∴，
∴，的面积为，
∴，
∴；
综上：选项A、B、C正确，不符合题意；选项D错误，符合题意；
故选D．
【点睛】本题考查平行四边形的性质，勾股定理．熟练掌握平行四边形的性质，是解题的关键．
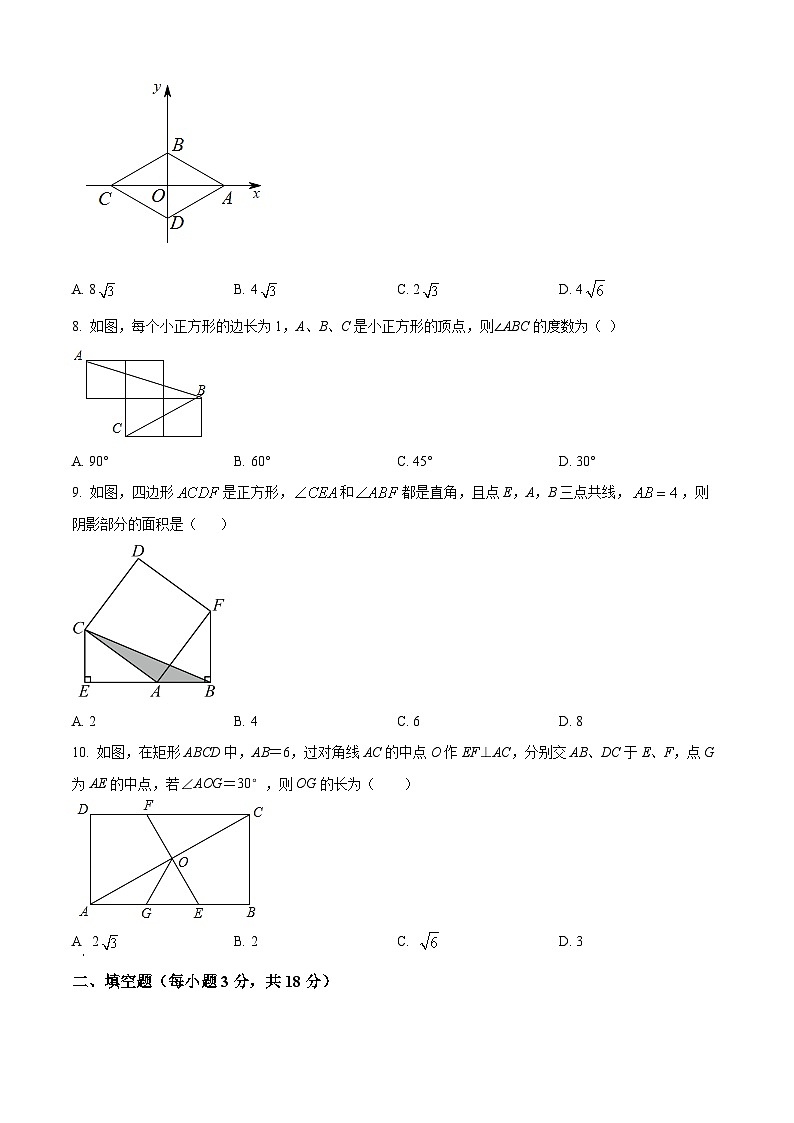
7. 如图，四边形为菱形，，两点的坐标分别是，，点，在坐标轴上，则菱形的周长等于（ ）
A. 8B. 4C. 2D. 4
【答案】A
【解析】
【分析】由勾股定理可求AB的长，由菱形的性质可求解．
【详解】解：∵A，B两点的坐标分别是（3，0），，
∴OB＝，OA＝3，
∴AB＝，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝DA＝，
∴菱形ABCD的周长等于＝4×＝8，
故选：A．
【点睛】本题考查了菱形的性质，坐标与图形的性质，掌握菱形的性质是本题的关键．
8. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（ ）
A. 90°B. 60°C. 45°D. 30°
【答案】C
【解析】
【分析】根据勾股定理即可得到AB，BC，AC的长度，进行判断即可．
【详解】解：连接AC，如图：
根据勾股定理可以得到：AC=BC=，AB=．
∵（）2+（）2=（）2．
∴AC2+BC2=AB2．
∴△ABC是等腰直角三角形．
∴∠ABC=45°．
故选C．
【点睛】本题考查了勾股定理的应用，熟练掌握其性质是解题的关键．
9. 如图，四边形是正方形，和都是直角，且点E，A，B三点共线，，则阴影部分的面积是（ ）
A. 2B. 4C. 6D. 8
【答案】D
【解析】
【分析】本题考查了正方形的性质，全等三角形的判定与性质，证明得出，即可求解．
【详解】∵四边形是正方形，
∴，，
∵和都是直角，
∴，，
∴，
∴，
∴阴影部分的面积是，
故选：D．
10. 如图，在矩形ABCD中，AB＝6，过对角线AC的中点O作EF⊥AC，分别交AB、DC于E、F，点G为AE的中点，若∠AOG＝30°，则OG的长为（ ）
A. 2B. 2C. D. 3
【答案】B
【解析】
【分析】根据30°直角三角形的性质和直角三角形斜边上中线的性质，利用方程思想可求出OG的长度.
【详解】解：∵EF⊥AC，
∴∠AOE＝90°，
在Rt△AOE中，G是AE的中点，
∴OG＝AE＝AG＝GE，
∴∠OAG＝∠AOG＝30°，
∴∠OGE＝60°，
∴△OGE是等边三角形，
设OG＝x＝OE，
∴AE＝2x，AO＝x，
∵O是AC的中点，
∴AC＝2AO＝x，
在Rt△ABC中，
BC＝AC＝x，
由勾股定理得，
AB2+BC2＝AC2，
∴，
解得x＝2.
∴OG＝2，
故选：B.
【点睛】本题主要考查30°直角三角形的性质以及直角三角形斜边上的中线等于斜边的一半，解题的关键在于巧设x，利用勾股定理构建方程解决．
二、填空题（每小题3分，共18分）
11. 比较大小：________.
【答案】
【解析】
【详解】解：∵，
∴
故答案为：
12. 已知三角形的三边为2，2，，则这个三角形是____三角形．
【答案】等腰直角
【解析】
【分析】本题考查了勾股定理逆定理，二次根式的乘法计算，根据，且，即可判断出这个三角形是等腰直角三角形．
【详解】解：，且，
这个三角形是等腰直角三角形，
故答案为：等腰直角．
13. 如图，在平行四边形中，平分，，，则的周长是__________．
【答案】16
【解析】
【分析】根据角平分线的定义以及两直线平行，内错角相等求出∠CDE=∠CED，再根据等角对等边的性质可得CE=CD，然后利用平行四边形对边相等求出CD、BC的长度，再求出▱ABCD的周长．
【详解】解：∵DE平分∠ADC，
∴∠ADE=∠CDE，
∵▱ABCD中,AD∥BC，
∴∠ADE=∠CED，
∴∠CDE=∠CED，
∴CE=CD，
∵在▱ABCD中，AD=5，BE=2，
∴AD=BC=5，
∴CE=BC−BE=5−2=3，
∴CD=AB=3，
∴▱ABCD的周长=5+5+3+3=16．
故答案为：16．
【点睛】本题考查了对边平行，对边相等，角平分线的定义，角对等边的性质，是基础题，准确识图并熟练掌握性质是解题的关键．
14. 计算________．
【答案】
【解析】
【分析】本题考查了负整数指数幂，分母有理数，利用二次根式的性质化简，根据负整数指数幂先化成分式，在分母有理化，利用二次根式的性质化简即可．
【详解】解：，
故答案为：．
15. 在中，，．若点 P在边AC上移动，则线段BP的最小值是 ________ ．
【答案】
【解析】
【分析】作AD⊥BC于点D，如图，根据等腰三角形的性质和勾股定理可求出AD，根据垂线段最短可知：当BP⊥AC时，BP最小，再利用三角形的面积求解即可．
详解】解：作AD⊥BC于点D，如图，
∵，，
∴BD=CD=3，AD=，
根据垂线段最短可知：当BP⊥AC时，BP最小，
则由S△ABC=，可得，解得；
即线段BP的最小值是．
故答案为：．
【点睛】本题考查了等腰三角形的性质、勾股定理以及三角形的面积等知识，正确理解题意、熟练掌握上述知识是解题的关键．
16. 如图，平行四边形的周长为，自顶点A作于点E，于点F．若，则________．
【答案】
【解析】
【分析】本题考查了平行四边形的性质，勾股定理，面积法，首先根据面积法求出的长，再在，中利用勾股定理求出的长，进而求出的长求解即可．
【详解】∵平行四边形的周长为56，
，
，
，
，
，
解得：，
，
，
在中，，
在中，，
，，
，
故答案为：．
三、解答题（一）（每小题6分，共18分）
17. 计算：．
【答案】
【解析】
【分析】本题考查了实数的运算，利用二次根式的性质，零指数幂，负整数指数幂的意义化简，然后合并即可．
【详解】解：原式
．
18. 如图，在中，于E，点F在边上，，求证：四边形是矩形．
【答案】见解析．
【解析】
【分析】由平行四边形的性质得出AD∥BC，AD＝BC，再证AF＝CE，得四边形AECF是平行四边形，然后证∠AEC＝90°，即可得出结论．
【详解】证明：四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵BE＝DF，
∴AD−DF＝BC−BE，
即AF＝CE，
∵AF∥CE，
∴四边形AECF是平行四边形，
又∵AE⊥BC，
∴∠AEC＝90°，
∴四边形AECF是矩形．
【点睛】本题考查了矩形的判定、平行四边形的判定与性质等知识；熟练掌握矩形的判定方法，证出四边形AECF为平行四边形是解题的关键．
19. 如图，AD是△ABC的中线，AB：AD：BC＝13：12：10，△ABD的周长是60cm．求AC．

【答案】AC＝26（cm）
【解析】
【分析】设AB＝13x，AD＝12x，BC＝10x，则BD＝CD＝5x，所以13x+12x+5x＝60，解得x＝2，根据勾股定理的逆定理可证明△ABD为直角三角形，∠ADB＝90°，所以AD垂直平分BC，从而得出答案即可.
【详解】设AB＝13x，AD＝12x，BC＝10x，
∵AD是△ABC的中线，
∴BD＝CD＝5x，
∵△ABD的周长是60cm，
∴13x+12x+5x＝60，解得x＝2，
∴BD＝10，AD＝24，AB＝26，
∵102+242＝262，
∴BD2+AD2＝AB2，
∴△ABD为直角三角形，∠ADB＝90°，
∴AD⊥BC，
而BD＝CD，
∴AC＝AB＝26（cm）．
【点睛】本题主要考查了勾股定理逆定理的运用，熟练掌握相关概念是解题关键.
四、解答题（二）（每小题8分，共24分）
20. 已知，求下列各式的值．
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】本题考查了实数的混合运算，平方差公式运算，代数式求值，多项式乘以多项式，熟练掌握运算法则是解题关键．
（1）先算出，的值，再利用平方差公式进行计算代入求值即可；
（2）先求出，的值，再利用多项式乘以多项式进行计算代入求值即可．
【小问1详解】
解：，
，，
【小问2详解】
，
，，
．
21. 如图，在中，，月，求的长和的面积．
【答案】，的面积为
【解析】
【分析】本题考查了勾股定理，垂线性质，直角三角形的两锐角互余，含角的直角三角形特征，等角对等边，过点A作于点D，根据直角三角形的两锐角互余，求出，，再根据含角的直角三角形特征，等角对等边，勾股定理分别求出，的长，再利用勾股定理，以及三角形面积公式求出结果即可．
【详解】解：如图，过点A作于点D，
则，
，
，
，
在中，，
，
，
，
，
在中，，
．
22. 如图，对角线，相交于点，过点作且，连接，，．
（1）求证：是菱形；
（2）若，，求长．
【答案】（1）见解析；
（2）．
【解析】
【分析】本题考查了菱形的判定与性质、平行四边形的判定与性质、矩形的判定与性质、等边三角形的判定与性质以及勾股定理等知识，熟练掌握菱形的判定与性质是解题的关键．
（1）先证四边形是平行四边形，再证平行四边形是矩形，则，得，然后由菱形的判定即可得出结论；
（2）证是等边三角形，得，再由勾股定理得，然后由矩形的在得，，即可解决问题．
【小问1详解】
证明： ，，
四边形是平行四边形．
，
平行四边形是矩形，
，
，
是菱形；
【小问2详解】
解：四边形是菱形，
，，，
，
是等边三角形，
，
，
在中，由勾股定理得：，
由（1）可知，四边形是矩形，
，，
，
即的长为．
五、解答题（三）（每小题10分，共30分）
23. 如图所示，长方形纸片ABCD的长AD＝9cm，宽AB＝3cm，将其折叠，使点D与点B重合．
求：（1）折叠后DE的长；（2）以折痕EF为边的正方形面积．
【答案】（1）DE长为5cm；（2）10cm2
【解析】
【分析】（1）设DE长为xcm，则AE=（9-x）cm，BE=xcm，根据勾股定理得出AE2+AB2=BE2，即（9-x）2+32=x2，解方程求出x，即可得出DE的长；
（2）作EG⊥BC于G，则四边形ABGE是矩形，∠EGF=90°，得出EG=AB=3，BG=AE=4，得出GF=1，由勾股定理求出EF2，即可得出以EF为边的正方形面积．
【详解】（1）设DE长为xcm，则AE=（9-x）cm，BE=xcm，
∵四边形ABCD是矩形，
∴∠A=90°，
根据勾股定理得：AE2+AB2=BE2，
即（9-x）2+32=x2，
解得：x=5，
即DE长为5cm，
（2）作EG⊥BC于G，如图所示：
则四边形ABGE是矩形，∠EGF=90°，
∴EG=AB=3，BG=AE=4，
∴GF=1，
∴EF2=EG2+GF2=32+12=10，
∴以EF为边的正方形面积为EF2=10cm2．
【点睛】本题考查了矩形性质、翻折变换、勾股定理以及正方形的面积；熟练掌握矩形和翻折变换的性质，运用勾股定理进行计算是解决问题的关键．
24. 如图1，四边形是正方形，点是边上任意一点，于点，且交于点．
（1）求证：；
（2）若，，求的长；
（3）如图2，连接、，判断线段与的数量与位置关系，并证明．
【答案】（1）见解析 （2）
（3）DF＝CE，DF⊥CE，证明见解析
【解析】
【分析】（1）先判断出∠AED＝∠BFA＝90°，再判断出∠BAF＝∠ADE，进而利用“角角边”证明△AFB和△DEA全等，即可得出结论；
（2）先根据勾股定理求出AG，再利用面积求出BF，最后用勾股定理即可得出结论；
（3）利用“边角边”证明△FAD和△EDC全等，得出DF＝CE，∠ADF＝∠DCE，即可得出结论．
【小问1详解】
证明：∵DE⊥AG，BFDE，
∴BF⊥AG，
∴∠AED＝∠BFA＝90°，
∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝90°，
∴∠BAF＋∠EAD＝90°，
∵∠EAD＋∠ADE＝90°，
∴∠BAF＝∠ADE，
又∠AED＝∠BFA＝90°，AB＝AD，
∴△AFB≌△DEA（AAS），
∴AF＝DE；
【小问2详解】
解：在Rt△ABG中，AB＝4，BG＝3，根据勾股定理得，AG＝5，
∵AB•BG＝AG•BF，
∴BF＝，
在Rt△ABF中，AF＝；
【小问3详解】
DF＝CE，DF⊥CE．
证明：∵∠FAD＋∠ADE＝90°，∠EDC＋∠ADE＝∠ADC＝90°，
∴∠FAD＝∠EDC，
∵△AFB≌△DEA，
∴AF＝DE，
又∵四边形ABCD是正方形，
∴AD＝CD，
又AF＝DE，∠FAD＝∠EDC，
∴△FAD≌△EDC（SAS），
∴∠ADF＝∠DCE，DF＝CE，
∵∠ADF＋∠CDF＝∠ADC＝90°，
∴∠DCE＋∠CDF＝90°，
∴∠DFC＝90°，即DF⊥CE．
【点睛】此题是四边形综合题，主要考查了正方形的性质，勾股定理，全等三角形的判定和性质，判断出△AFB≌△DEA是解本题的关键．
25. 如图，在Rt△ABC中，∠B＝90°，BC＝，∠C＝30°．点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．
（1）AC的长是 ，AB的长是 ．
（2）在D、E的运动过程中，线段EF与AD的关系是否发生变化？若不变化，那么线段EF与AD是何关系，并给予证明；若变化，请说明理由．
（3）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
【答案】（1）10，5；（2）EF与AD平行且相等，见解析；（3）当t＝时，四边形AEFD为菱形
【解析】
【分析】（1）在Rt△ABC中，∠C＝30°，则AC＝2AB，根据勾股定理得到AC和AB的值．
（2）先证四边形AEFD是平行四边形，从而证得AD∥EF，并且AD＝EF，在运动过程中关系不变．
（3）求得四边形AEFD为平行四边形，进而利用菱形的判定与性质得出AE＝AD时，求出t的值，进而得出答案．
【详解】解：（1）∵在Rt△ABC中，∠C＝30°，
∴AC＝2AB，
根据勾股定理得：AC2﹣AB2＝BC2，
∴3AB2＝75，
∴AB＝5，AC＝10；
（2）EF与AD平行且相等．
在△DFC中，∠DFC＝90°，∠C＝30°，DC＝2t，
∴DF＝t．
又∵AE＝t，
∴AE＝DF，
∵AB⊥BC，DF⊥BC，
∴AE∥DF．
∴四边形AEFD为平行四边形．
∴EF与AD平行且相等．
（3）能，理由如下：
∵AB⊥BC，DF⊥BC，
∴AE∥DF．
又∵AE＝DF，
∴四边形AEFD为平行四边形．
∵AB＝5，AC＝10.
∴AD＝AC﹣DC＝10﹣2t．
若使▱AEFD为菱形，则需AE＝AD，
即t＝10﹣2t，解得：t＝．
即当t＝ 时，四边形AEFD为菱形．
【点睛】本题考查平行四边形、菱形的判定与性质，以及30°角的直角三角形的性质，熟练掌握平行四边形的判定与性质是解题的关键．