山东省滨州市无棣县2023-2024学年八年级下学期期中考试数学试题（原卷版+解析版）

这是一份山东省滨州市无棣县2023-2024学年八年级下学期期中考试数学试题（原卷版+解析版），文件包含山东省滨州市无棣县2023-2024学年八年级下学期期中考试数学试题原卷版docx、山东省滨州市无棣县2023-2024学年八年级下学期期中考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
温馨提示：
1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分，共8页．满分120分．考试用时120分钟．
2．答卷前，考生务必用0.5毫米黑色签字笔将自己的学校、姓名、准考证号填写在答题卡中规定的位置上．
3．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试题卷上．
4. 第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．
第 Ⅰ 卷（选择题 共30分）
一、选择题（本题共10个小题，在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,每小题3分,满分30分）
1. 以下列各组数为边长，能组成直角三角形的是( )｡
A. 8，15，17B. 4，5，6C. 5，8，10D. 8，39，40
【答案】A
【解析】
【详解】试题分析：要组成直角三角形，三条线段满足较小的平方和等于较大的平方即可．
B、42+52≠62，C、52+82≠102， D、82+392≠402，故错误；
A、82+152=172，本选项正确．
考点：本题考查勾股定理的逆定理
点评：解答本题的关键是熟练掌握勾股定理的逆定理：两边的平方和等于第三边的平方，那么这样的三角形是直角三角形．
2. 下列图象中，表示y是x的函数的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据函数的定义逐项进行判定解答即可．
【详解】解：A、每取一个x， y都有唯一的一个值与之对应，所以 y是x的函数，故此选项符合题意；
B、存在一个x值， y有两个值与之对应，所以y不是x的函数，故此选项不符合题意；
C、存在一个x值， y有两个值与之对应，所以y不是x的函数，故此选项不符合题意；
D、存在一个x值， y有两个值与之对应，所以y不是x的函数，故此选项不符合题意；
故选：A．
【点睛】本题主要考查的是函数的概念，掌握在一个变化过程中，有两个变量x、y，若x取一个值，y都有唯一的一个值与之对应，则y是x的函数是解题的关键．
3. 如图，的对角线交于点，下列结论一定成立的是（ ）

A. B. C. D.
【答案】C
【解析】
【分析】根据平行四边形性质逐项验证即可得到答案．
【详解】解：A、根据平行四边形性质：对角线相互平分，在中，，，则不一定成立，该选项不符合题意；
B、根据平行四边形性质：对角线相互平分，不一定垂直，则不一定成立，该选项不符合题意；
C、根据平行四边形性质：对角线相互平分，在中，，该选项符合题意；
D、根据平行四边形性质，对角线不一定平分对角，则不一定成立，该选项不符合题意；
故选：C．
【点睛】本题考查平行四边形性质，熟记平行四边形对角线相互平分是解决问题的关键．
4. 一次函数的图像不经过（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】B
【解析】
【分析】根据一次函数的性质可知一次函数y=x−3的图象经过哪几个象限，不经过哪个象限，从而可以解答本题．
【详解】解：∵一次函数y=x−3中，k=1，b=-3，
∴一次函数的图像经过一、三、四象限，不经过第二象限，
故选B．
【点睛】本题考查一次函数的性质和图象，解答本题的关键是明确题意，利用一次函数的性质解答．
5. 图1是第七届国际数学教育大会（）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形．若，则的值为（ ）

A. B. C. D.
【答案】A
【解析】
【分析】根据题意先求出，再利用勾股定理即可求解．
【详解】解：在中，，，
，
在中，
．
故选：A．
【点睛】本题意考查勾股定理，熟练运用勾股定理求直角三角形的边长是解题关键．
6. 下列命题正确的是（ ）
A. 一组邻边相等的四边形是菱形B. 对角互补的四边形是平行四边形
C. 矩形的对角线互相垂直D. 正方形的对角线相等且互相平分
【答案】D
【解析】
【分析】本题主要考查了判断命题的真假，熟知菱形的判定定理，平行四边形的判定定理，矩形的性质和正方形的性质是解题的关键．
【详解】解：A、一组邻边相等的平行四边形是菱形，原命题是假命题，不符合题意；
B、对角互补的四边形不一定是平行四边边形，例如等腰梯形也满足此条件，原命题是假命题，不符合题意；
C、矩形的对角线不一定互相垂直，原命题是假命题，不符合题意；
D、正方形的对角线相等且互相平分，原命题是假命题，不符合题意；
故选：D．
7. 如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则CD的长为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】利用勾股定理求得相关线段的长度，然后由面积法求得BD的长度，再利用勾股定理即可求出CD的长．
【详解】由勾股定理得：AC==．
∵BC×2=AC•BD，即×2×2=וBD，
∴BD=，
∴CD==．
故选A．
8. 如图，菱形的对角线与相交于点O，E为边的中点，连结．若，则（ ）

A. 2B. C. 3D. 4
【答案】B
【解析】
【分析】先由菱形的性质得，，，再由勾股定理求出，然后由直角 三角形斜边的中线等于斜边的一半求解．
【详解】解：∵菱形，
∴，，，
∴由勾股定理，得，
∵E为边的中点，
∴
故选：B．
【点睛】本考查菱形的性质，勾股定理，直角三角形的性质，熟练掌握菱形的性质，直角三角形的性质是解题的关键．
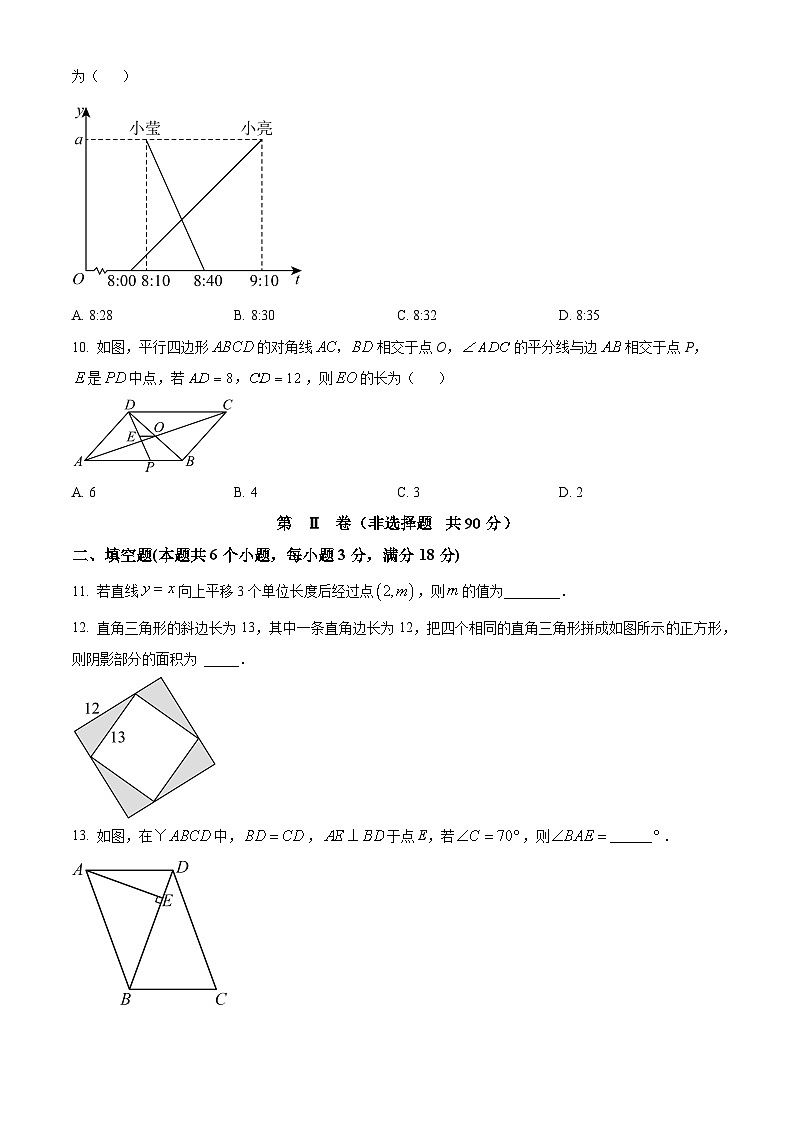
9. 甲乙两地相距a千米，小亮8:00乘慢车从甲地去乙地，10分钟后小莹乘快车从乙地赶往甲地．两人分别距甲地的距离y（千米）与两人行驶时刻t（×时×分）的函数图象如图所示，则小亮与小莹相遇的时刻为（ ）

A. 8:28B. 8:30C. 8:32D. 8:35
【答案】A
【解析】
【分析】利用待定系数法求出两条直线的函数解析式，将两个解析式联立，通过解方程求出交点的横坐标即可．
【详解】解：令小亮出发时对应的t值为0，小莹出发时对应的t值为10，则小亮到达乙地时对应的t值为70，小莹到达甲地时对应的t值为40，
设小亮对应函数图象的解析式为，
将代入解析式得，解得，
小亮对应函数图象的解析式为，
设小莹对应函数图象的解析式为，
将，代入解析式，得，
解得，
小莹对应函数图象的解析式为，
令，得，
解得，
小亮与小莹相遇的时刻为8:28．
故选A．
【点睛】本题考查一次函数的实际应用，解题的关键是利用待定系数法求出两条直线的函数解析式，熟练运用数形结合思想．
10. 如图，平行四边形的对角线相交于点O，的平分线与边相交于点P，是中点，若，则的长为（ ）
A. 6B. 4C. 3D. 2
【答案】D
【解析】
【分析】本题主要考查了平行四边形的性质，三角形中位线定理，角平分线的定义，等角对等边，根据平行四边形的性质可得，再根据平分，可得，从而可得，可得，进一步可得，再根据三角形中位线定理可得，即可求出的长．
【详解】解：∵在平行四边形中，，
∴，
∵平分，
∴，
∴，
∴，
∵，
∴，
∵E是中点，
∴．
故答案为：2．
第 Ⅱ 卷（非选择题 共90分）
二、填空题(本题共6个小题，每小题3分，满分18分)
11. 若直线向上平移3个单位长度后经过点，则的值为________．
【答案】5
【解析】
【分析】根据平移的规律求出平移后的解析式，再将点代入即可求得的值．
【详解】解：直线向上平移3个单位长度，
平移后的直线解析式为：．
平移后经过，
．
故答案为：5．
【点睛】本题考查的是一次函数的平移，解题的关键在于掌握平移的规律：左加右减，上加下减．
12. 直角三角形的斜边长为13，其中一条直角边长为12，把四个相同的直角三角形拼成如图所示的正方形，则阴影部分的面积为 _____．

【答案】120
【解析】
【分析】根据勾股定理求出的长度，再根据三角形的面积公式求出的面积，即可求出阴影部分面积．
【详解】解：在中，，
∴，
∴阴影部分的面积．
故答案是：120．
【点睛】本题主要考查了勾股定理，解题的关键是掌握直角三角形两直角边平方和等于斜边平方．
13. 如图，在中，，于点E，若，则______．

【答案】
【解析】
【分析】证明，，由，可得，结合，可得．
【详解】解：∵，，
∴，，
∵，
∴，
∴，
∵，
∴；
故答案为：
【点睛】本题考查的是等腰三角形的性质，平行四边形的性质，三角形的内角和定理的应用，熟记基本几何图形的性质是解本题的关键．
14. 如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=1，则边BC的长为_____．
【答案】3
【解析】
【分析】根据翻折变换的特点可知．
【详解】解：根据翻折变换的特点可知：DE=GE
∵∠CFE=60°，
∴∠GAE=30°，
∴AE=2GE=2DE=2，
∴AD=3，
∴BC=3．
故答案为3．
【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
15. 如图，根据函数图象回答问题：方程组的解为______．

【答案】
【解析】
【分析】首先观察函数的图象经过点，然后求得值确定函数的解析式，最后求得两图象的交点求方程组的解即可．
【详解】解：根据图象知：经过点，
所以，
解得：，
所以解析式为，
当时，，
所以两个函数图象均经过
所以方程组的解为，
故答案为：．
【点睛】此题主要考查一次函数与二元一次方程组，关键是能根据函数图象的交点解方程组．
16. 如图①，在矩形ABCD中，动点P从A出发，以相同的速度，沿A→B→C→D→A方向运动到点A处停止．设点P运动的路程为x，△PAB面积为y，如果y与x的函数图象如图②所示，则矩形ABCD的面积为__．

【答案】24
【解析】
【分析】根据图象②得出AB、BC的长度，再求出面积即可．
【详解】解：从图象②和已知可知：AB=4，BC=10-4=6，
所以矩形ABCD的面积是4×6=24，
故答案为24．
【点睛】本题考查了矩形的性质和函数图象，能根据图形得出正确信息是解此题的关键．
三．解答题（共计72分）
17. 如图，直线l是一次函数的图象．
（1）求出这个一次函数的解析式．
（2）根据函数图象，直接写出时x的取值范围．
【答案】（1）
（2）
【解析】
【分析】（1）根据图形确定出一次函数图象上两点坐标，代入解析式求出k与b的值，即可求出解析式；
（2）根据图象确定出x的范围即可．
【小问1详解】
解：将点、分别代入，
得：，
解得，
所以，该一次函数解析式为：；
【小问2详解】
由图象可知，
当时x的取值范围是：．
【点睛】此题考查了待定系数法求一次函数解析式，一次函数图象与性质，熟练掌握待定系数法是解本题的关键．
18. 如图，在▱ABCD中，∠BAD的平分线AE交DC于E，∠DAE＝25°．
（1）求∠C，∠B的度数；
（2）若BC＝5，AB＝8，求CE的长．
【答案】（1）∠C＝50°，∠B＝130°；（2）EC＝3
【解析】
【分析】（1）先由角平分线的定义求出∠DAB＝50°，然后根据平行四边形的性质求解即可；
（2）通过证明∠DAE＝∠DEA，得到DE＝AD=5，然后可求CE的值；
【详解】解：（1）∵∠BAD的平分线AE交DC于E，∠DAE＝25°，
∴∠DAB＝2∠DAE＝50°，
∵四边形ABCD是平行四边形，
∴∠C＝∠DAB＝50°，∠B＝180°﹣50°＝130°；
（2）∵∠BAD平分线AE交DC于E，
∴∠BAE=∠DAE，
∵四边形ABCD平行四边形，
∴ABCD，AD=BC=5，CD=AB=8，
∴∠BAE=∠DEA，
∴∠DAE＝∠DEA，
∴DE＝AD=5
∴CE＝CD﹣DE＝8﹣5＝3，
【点睛】本题考查了角平分线定义，等腰三角形的判定，以及平行四边形的性质，熟练掌握平行四边行的性质是解答本题的关键．平行四边形的性质有：平行四边形对边平行且相等；平行四边形对角相等，邻角互补；平行四边形的对角线互相平分．
19. 如图，．
（1）尺规作图：作的垂直平分线交于点D，交于点E（不写作法，保留作图痕迹）；
（2）在（1）的基础上，连接，求的长．
【答案】（1）见解析；
（2）BD=5．
【解析】
【分析】（1）依据几何语言进行作图即可得到AB的垂直平分线DE；
（2），设BD=x，则AD=x，CD=8-x，依据勾股定理可得Rt△BCD中，BC2+CD2=BD2，解方程即可得到BD的长．
【小问1详解】
如图1，所作直线DE即为线段AB的垂直平分线，
【小问2详解】
解：如图，
∵DE垂直平分AB，
∴AD=BD，
设BD=x，则AD=x，CD=8-x，
∵Rt△BCD中，BC2+CD2=BD2，
∴42+（8-x）2=x2，
解得x=5，
∴BD=5．
【点睛】本题主要考查了基本作图以及线段垂直平分线的性质的运用，线段垂直平分线上任意一点，到线段两端点的距离相等．
20. 为了绿化环境，我县某中学有一块四边形的空地，如图所示，经测量，．

（1）求出空地的面积．
（2）若每种植1平方米草皮需要200元，问总共需投入多少元？
【答案】（1）36平方米
（2）7200元
【解析】
【分析】本题考查勾股定理及逆定理的应用．
（1）连接，在直角三角形中，利用勾股定理求出，再利用勾股定理的逆定理判断得到三角形为直角三角形，四边形面积等于三角形面积+三角形面积，求出即可；
（2）由（1）求出的面积，乘以200即可得到结果．
【小问1详解】
解：连接，

在中，，
在中，，
而，
即，
∴，
则
【小问2详解】
所需费用（元）．
21. 如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD．
（1）求证：四边形OCED菱形；
（2）连接AE、BE，AE与BE相等吗？请说明理由．
【答案】（1）证明见解析；（2）AE=BE，理由见解析．
【解析】
【分析】（1）先判断四边形OCDE是平行四边形，又因为四边形ABCD是矩形，两个结论联合起来，可知四边形OCDE是菱形；
（2）先证出∠ADE=∠BCE，再证明△ADE≌△BCE，从而得出AE=BE．
【详解】解：（1）四边形OCDE是菱形．理由如下：
∵DE∥AC，CE∥BD，
∴四边形OCDE是平行四边形，
∵矩形ABCD的对角线AC、BD相交于点O，
∴OC=AC=BD=OD，
∴四边形OCDE是菱形；
（2）AE=BE，理由是：
∵四边形ABCD是矩形，
∴AD=BC，∠ADC=∠BCD，
∵四边形OCDE是菱形，
∴ED=EC，∠EDC=∠ECD，
∴∠EDC+∠ADC =∠ECD+∠BCD，
即∠ADE =∠BCE
在△ADE和△BCE中，
∵，
∴△ADE≌△BCE，
∴AE=BE．
22. 如图，在正方形ABCD中，点E是BC上的点，DF⊥AE于点F，BG⊥AE于点G．
（1）猜想AG、BG、FG的关系并证明；
（2）若正方形ABCD边长为m，∠BAE=30°，求FG的长（用含m的式子表示）．
【答案】（1），证明见解析
（2）
【解析】
【分析】（1）由正方形的性质结合题意，利用“AAS”易证△BAG≌△DAF，即得出BG=AF，从而可证明；
（2）由题意知，根据含30°角的直角三角形的性质可求出，再根据勾股定理即可求出，从而即可求出FG的长．
【小问1详解】
猜想：.
证明：∵四边形ABCD是正方形，
∴AB=AD，∠DAB=90°．
∵DF⊥AE，BG⊥AE
∴∠AFD=∠BGA=90°，
∴，
∴∠ABG=∠FAD，
∴△BAG≌△DAF(AAS)
∴BG=AF．
∵
∴；
【小问2详解】
由题意知，
在中，，则
由勾股定理得，
∴．
【点睛】本题考查正方形的性质，三角形全等的判定和性质，含30°角的直角三角形的性质以及勾股定理．利用数形结合的思想是解题关键．
23. 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．
（1）求当x≥20时y与x的函数关系式；
（2）若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．
【答案】（1）y＝6.4x+32；（2）B种树苗35棵，总费用最低，最低326元
【解析】
【分析】（1）根据函数图象找出点的坐标，结合点的坐标分段利用待定系数法求出函数解析式即可；
（2）根据B种苗的数量不超过35棵，但不少于A种苗的数量可得出关于x的一元一次不等式组，解不等式组求出x的取值范围，再根据“所需费用为W＝A种树苗的费用＋B种树苗的费用”可得出W关于x的函数关系式，根据一次函数的性质即可解决最值问题．
【详解】解：（1）当x≥20时，设y与x的函数关系式为：y＝kx+b，
把（20，160），（40，288）代入y＝kx+b得：
，
解得：
∴当x≥20时，y与x的函数关系式为y＝6.4x+32；
（2）∵B种苗的数量不超过35棵，但不少于A种苗的数量，
∴
∴22.5≤x≤35
设总费用为W元，则W＝6.4x+32+7（45﹣x）＝﹣0.6x+347
∵k＝﹣0.6，
∴y随x的增大而减小
∴当x＝35时，W总费用最低，W最低＝﹣0.6×35+347＝326（元）．
【点睛】本题考查了一次函数的应用、待定系数法求函数解析式以及解一元一次不等式组，解题的关键是：（1）分段，利用待定系数法求出函数解析式；（2）根据数量关系找出W关于x的函数关系式．本题属于中档题，难度不大，解决该题型题目时，根据函数图象找出点的坐标，再利用待定系数法求出函数解析式是关键．
24. 【背景介绍】
勾股定理是几何学中的明珠，充满着魅力，千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者，向常春在1994年构造发现了一个新的证法．如图．
【小试牛刀】
把两个全等的直角三角形如图1放置，其三边长分别为，，．显然，，．请用，，分别表示出梯形，四边形，的面积，再探究这三个图形面积之间的关系，可得到勾股定理：__________，__________，__________，则它们满足的关系式为__________，经化简，可得到勾股定理．
【知识运用】
如图2，河道上，两点（看作直线上的两点）相距160米，，为两个菜园（看作两个点），，，垂足分别为，，米，米，现在菜农要在上确定一个抽水点，使得抽水点到两个菜园，的距离和最短，则该最短距离为__________米．
【知识迁移】
借助上面的思考过程，画图说明并求代数式的最小值．
【答案】（小试牛刀），，， ；（知识运用）200；（知识迁移）15
【解析】
【分析】（小试牛刀）根据梯形、三角形的面积公式求解即可；
（知识运用）作点关于的对称点，连接，则，由三角形三边关系可得当三点共线时，距离最小；
（知识迁移）如下图，，，、，点为线段上一点，则，由上可得当三点共线时，距离最小．
【详解】解：（小试牛刀）；
；
，
满足的关系式为：．
（知识运用）作点关于的对称点，连接，如下图：
由题意可得：，
，则的最小值，即为的最小值，
由三角形三边关系可得：，当三点共线时，
∴的最小值为，
作交延长线于点F，
∵，
∴四边形是矩形，
∴，，
∴米，
故答案为：；
（知识迁移）如下图，，，、，点为线段上一点，
设，则，
∴，
由上可得当三点共线时，距离最小，最小为，
作交延长线于点F，
∵，
∴四边形是矩形，
∴，，
∴．
∴代数式的最小值为15．
【点睛】此题考查了勾股定理的证明以及勾股定理的应用，解题的关键是熟练掌握勾股定理的应用．