数学七年级下册2 三角形的外角和与外角和多媒体教学ppt课件

这是一份数学七年级下册2 三角形的外角和与外角和多媒体教学ppt课件，共14页。PPT课件主要包含了学习目标，重难点，情景导入，教学过程，探究新知，例题精讲等内容，欢迎下载使用。
1.掌握三角形的内角和及外角的性质.2.运用三角形相关性质解决问题.
重点：掌握三角形的内角和以及三角形外角的性质以及其外角的和.难点：在三角形外角的性质证明的过程中，涉及到添加辅助线来沟通证明思路的方法.
在小学我们曾剪下三角形的两个内角，将它们与第三个内角拼在一起，发现三个内角恰好拼成一个平角，于是我们得出如下结论：三角形的内角和等于180°.现在我们尝试用说理的方式来说明三角形的内角和是180°.如图，已知△ABC，分别用∠1、∠2、∠3表示△ABC 的三个内角，证明∠1+∠2+∠3=180°.
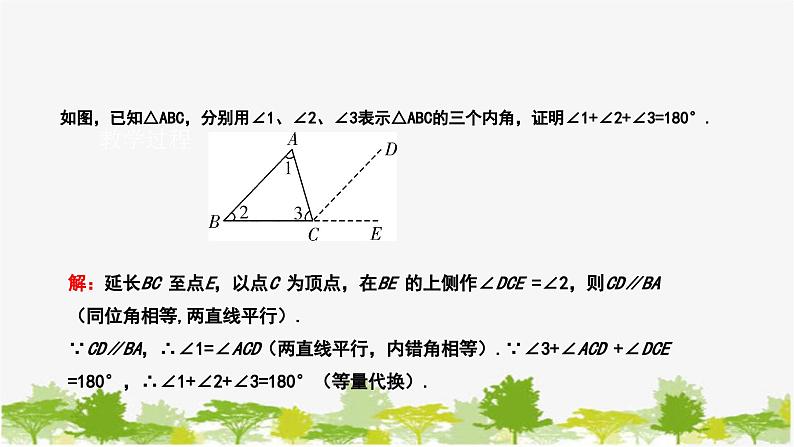
如图，已知△ABC，分别用∠1、∠2、∠3表示△ABC的三个内角，证明∠1+∠2+∠3=180°.
解：延长BC 至点E，以点C 为顶点，在BE 的上侧作∠DCE =∠2，则CD∥BA（同位角相等,两直线平行）.∵CD∥BA，∴∠1=∠ACD（两直线平行，内错角相等）.∵∠3+∠ACD +∠DCE =180°，∴∠1+∠2+∠3=180°（等量代换）.
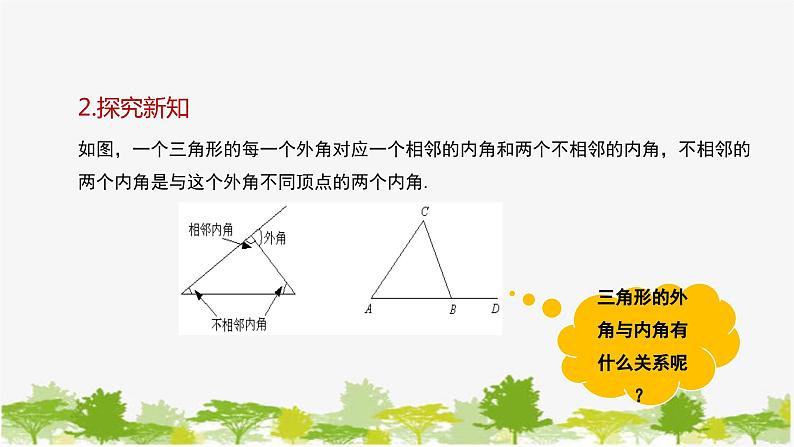
如图，一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角，不相邻的两个内角是与这个外角不同顶点的两个内角.
三角形的外角与内角有什么关系呢？
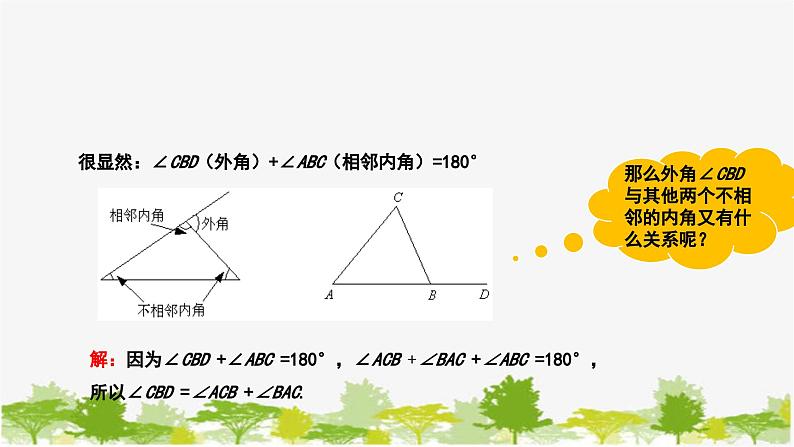
很显然：∠CBD（外角）+∠ABC（相邻内角）=180°
解：因为∠CBD +∠ABC =180°，∠ACB +∠BAC +∠ABC =180°，所以∠CBD =∠ACB +∠BAC.
那么外角∠CBD与其他两个不相邻的内角又有什么关系呢？
由此可知，三角形的外角有两条性质：(1)三角形的一个外角等于和它不相邻的两个内角的和；(2)三角形的一个外角大于任何一个与它不相邻的内角.
问题2：你能用“三角形的内角和等于180°”来说明图中∠1+∠2+∠3=360°吗？
解：因为∠1＋∠ACB ＝∠2＋∠BAC ＝∠3＋∠ABC ＝180°，所以∠1＋∠2＋∠3＋∠ACB ＋∠ABC ＋∠BAC ＝180°×3.又因为∠ACB＋∠BAC＋∠ABC＝180°，所以∠1＋∠2＋∠3＝180°×3-180°＝360°
结论:三角形的外角和等于360°.
【知识归纳】（1）三角形的内角和等于180°.（2）直角三角形的两个锐角互余 .（3）三角形外角的两条性质： 三角形的一个外角等于与它不相邻的两个内角的和； 三角形的一个外角大于任何一个与它不相邻的内角.（4）三角形的外角和等于360°.
例1 如图D 是△ABC 的BC 边上一点，∠B ＝∠BAD，∠ADC ＝80°，∠BAC ＝70°.求：(1)∠B 的度数； (2)∠C 的度数.
解：(1)因为∠ADC 是△ABD 的外角，所以∠ADC ＝∠B ＋∠BAD ＝80°.又因为∠B ＝∠BAD,所以∠B ＝80°÷2＝40°；(2)在△ABC 中，因为∠B ＋∠BAC ＋∠C ＝180°，所以∠C ＝180°－∠B－∠BAC ＝180°－40°－70°＝70°.
例2 如图，AD∥BC，你能说明∠1＋∠2＋∠3＝360°吗？
解：因为AD∥BC，所以∠EAD＝∠1，∠DAB＝∠3，所以∠1＋∠2＋∠3＝∠EAD＋∠2＋∠DAB＝360°.
4.巩固练习 完成教材课后同步练习