





- 数学(盐城卷)-2024年中考数学考前押题卷 试卷 1 次下载
- 数学(苏州卷)-2024年中考数学考前押题卷 试卷 1 次下载
- 数学(重庆卷)-2024年中考数学考前押题卷 试卷 2 次下载
- 数学(四川成都卷)-2024年中考数学考前押题卷 试卷 1 次下载
- 数学(上海卷)-2024年中考数学考前押题卷 试卷 4 次下载
数学(浙江卷)-2024年中考数学考前押题卷
展开第Ⅰ卷
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
第Ⅱ卷
二、填空题(本大题共6小题,每小题4分,共24分)
11.3xy(2y﹣x) 12.20 13.45
14. 15. 16. 3
三、解答题(本大题共8个小题,共66分.解答应写出文字说明,证明过程或演算步骤)
17.(6分)【解析】解:(1)上面第二步计算中,中括号里的变形是通分,通分的依据是分式的基本性质,
故答案为:通分;(1分)
(2)第三步出现错误,原因是分子相减时未变号,
原式=[﹣]×,
=[﹣]×,
=×,
=×,(3分)
=.(4分)
故答案为:三.
(3)当x=0时,上式==.(6分)
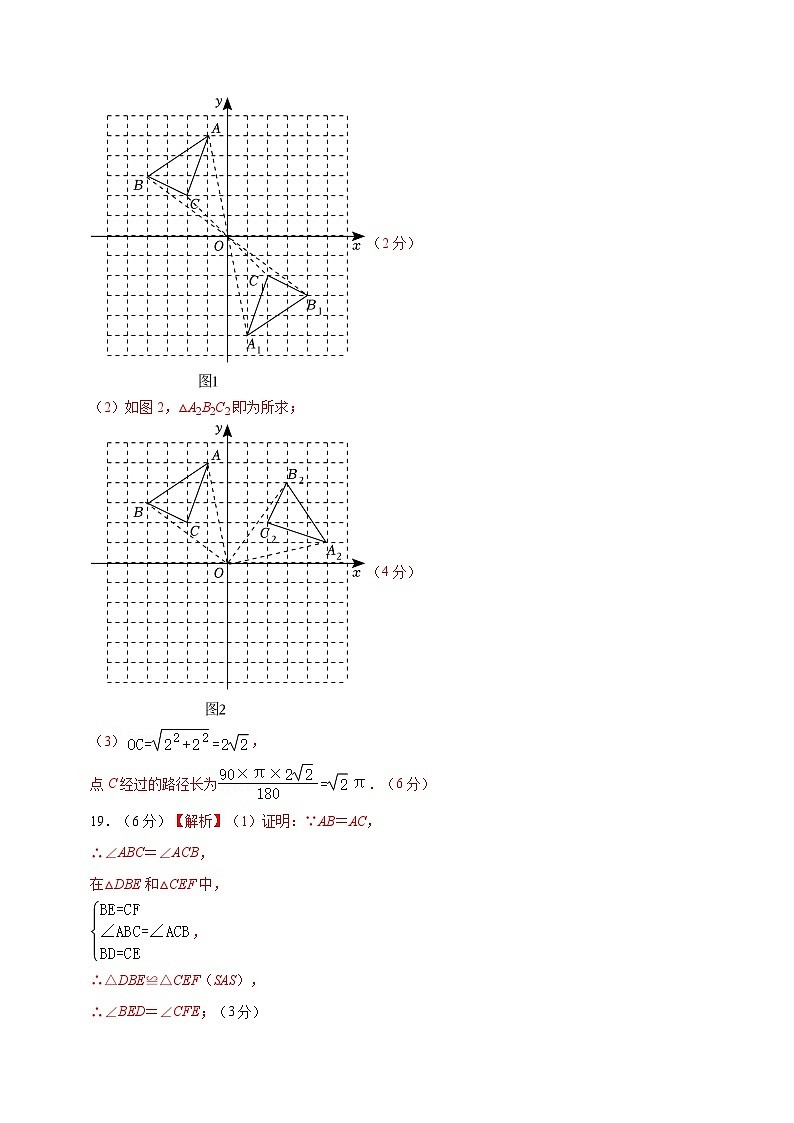
18.(6分)【解析】解:(1)如图1,△A1B1C1即为所求.A1(1,﹣5),B1(4,﹣3),C1(2,﹣2);
(2分)
(2)如图2,△A2B2C2即为所求;
(4分)
(3),
点C经过的路径长为.(6分)
19.(6分)【解析】(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△CEF中,
,
∴△DBE≌△CEF(SAS),
∴∠BED=∠CFE;(3分)
(2)解:由(1)知:△DBE≌△CEF,
∴∠1=∠3,
∵∠A+∠B+∠C=180°,∠B=∠C,
∴∠B=(180°﹣44°)=68°,
∴∠1+∠2=180°﹣68°=112°,
∴∠3+∠2=112°,
∴∠DEF=180°﹣112°=68°.(6分)
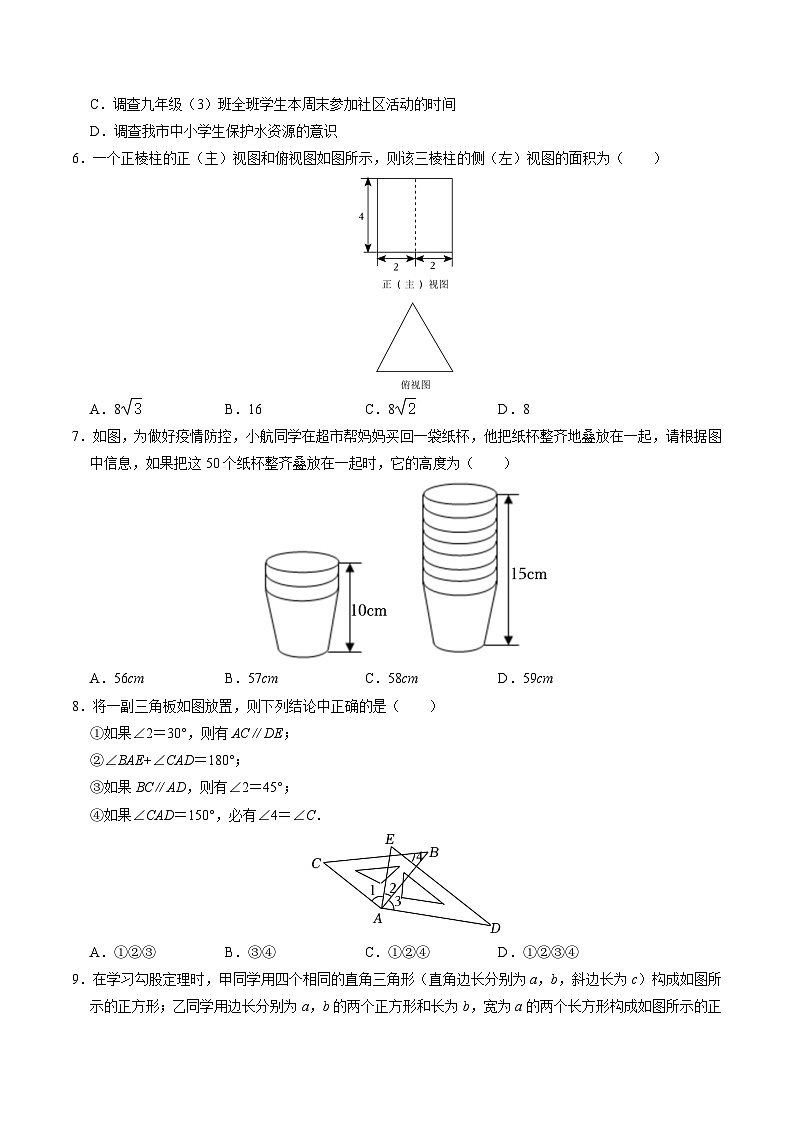
20.(8分)【解析】解:(1)在被抽取20名八年级学生进行1分钟跳绳测试成绩中,165出现的次数最多,故众数a=165;
把被抽取20名八年级学生进行1分钟跳绳测试成绩从小到大排列,排在中间的两个数分别是148,152,故中位数b==150.
故答案为:165;150;(3分)
(2)500×=175(名),
答:估计八年级500名学生中,约有175名学生能达到优秀;(5分)
(3)超过年级一半的学生,理由如下:
∵152>150,
∴推测该同学的1分钟跳绳次数超过年级一半的学生.(8分)
21.(8分)【解析】解:(1)由图可得,甲车的速度为120÷2=60(km/h),
故答案为:60;(2分)
(2)∵乙车从B地以80km/h的速度匀速驶往A地,两车同时到达目的地,
∴乙车行驶时间为120÷80=1.5(h),
∵2﹣1.5=0.5(h),
∴乙车比甲车晚出发0.5h,
画出y2与x的函数图象如下:
图象CD即为y2与x的函数图象,
由题意得y1=60x,
设CD的函数表达式为y2=﹣80x+b,将(2,0)代入y2=﹣80x+b,得b=160,
∴y2=﹣80x+160,(3分)
由﹣80x+160=60x,解得x=,
∴甲车出发后h与乙车相遇,
答:甲车出发后h与乙车相遇;(5分)
(3)根据题意得y1=60x,y2=120﹣80(x﹣m)=﹣80x+120+80m,
由60x=﹣80x+120+80m得:x=+m,
当x=+m时,y1=y2=60(+m),
∵甲、乙两车在距A地60km至72km之间的某处相遇,
∴60<60(+m)<72,
解得<m<,
∴m的范围是<m<.(8分)
22.(10分)【解析】解:任务1:设OA段h关于s的函数解析式为h=ks,
∴k==tan45°=1,
∴h=s,
∴当h=4时,s=4,
∴OA段h关于s的函数解析式为h=s(0≤s≤4);(1分)
2号机从O点到达A点飞行的路程为OA==4(km),所用时间为min,
∴2号机的爬升速度为4÷=3(km/min).(3分)
任务2:B点的横坐标为4+1×3=7,
∴B点的坐标为(7,4).
设BC段h关于s的函数解析式为h=k1s+b(k1、b为常数,且k1≠0).
将坐标B(7,4)和C(10,3)分别代入h=k1s+b,
得,解得,
∴BC段h关于s的函数解析式为h=﹣s+.(5分)
当h=0时,0=﹣s+,解得s=19,
∴预计2号机着陆点的坐标为(19,0).(6分)
任务3:当2号机在OA段,且PQ=3时,5﹣s=3,解得s=2;
当2号机在BC段,且PQ=3时,5﹣(﹣s+)=3,解得s=13,(8分)
根据图象可知,当2≤s≤13时,两机距离PQ不超过3km,
∴两机距离PQ不超过3km的时长是(13﹣2)÷3=(min).(10分)
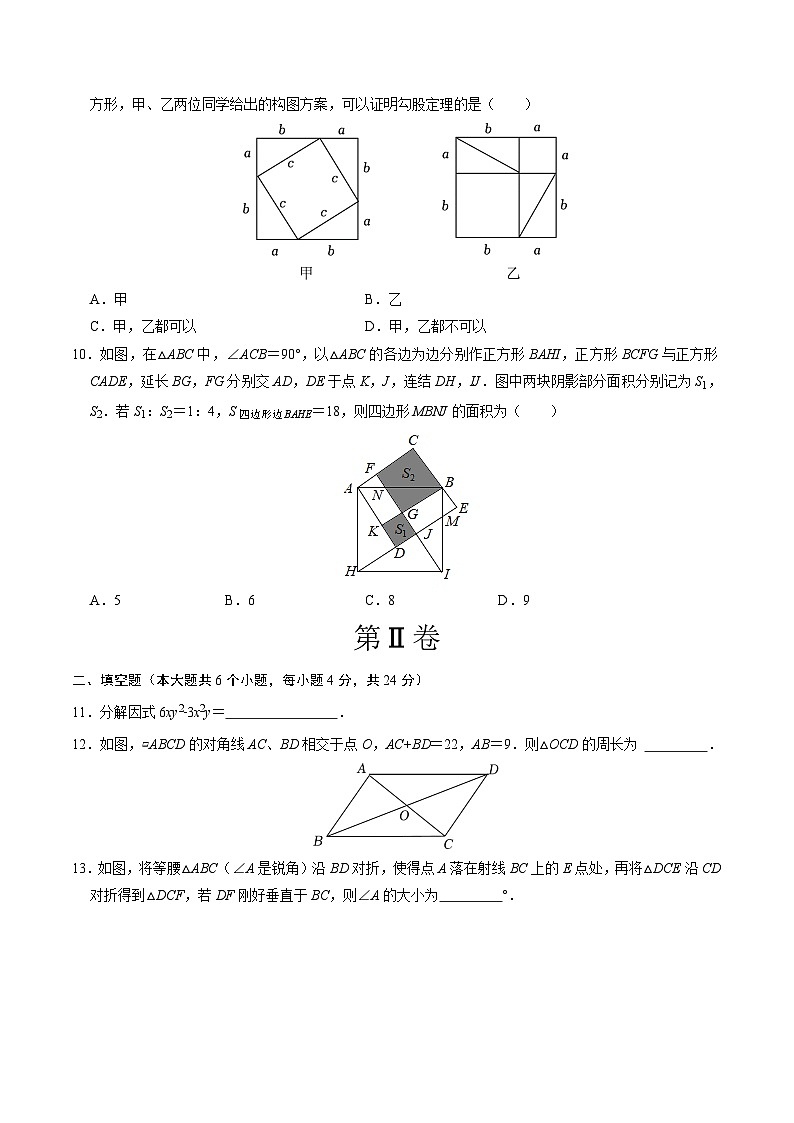
23.(10分)【解析】(1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转的性质得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°﹣45°=45°,
∴∠MAN=∠EAN,
在△AMN和△AEN中,
,
∴△AMN≌△AEN(SAS),(1分)
∴MN=EN,
∵EN=BE+BN=DM+BN,
∴MN=BN+DM,
在Rt△CMN中,由勾股定理得:MN===10,
则BN+DM=10,
设正方形ABCD的边长为x,则BN=BC﹣CN=x﹣6,DM=CD﹣CM=x﹣8,
∴x﹣6+x﹣8=10,
解得:x=12,
即正方形ABCD的边长是12;
故答案为:12;(3分)
(2)证明:设BN=m,DM=n,
由(1)可知,MN=BN+DM=m+n,
∵∠B=90°,tan∠BAN=,
∴tan∠BAN==,
∴AB=3BN=3m,
∴CN=BC﹣BN=2m,CM=CD﹣DM=3m﹣n,
在Rt△CMN中,由勾股定理得:(2m)2+(3m﹣n)2=(m+n)2,
整理得:3m=2n,(4分)
∴CM=2n﹣n=n,
∴DM=CM,
即M是CD的中点;(6分)
(3)解:延长AB至P,使BP=BN=4,过P作BC的平行线交DC的延长线于Q,延长AN交PQ于E,连接EM,如图③所示:
则四边形APQD是正方形,
∴PQ=DQ=AP=AB+BP=12+4=16,
设DM=a,则MQ=16﹣a,
∵PQ∥BC,
∴△ABN∽△APE,
∴===,
∴PE=BN=,
∴EQ=PQ﹣PE=16﹣=,(8分)
由(1)得:EM=PE+DM=+a,
在Rt△QEM中,由勾股定理得:()2+(16﹣a)2=(+a)2,
解得:a=8,
即DM的长是8;
故答案为:8.(10分)
24.(12分)【解析】解:(1)连接AC,CE,
∵A(﹣1,0)、E(1,0),
∴OA=OE=1,
∵OC⊥AE,
∴AC=CE,
∵AE=CE,
∴AC=CE=AE,(2分)
∴∠CAE=60°,
∴∠BEC=2∠CAB=120°,
∴的度数为120°,
故答案为:120;(3分)
(2)由题可得,AB为⊙E直径,且AB⊥CD,
由垂径定理可得,CO=OD,
连接PD,如图2,
又∵G为PC的中点,
∴OG∥PD,且OG=,
当D,E,P三点共线时,此时DP取得最大值,(5分)
且DP=AB=2AE=4,
∴OG的最大值为2,
故答案为:2;(7分)
(3)连接AC,BC,
∵直径AB⊥CD,
∴,
∴∠ACD=∠CPA,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
∴∠ACD+∠DCQ=∠CPA+∠PCQ,
∴∠ACQ=∠AQC,
∴AQ=AC,
∵∠CAO=60°,AO=1,
∴AC=2,
∴AQ=2;
(4)由题可得,直径AB⊥CD,
∴AB垂直平分CD,
如图4,连接AC,AD,则AC=AD,
由(1)得,∠DAC=120°,
将△ACP绕A点顺时针旋转120°至△ADM,
∴△ACP≌△ADM,
∴∠ACP=∠ADM,PC=DM,
∵四边形ACPD为圆内接四边形,
∴∠ACP+∠ADP=180°,
∴∠ADM+∠ADP=180°,
∴M、D、P三点共线,(8分)
∴PD+PC=PD+DM=PM,
过A作 AG⊥PM于G,则 PM=2PG,
⋅∠APM=∠ACD=30°,
在 Rt△APG 中,∠APM=30°,(10分)
设AG=x,则AP=2x,
∴,
∴
∴,
∴
∴ 为定值.(12分)
1
2
3
4
5
6
7
8
9
10
C
B
B
A
C
A
B
D
A
B
数学(徐州卷)-2024年中考数学考前押题卷: 这是一份数学(徐州卷)-2024年中考数学考前押题卷,文件包含数学徐州卷全解全析docx、数学徐州卷参考答案及评分标准docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
数学(南京卷)-2024年中考数学考前押题卷: 这是一份数学(南京卷)-2024年中考数学考前押题卷,文件包含数学南京卷全解全析docx、数学南京卷参考答案及评分标准docx、数学南京卷考试版A4docx等3份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
2024年中考考前最后一套押题卷:数学(浙江卷)(考试版)A4: 这是一份2024年中考考前最后一套押题卷:数学(浙江卷)(考试版)A4,共6页。试卷主要包含了第1组数据为等内容,欢迎下载使用。












