数学（四川成都卷）-2024年中考数学考前押题卷

这是一份数学（四川成都卷）-2024年中考数学考前押题卷，文件包含数学四川成都卷全解全析docx、数学四川成都卷参考答案及评分标准docx、数学四川成都卷考试版A4docx等3份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

A卷
一、选择题（本大题共8个小题，每小题4分，共32分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
二、填空题（本大题共5小题，每小题4分，共20分）
9．
10．－5
11．6
12．6
13．56
三、解答题（本大题共5个小题，共48分．解答应写出文字说明，证明过程或演算步骤）
14．（12分）【详解】原式
；（6分）
解不等式，得：，
解不等式，得：，
则不等式组的解集为，（10分）
将解集表示在数轴上如下：
（12分）
15．（8分）【详解】解：如图：
设，
由题意得：，
∴，
∴，（2分）
由题意得：，，，
∴，（4分）
在中，，∴，
∵，
∴，解得：，（6分）
∴，
∴，（8分）
∴该古塔的高度约为．
16．（8分）【详解】（1）解：名，
∴本次调查的学生人数为120名，即样本容量为120，
∴，，
故答案为：120，12，36；（4分）
（2）解：类别的人数为：（人）
补全条形统计图如图所示：

类别所占的百分比为：，（人）（6分）
∴全校喜爱“葫芦雕刻”的学生人数约为625人．
（3）解：画树状图如下：
由树状图可知一共有6种等可能性的结果数，其中恰好选到一名男生和一名女生的结果数有4种，
∴恰好选到一名男生和一名女生的概率．（8分）
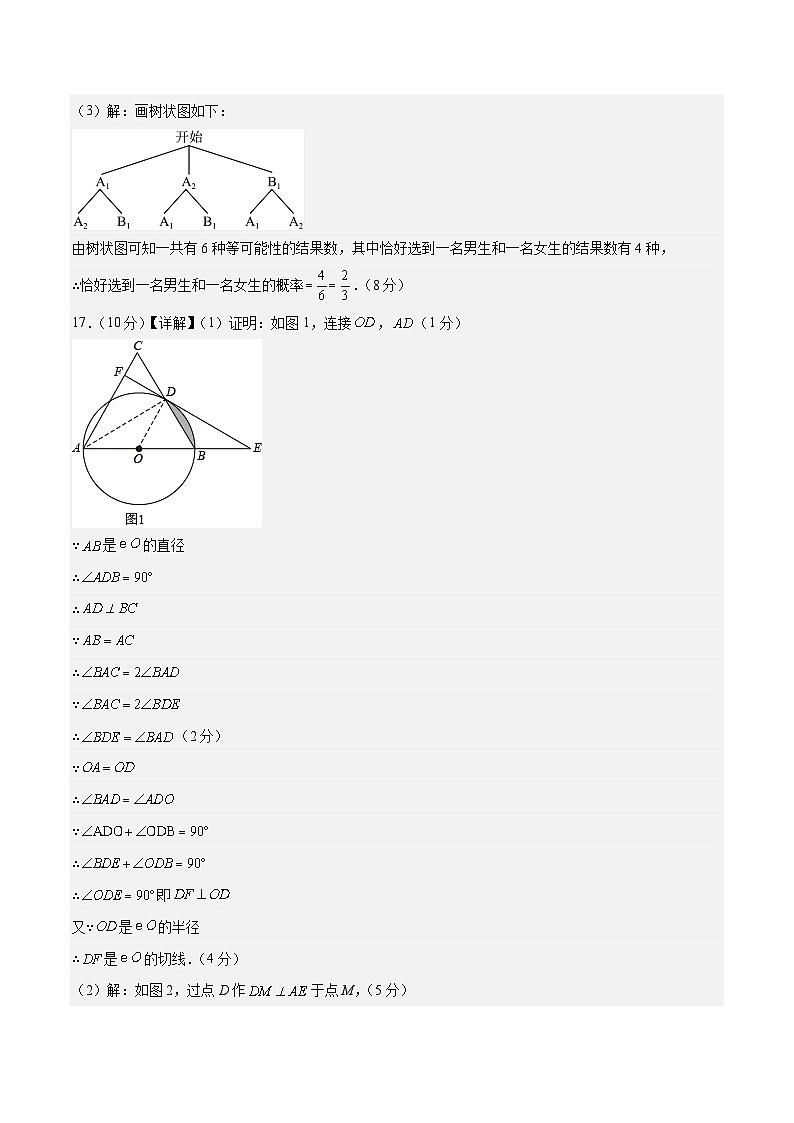
17．（10分）【详解】（1）证明：如图1，连接，（1分）
∵是的直径
∴
∴
∵
∴
∵
∴（2分）
∵
∴
∵
∴
∴即
又∵是的半径
∴是的切线．（4分）
（2）解：如图2，过点D作于点M，（5分）
∵
∴
∵
∴是的中位线
∴
∵
∴
∵
∴
∴和为等边三角形（7分）
在中，
∴
∴
∴
在中，
∴，（8分）
∵，
（10分）
∴阴影部分的面积为．
18．（10分）【详解】（1）解：∵、均在反比例函数的图象上，
∴，
解得，，
∴反比例函数表达式为；（2分）
（2）如图，连接，
∵为菱形，
∴，
∵，点C为的中点，
，
∴，
∴，
∴，
∴，（3分）
令，
∵，
∴，
又∵，
∴(舍)，
∴，
在中，，
∴，
∵，
∴，
又∵点P是反比例函数图象上一点，
∴点P的坐标为．（5分）
（3）过点F作轴于点G，与x轴交于点T，
设点，点F坐标为，
则，
∵四边形是平行四边形，
∴，
∵,
∴，
又∵，
∴，（7分）
∴，∴，
∴，解得，
∵a，b异号，，∴，
∴，
由（1）知，
∴，为定值．（10分）
B卷
一、填空题（本大题共5个小題，每小題4分，共20分，答案写在答题卡上）
19．2021
20．
21．5
22．18
23．5
二、解答题（本大题共3个小题，共30分．解答应写出文字说明，证明过程或演算步骤）
24．（8分）【详解】（）今年型车每辆售价为元，由题意得：
，
解得：，
经检验，是方程的解，且符合题意．
（元），
答：今年型车每辆售价为元；（3分）
（）设经销商新进型车辆，则型车为辆，获利元．由题意得：，
即，（5分）
型车的进货数量不超过型车数量的倍，
，
，
由与的关系式可知，，的值随的值增大而减小．
时，的值最大，最大利润为元．（7分）
（辆），
当经销商新进型车辆，型车辆时，获利最多，最大利润为元．（8分）
答：当经销商新进型车辆，型车辆时，获利最多，最大利润为元．
25．（10分）【详解】（1）矩形OABC，
OC=AB，
A(2，0)，C(0，3)，
OA=2，OC=3，
B(2，3)，
将点B，C的坐标分别代入二次函数解析式，
，
，
抛物线解析式为：．（2分）
（2）如图，在对称轴上取一点E，连接EC、EB、EA，当点C、E、A三点共线时，EA+EC最小，即EAB的周长最小，
设直线解析式为：y=kx+b，
将点A、C的坐标代入可得：
，解得：，
一次函数解析式为：．（4分）
=，
D(1，4)，
令x=1，y==．
E(1，)．（6分）

（3）设直线CD解析式为：y=kx+b，
C(0，3)，D(1，4)，
,解得，直线CD解析式为：y=x+3，
同理求出射线BD的解析式为：y=－x+5(x≤2)，
设平移后的顶点坐标为(m，m+3)，
则抛物线解析式为：y=－(x－m)2+m+3，
①如图，当抛物线经过点B时，
－(2－m)2+m+3=3，解得m=1或4，（8分）
当1
②如图，当抛物线与射线恰好只有一个公共点H时，
将抛物线解析式与射线解析式联立可得：－(x－m)2+m+3=－x+5，即x2－(2m+1)x+m2－m+2=0，
要使平移后的抛物线与射线BD只有一个公共点，
即要使一元二次方程有两个相等的实数根，
，解得．（10分）
综上所述，或时，平移后的抛物线与射线BD只有一个公共点．

26．（12分）【详解】（1）证明：∵四边形为矩形，
∴，．
∵E为的中点，
∴．
∵，
∴，
∴，
∴；（2分）
（2）∵，
∴，
∴．
∵E为的中点，，
∴，
∴，
∴；（4分）
（3）①证明：∵，
∴，，
∴，
∴，
∴．（5分）
∵E为的中点，M为的中点，
∴，，
∴，即，
∴，
∴．
∵，
∴，
∴，即；（6分）
②设，，则，
∵，
∴，
解得：．（7分）
∵，
∴，
∴．
∵，，
∴，（8分）
∴．
在中，，
∴，
∴，
∴，（10分）
∴．
∵，
∴，
∴．（12分）
1
2
3
4
5
6
7
8
D
A
B
B
D
C
A
C