







数学北师大版(2021)1.3.1 交集课文配套课件ppt
展开目录 / CONTENTS
2001年-北京申奥成功
&vid=14586011872316940991
探讨下面两个情景实例:
实例1:到2022年年底举办过夏季奥运会的城市组成集合A ,举办过冬季奥运会的城市组成集合B,同时举办过两种奥运会的城市也组成一个集合C。
实例2:集合 M= {1, 2},集合 P={1, 2, 3},集合 Q ={ 1, 2, 5, 6}
三个集合中一个集合的元素是另外两个集合的公共元素。
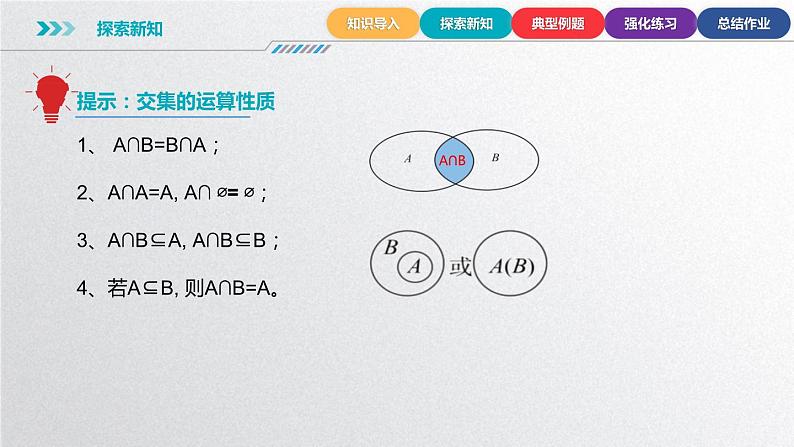
一般地, 设A, B是两个集合, 由属于A且属于B 的所有元素组成的集合C叫作集合A与集合B的交集, 记作A∩B, 读作“A 交B”,即 C=A∩B={x|x∈A, 且x∈B}。
设集合A={2, 3, 5, 7}, B={-2, 0, 3, 5, 8}, 求A∩B。
解:A∩B={3, 5}
分析:求交集就是求两集合的所有公共元素组成的集合,两集合中都有3, 5。
解:在数轴上将集合A与B表示出来, 观察可知 A∩B={x|-1
设集合A={x|x≤2}, B={x|x<-1}, 求A∩B。
解:在数轴上将集合A与B表示出来, 观察可知 A∩B={x|x<-1}。
分析:可先将已知集合在数轴上表示出来,然后观察得出交集。注意端点如图所示。
设集合A={(x, y)|x+2y-6=0}, B={(x, y)|x-4y=0}, 求A∩B。
分析:转化与划归的数学思想。 集合A就是方程x+2y-6=0的解集,集合B就是方程x-4y=0的解集,A,B的交集就是满足A和B方程的x,y的值,即联立两个方程所得二元一次方程组的解集。
两个或两个以上集合的交集运算1、如果集合是有限集,则需先把集合中的元素一一列举出来,然后选取共同的元素放在大括号里即可;2、如果集合是无限集,则常借助于数轴,把集合分别表示在数轴上,然后找到公共的范围就是所求。这样处理比较形象直观,但在解答过程中需注意端点问题;3、如果集合是方程的解集,则联立方程组求解即可。
{x|x 是等腰直角三角形}
(3)A∩B={(1, 2)}
(1)A∩B={x|x<−2}
1、学习指导与能力训练P17 水平一
1、学习指导与能力训练P18 水平二
数学高教版(2021)1.3 集合的运算课文ppt课件: 这是一份数学高教版(2021)<a href="/sx/tb_c4030579_t3/?tag_id=26" target="_blank">1.3 集合的运算课文ppt课件</a>,共18页。PPT课件主要包含了答案A∩B2,A∩B,B∩A,A∩A,A∩∅∅∩A∅,A∩B⊆A,A∩B⊆B,答案A∩B∅等内容,欢迎下载使用。
中职数学北师大版(2021)基础模块 上册1.3.1 交集优秀ppt课件: 这是一份中职数学北师大版(2021)基础模块 上册<a href="/sx/tb_c4036717_t3/?tag_id=26" target="_blank">1.3.1 交集优秀ppt课件</a>,文件包含中职数学北师大版基础模块上册第1单元《集合》第6课时交集课件pptx、中职数学北师大版基础模块上册第1单元《集合》第6课时交集教学设计doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
中职数学高教版(中职)基础模块上册(2021)1.3.1 交集评课ppt课件: 这是一份中职数学高教版(中职)基础模块上册(2021)1.3.1 交集评课ppt课件,文件包含13集合的运算课件pptx、13集合的运算教案pdf、13集合的运算docx等3份课件配套教学资源,其中PPT共43页, 欢迎下载使用。












