2025届高考数学一轮总复习第三章函数与基本初等函数课时规范练14函数模型及其应用

这是一份2025届高考数学一轮总复习第三章函数与基本初等函数课时规范练14函数模型及其应用，共7页。试卷主要包含了2时,y=4x等内容，欢迎下载使用。
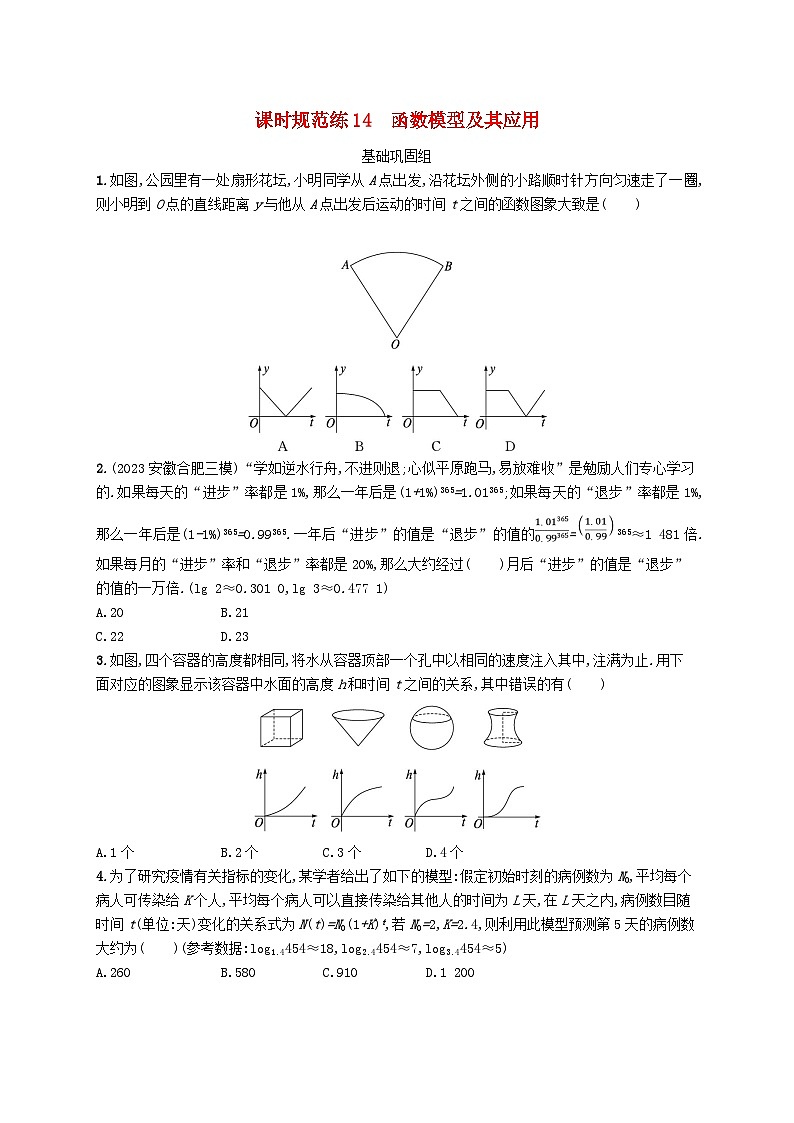
1.如图,公园里有一处扇形花坛,小明同学从A点出发,沿花坛外侧的小路顺时针方向匀速走了一圈,则小明到O点的直线距离y与他从A点出发后运动的时间t之间的函数图象大致是( )

2.(2023安徽合肥三模)“学如逆水行舟,不进则退;心似平原跑马,易放难收”是勉励人们专心学习的.如果每天的“进步”率都是1%,那么一年后是(1+1%)365=1.01365;如果每天的“退步”率都是1%,那么一年后是(1-1%)365=0.99365.一年后“进步”的值是“退步”的值的=365≈1 481倍.如果每月的“进步”率和“退步”率都是20%,那么大约经过( )月后“进步”的值是“退步”的值的一万倍.(lg 2≈0.301 0,lg 3≈0.477 1)
A.20B.21
C.22D.23
3.如图,四个容器的高度都相同,将水从容器顶部一个孔中以相同的速度注入其中,注满为止.用下面对应的图象显示该容器中水面的高度h和时间t之间的关系,其中错误的有( )
A.1个B.2个C.3个D.4个
4.为了研究疫情有关指标的变化,某学者给出了如下的模型:假定初始时刻的病例数为N0,平均每个病人可传染给K个人,平均每个病人可以直接传染给其他人的时间为L天,在L天之内,病例数目随时间t(单位:天)变化的关系式为N(t)=N0(1+K)t,若N0=2,K=2.4,则利用此模型预测第5天的病例数大约为( )(参考数据:lg1.4454≈18,lg2.4454≈7,lg3.4454≈5)
A.260B.580C.910D.1 200
5.(多选)某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,y关于x的函数图象如图①所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图②、图③中的实线分别为调整后y关于x的函数图象.给出下列四种说法,其中正确的是( )
A.图②对应的方案是:提高票价,并提高固定成本
B.图②对应的方案是:保持票价不变,并降低固定成本
C.图③对应的方案是:提高票价,并保持固定成本不变
D.图③对应的方案是:提高票价,并降低固定成本
6.某品牌行车记录仪支架销售公司从2021年1月起开展网络销售与实体店体验安装结合的销售模式.根据几个月运营发现,产品的月销量x(单位:万件)与投入实体店体验安装的费用t(单位:万元)之间满足函数关系式x=3-.已知该公司每月固定的各种费用支出为3万元,产品每1万件进货价格为32万元.若每件产品的售价定为“进货价的150%”与“平均每件产品的实体店体验安装费用的一半”之和,则该公司最大月利润为 万元.
7.某公司为加大核心技术的研发投入,建立了一套关键部件的评价标准:耐久度f(x)与时间x(单位:小时)的函数关系为f(x)=-k+3k+1,x∈[0,24),k∈[0,1].
(1)令g(x)=,x∈[0,24),求g(x)的最大值;
(2)若f(x)的最大值记为h(k),求函数h(k)的表达式;
(3)若当h(k)≤4时,表示耐久度达到标准.则当实数k在什么范围内时,该部件耐久度达到标准?
综合提升组
8.为预防病毒感染,学校每天定时对教室进行喷洒消毒.已知教室内每立方米空气中的含药量y(单位:mg)随时间x(单位:h)的变化如图所示,在药物释放过程中,y与x成正比;药物释放完毕后,y与x的函数关系式为y=x-a(a为常数),则( )
A.当0≤x≤0.2时,y=4x
B.当x>0.2时,y=x-0.1
C.小时后,教室内每立方米空气中的含药量降低到0.25 mg以下
D.小时后,教室内每立方米空气中的含药量降低到0.25 mg以下
9.公安部交通管理局下发《关于2019年治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局发布的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阈值见下表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的散点图如图所示,且该图表示的函数模型f(x)=假设该人喝一瓶啤酒后至少经过n(n∈N*)小时才可以驾车,则n的值为( )(参考数据:ln 15≈2.71,ln 30≈3.40)
车辆驾驶人员血液酒精含量阈值
A.7B.6C.5D.4
10.(2023北京海淀一模)如图,假定P,Q两点以相同的初速度运动.点Q沿直线CD做匀速运动,CQ=x;点P沿线段AB(长度为107单位)运动,它在任何一点的速度值等于它尚未经过的距离(PB=y).令点P与Q同时分别从点A,C出发,定义x为y的纳皮尔对数,用现代数学符号表示x与y的对应关系就是y=107(e=2.718 28…),当点P从线段AB上靠近点A的三等分点移动到中点时,经过的时间为( )
A.ln 2B.ln 3
C.lnD.ln
创新应用组
11.经过市场调研发现,某公司生产的某种时令商品在未来一个月(30天)内的日销售量m(t)(单位:百件)与时间第t天的关系如下表所示.
未来30天内,受市场因素影响,前15天此商品每天每件的利润f1(t)(单位:元)与时间第t天的函数关系式为f1(t)=-3t+88(1≤t≤15,且t为整数),而后15天此商品每天每件的利润f2(t)(单位:元)与时间第t天的函数关系式为f2(t)=+2(16≤t≤30,且t为整数).
(1)现给出以下两种函数模型:①m(t)=kt+b(k,b为常数);②m(t)=b·at(a,b为常数,a>0且a≠1).分析表格中的数据,请说明哪种函数模型更合适,并求出该函数解析式;
(2)若这30天内该公司此商品的日销售利润始终不能超过4万元,则考虑转型.请判断该公司是否需要转型?并说明理由.
课时规范练14 函数模型及其应用
1.D
解析小明沿走时,与点O的直线距离保持不变,沿BO走时,随时间增加与点O的距离越来越小,沿OA走时,随时间增加与点O的距离越来越大,故选D.
2.D
解析设大约经过x月“进步“的值是“退步”的值的10000倍,则10000×(1-0.2)x=1.2x,即x=10000,∴x=≈23,故选D.
3.A
解析选项A中因为正方体的底面积是定值,所以水面高度的增加是均匀的,即图象是直线型的,故A错误;选项B中因为几何体下面窄上面宽,且相同的时间内注入的水量相同,所以下面的高度增加得快,上面增加得慢,即图象应越来越平缓,故B正确;选项C中因为球体是对称的几何体,下半球因下面窄上面宽,所以水的高度增加得越来越慢,上半球恰恰相反,所以水的高度增加得越来越快,则图象先陡峭再变缓再变陡,故C正确;选项D中几何体两头宽、中间窄,所以水的高度增加得越来越快后再越来越慢,则图象先平缓再变陡再变缓,故D正确.故选A.
4.C
解析N(5)=2(1+2.4)5=2×3.45,因为lg3.4454≈5,所以3.45≈454,所以N(5)=2×3.45≈2×454=908≈910,故选C.
5.BC
解析由图①可设y关于x的函数为y=kx+b,k>0,b