2025届高考数学一轮总复习第八章立体几何与空间向量课时规范练41直线平面垂直的判定与性质

这是一份2025届高考数学一轮总复习第八章立体几何与空间向量课时规范练41直线平面垂直的判定与性质，共13页。
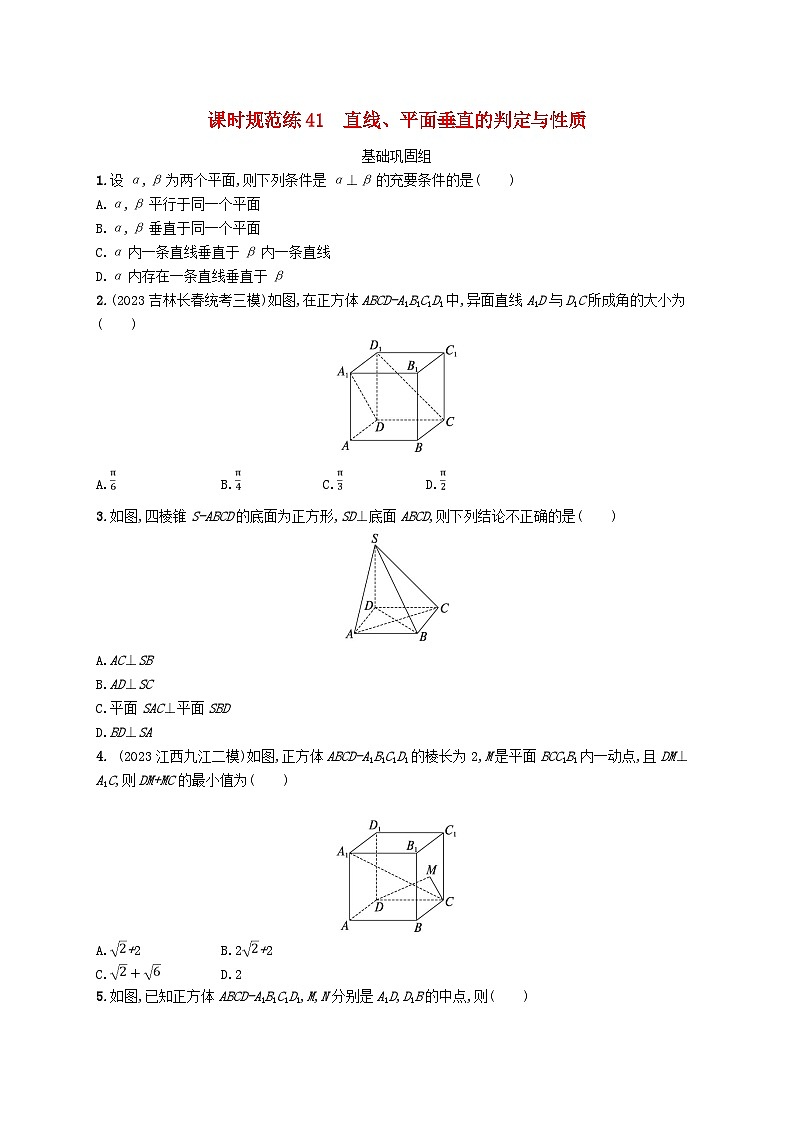
1.设α,β为两个平面,则下列条件是α⊥β的充要条件的是( )
A.α,β平行于同一个平面
B.α,β垂直于同一个平面
C.α内一条直线垂直于β内一条直线
D.α内存在一条直线垂直于β
2.(2023吉林长春统考三模)如图,在正方体ABCD-A1B1C1D1中,异面直线A1D与D1C所成角的大小为( )
A.B.C.D.
3.如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论不正确的是( )
A.AC⊥SB
B.AD⊥SC
C.平面SAC⊥平面SBD
D.BD⊥SA
4. (2023江西九江二模)如图,正方体ABCD-A1B1C1D1的棱长为2,M是平面BCC1B1内一动点,且DM⊥A1C,则DM+MC的最小值为( )
A.+2B.2+2
C.D.2
5.如图,已知正方体ABCD-A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
6.在正方体ABCD-A1B1C1D1中,E,F分别为AB,BC的中点,则( )
A.平面B1EF⊥平面BDD1
B.平面B1EF⊥平面A1BD
C.平面B1EF∥平面A1AC
D.平面B1EF∥平面A1C1D
7.已知α,β是两个不同的平面,l,m是两条不同的直线,l⊥α,m⊂β,下列四个推论:①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l⊥m⇒α∥β;④l∥m⇒α⊥β.其中正确的推论是 .(填序号)
8.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,AC∩BD=O,M是PC上的一动点,当点M满足 时,平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可)
9. 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=a.求证:
(1)PD⊥平面ABCD;
(2)平面PAC⊥平面PBD.
综合提升组
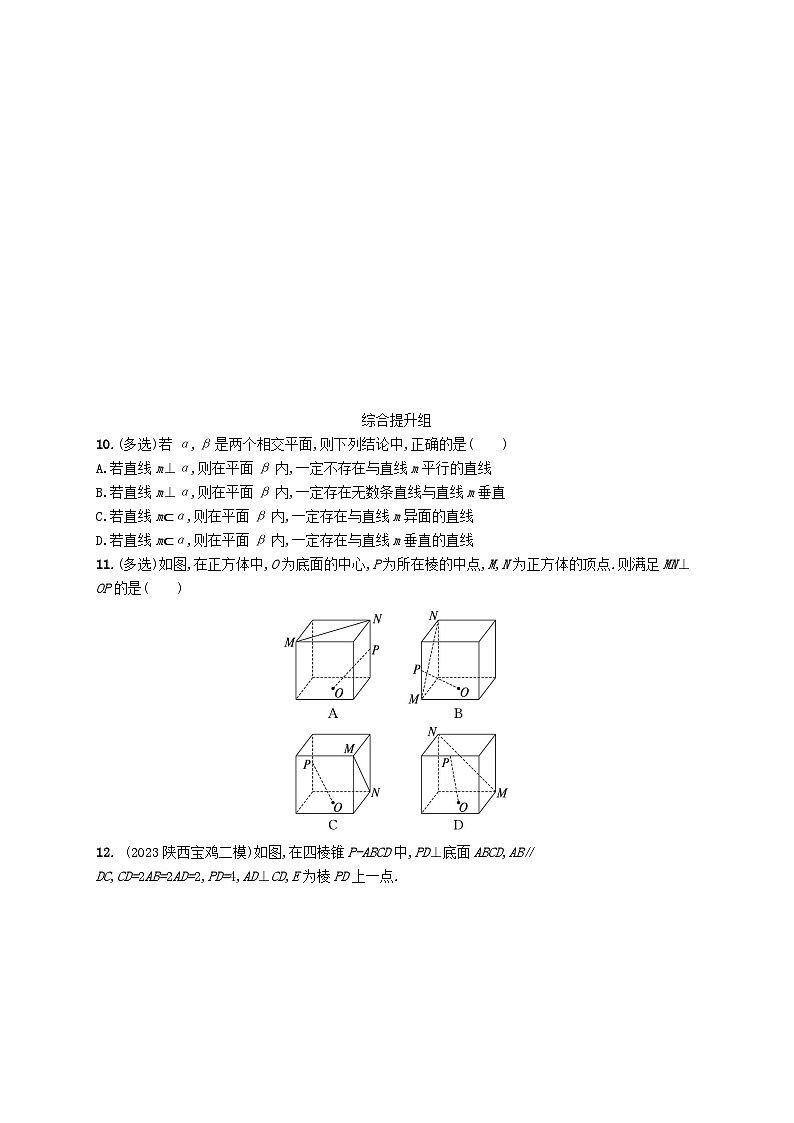
10.(多选)若α,β是两个相交平面,则下列结论中,正确的是( )
A.若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线
B.若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直
C.若直线m⊂α,则在平面β内,一定存在与直线m异面的直线
D.若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线
11.(多选)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足MN⊥OP的是( )
12. (2023陕西宝鸡二模)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,CD=2AB=2AD=2,PD=4,AD⊥CD,E为棱PD上一点.
(1)求证:无论点E在棱PD的任何位置,都有CD⊥AE成立;
(2)若在PB上存在一点H,且PH=2HB,求三棱锥C-ABH的体积.
13.(2023四川成都二模)如图,三棱柱ABC-A1B1C1中,△A1B1C1与△AB1C1均是边长为2的正三角形,且AA1=.
(1)求证:平面AB1C1⊥平面A1B1C1;
(2)求四棱锥A-BB1C1C的体积.
14. 在五面体EF-ABCD中,正方形CDEF所在平面与平面ABCD垂直,四边形ABCD为等腰梯形,AB∥CD,AD=DC=BC=AB.
(1)求证:平面BCF⊥平面ACE;
(2)若三棱锥A-BCE的体积为,求线段AB的长.
创新应用组
15. (2023陕西渭南一模)如图,在直三棱柱ABC-A1B1C1中,E为A1C1的中点,AB=BC=2,C1F⊥AB.
(1)求证:AB⊥BC;
(2)若C1F∥平面ABE,且C1F=2,求点A到平面BCE的距离.
16. (2023江西九江十校联考二)如图,四边形ABCD是正方形,ABEF是矩形,平面ABCD⊥平面ABEF,AF=AB=2,G是EF上一点,且EG=m(0