陕西省西安八校2024届高三下学期联考理科数学试题(无答案)

这是一份陕西省西安八校2024届高三下学期联考理科数学试题(无答案)，共6页。试卷主要包含了保持纸面清洁，不折叠，不破损，的展开式的常数项为等内容，欢迎下载使用。

注意事项：
1．答题前，考生务必先将自己的姓名、准考证号填写在答题纸上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题纸上的指定位置上．
2．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整，笔迹清楚．
3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．
4．保持纸面清洁，不折叠，不破损．
5．若做选考题时，考生应按照题目要求作答，并在答题纸上对应的题号后填写．
第Ⅰ卷（选择题 共60分）
一、选择题（共12小题，每小题5分，共60分．每小题给出的四个选项中，只有一个选项符合题目要求）
1．已知全集，集合，，则（ ）．
A．B．C．D．
2．是虚数单位，复数，，（是的共轭复数），则（ ）．
A．B．C．D．
3．已知函数的周期是3，则的周期为（ ）．
A．B．3C．6D．9
4．已知函数的部分图像如图所示，则
（ ）．
（第4题图）
A．B．C．0D．
5．已知等差数列的公差为，前项和为，则“”是“”的（ ）．
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
6．之前7年，我国生活垃圾无害处理量如下表：
通过计算，，，，线性相系数则（ ）．
A．与的线性相关性很强，用线性回归模型拟合与的关系比较好
B．与的线性相关性比较弱，可以用线性回归模型拟合与的关系
C．与不线性相关，用线性回归模型拟合与的关系，会有很大误差
D．与不线性相关，不可以用线性回归模型拟合与的关系
7．已知函数有极值点在闭区间上，则的取值范围为（ ），
A．B．C．D．
8．一个正四棱锥的主视图如图所示，，则该四棱锥的表面积为（ ）．
（第8题图）
A．B．C．46D．48
9．的展开式的常数项为（ ）．
A．B．C．480D．736
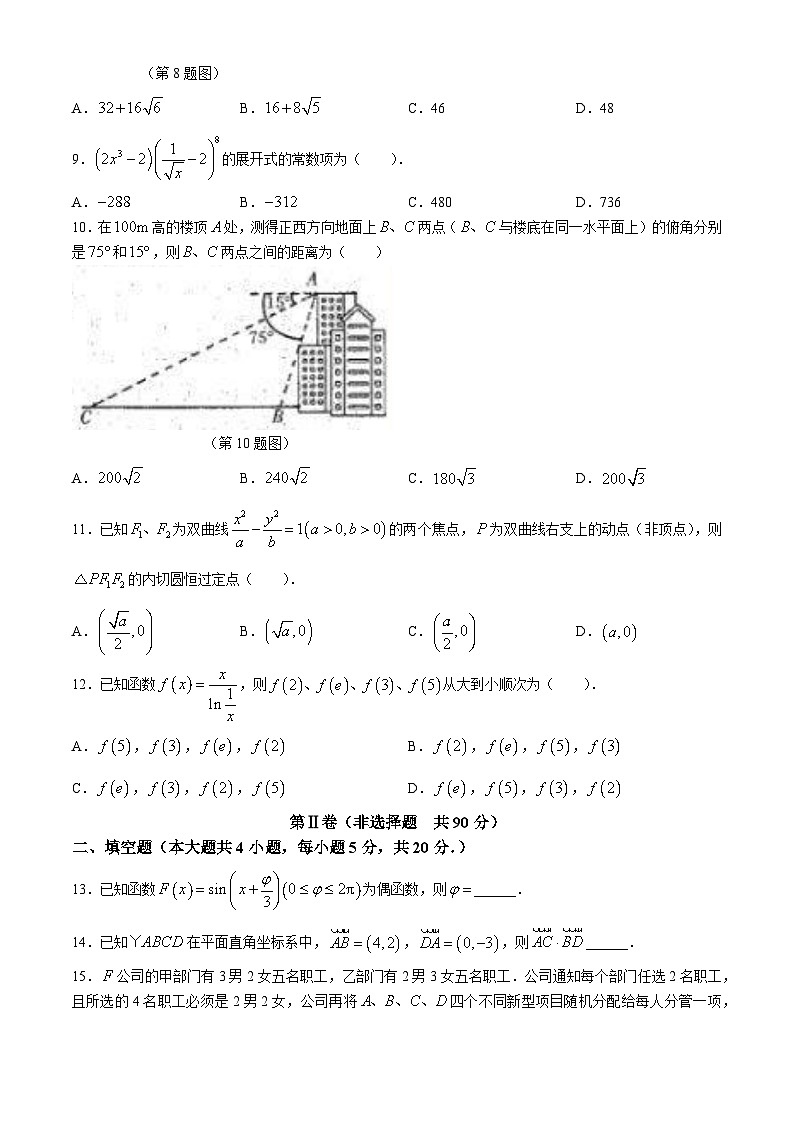
10．在高的楼顶处，测得正西方向地面上两点（与楼底在同一水平面上）的俯角分别是和，则两点之间的距离为（ ）
（第10题图）
A．B．C．D．
11．已知为双曲线的两个焦点，为双曲线右支上的动点（非顶点），则的内切圆恒过定点（ ）．
A．B．C．D．
12．已知函数，则从大到小顺次为（ ）．
A．，，，B．，，，
C．，，，D．，，，
第Ⅱ卷（非选择题 共90分）
二、填空题（本大题共4小题，每小题5分，共20分．）
13．已知函数为偶函数，则______．
14．已知在平面直角坐标系中，，，则______．
15．公司的甲部门有3男2女五名职工，乙部门有2男3女五名职工．公司通知每个部门任选2名职工，且所选的4名职工必须是2男2女，公司再将四个不同新型项目随机分配给每人分管一项，则不同的分配方案种数为（用数字作答）______．
16．已知函数，，，则的概率为______．
三、解答题（共7小题，共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题．第22、23题为选考题，考生根据要求作答）
（一）必考题：共60分．
17．（本小题满分12分）已知数列满足，，．
（Ⅰ）写出数列的前五项，由此五项，写出数列的一个通项公式（不需要证明）；
（Ⅱ）求数列的前项和．
18．（本小题满分12分）
“民政送温暖，老人有饭吃”．近年来，各级政府，重视提高老年人的生活质量．在医疗、餐饮等多方面，为老人提供了方便．单从用餐方面，各社区，创建了“爱心食堂”、“爱心午餐”、“老人食堂”等等不同名称的食堂，解决了老人的吃饭问题．“爱心食堂A”为了更好地服务老人，于3月28日12时，食堂管理层人员对这一时刻用餐的118人，对本食堂推出的15种菜品按性价比“满意”和“不满意”作问卷调查，其中，有13人来食堂用餐不足5次，另有儿童5人，他们对菜品不全了解，不予问卷统计，在被问卷的人员中男性比女性多20人．用餐者对15种菜品的性价比认为“满意”的菜品数记为，当时，认为该用餐者对本食堂的菜品“满意”，否则，认为“不满意”。统计结果部分信息如下表：
（Ⅰ）①完成上面列联表；
②能有多大（百分比）的把握认为用餐者对本食堂菜品的性价比是否满意与性别有关？
（Ⅱ）用分层抽样在对菜品的性价比“满意”的人群中抽取6人，再从这6人中随机抽取3人，用表示抽取的3人中的男性人数，求的分布列和期望．
附：参考公式和临界值表，其中，．
19．（本小题满分12分）
如图，在直三棱柱中，是上的点，且平面．
（第19题图）
（Ⅰ）求证：平面；
（Ⅱ）若，，，是棱上的点，且直线与平面所成角的正弦值为，试确定点的位置．
20．（本小题满分12分）
在直角坐标系中，动点到定点的距离比点到轴的距离大2．
（Ⅰ）求动点的轨迹的方程；
（Ⅱ）过轴上的点的任意直线，交轨迹于不同两点和，交轴于，且，，求的值．
21．（本小题满分12分）
已知函数，的图像在处的切线过原点．
（Ⅰ）求的值；
（Ⅱ）设，，若对总，使成立，求的取值范围．
（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．并请考生务必将答题卡中对所选试题的题号进行涂写．
22．[选修4-4 极坐标与参数方程]（本小题满分10分）
在平面直角坐标系中，圆的参数方程为（为参数），直线过点．以原点为极点，轴正半轴为极轴建立极坐标系．
（Ⅰ）若直线还经过点，的极坐标为，求直线的极坐标方程；
（Ⅱ）若直线与圆有公共点，直线的倾斜角为，求的取值范围．
23．[选修不等式选讲]（本小题满分10分）．
已知函数．
（Ⅰ）若，设，求的最小值及取最小值时的值；
（Ⅱ）若关于的方程有三个解，求实数取值范围．
序号
1
2
3
4
5
6
7
（年）
1
2
3
4
5
6
7
（处理量）
满意
不满意
合计
男
40
女
20
合计
0.100
0.050
0.010
0.001
2.706
3.841
6.635
10.828