北京市房山区2024年中考一模数学试卷(含答案)

这是一份北京市房山区2024年中考一模数学试卷(含答案)，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．如图是某几何体的三视图，则该几何体是( )
A.圆柱B.圆锥C.三棱柱D.球
2．据中国国家铁路集团有限公司消息：在2024年为期40天的春运期间，全国铁路累计发送旅客亿人次，日均发送12089000人次.将12089000用科学记数法表示应为( )
A.B.C.D.
3．如图四个博物馆标志，其文字上方的图案既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
4．如图，，点A，C在直线a上，点B在直线b上，，若，则的度数是( )
A.B.C.D.
5．若关于x的一元二次方程有两个相等的实数根，则实数m的值为( )
A.B.C.D.
6．不透明的袋子中装有1个红球，1个白球，除颜色外两个小球无其他差别，从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么两次都摸到红球的概率是( )
A.B.C.D.
7．若，则下列结论正确的是( )
A.B.C.D.
8．如图，在四边形中，，点E在上，，连接并延长交的延长线于点F，连接，.给出下面三个结论：
①；
②；
③.上述结论中，所有正确结论的序号是( )
A.①②B.②③C.①③D.①②③
二、填空题
9．若代数式有意义，则实数x的取值范围是________.
10．分解因式：________.
11．方程的解为________.
12．在平面直角坐标系中，若点，在反比例函数的图象上，则________（填“>”，“=”或“<”）.
13．某校为了调查学生家长对课后服务的满意度，从600名学生家长中随机抽取150名进行问卷调查，获得了他们对课后服务的评分数据（评分记为x），数据整理如下：
根据以上数据，估计这600名学生家长评分不低于80分的有________名.
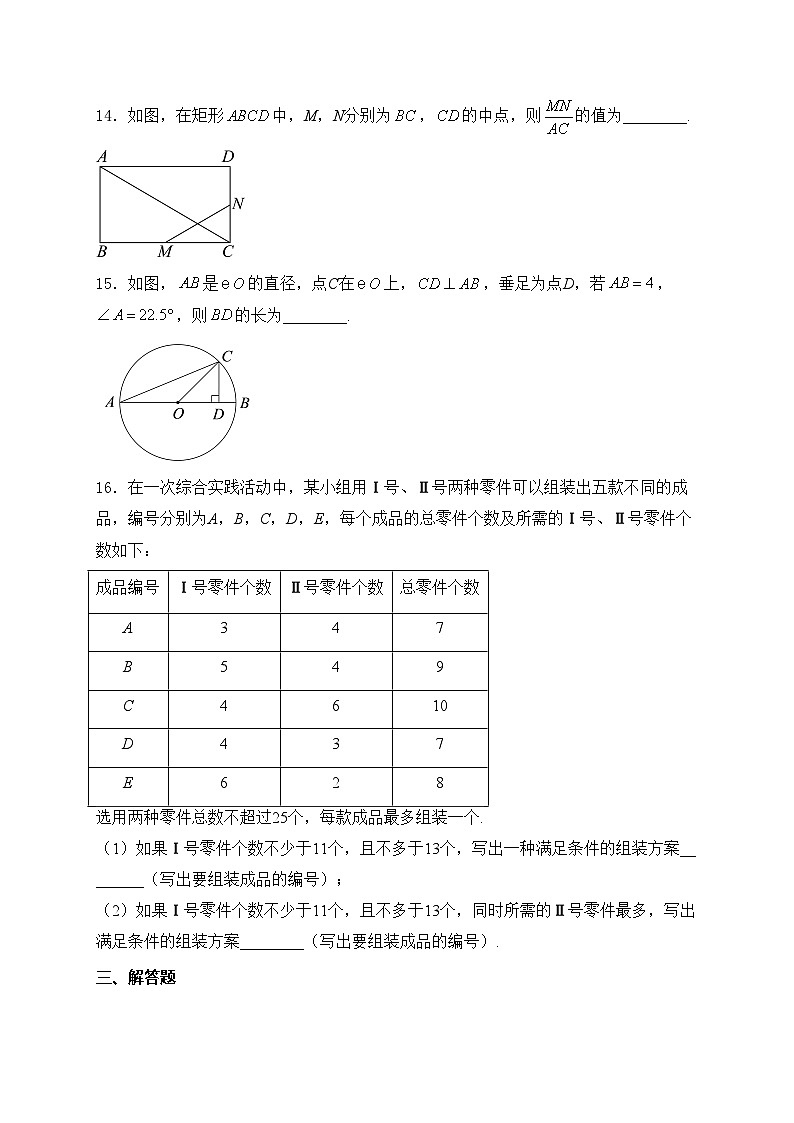
14．如图，在矩形中，M，N分别为，的中点，则的值为________.
15．如图，是的直径，点C在上，，垂足为点D，若，，则的长为________.
16．在一次综合实践活动中，某小组用Ⅰ号、Ⅱ号两种零件可以组装出五款不同的成品，编号分别为A，B，C，D，E，每个成品的总零件个数及所需的Ⅰ号、Ⅱ号零件个数如下：
选用两种零件总数不超过25个，每款成品最多组装一个.
（1）如果Ⅰ号零件个数不少于11个，且不多于13个，写出一种满足条件的组装方案________（写出要组装成品的编号）；
（2）如果Ⅰ号零件个数不少于11个，且不多于13个，同时所需的Ⅱ号零件最多，写出满足条件的组装方案________（写出要组装成品的编号）.
三、解答题
17．计算：.
18．解不等式组：
19．已知，求分式的值.
20．在房山区践行“原色育人，生态发展”教育发展理念的引领下，某校为提升实践育人实效，积极组织学生建设劳动基地，参与校园种植活动.计划在校园内一块矩形的空地上开垦两块完全相同的矩形菜园，如图所示，已知空地长10米，宽米，矩形菜园的长与宽的比为，并且预留的上、中、下、左、右通道的宽度相等，那么预留通道的宽度和矩形菜园的宽分别是多少米？
21．如图，在中，，交于点O，，过点D作交延长线于点E.
（1）求证：四边形是菱形；
（2）若，，求的长.
22．在平面直角坐标系中，函数的图象由函数的图象平移得到，且经过点.
（1）求该函数的解析式；
（2）当时，对于x的每一个值，函数的值大于函数的值，直接写出m的取值范围.
23．2024年1月3日北京市生态环境局召开了“2023年北京市空气质量”新闻发布会，通报了2023年北京市空气质量状况：北京2023年年均浓度为32微克/立方米，最长连续优良天数为192天，“北京蓝”已成为常态.下面对2023年北京市九个区月均浓度的数据进行整理，给出了部分信息：
a.2023年9月和10月北京市九个区月均浓度的折线图：
b.2023年9月和10月北京市九个区月均浓度的平均数、中位数、众数：
（1）写出表中m，n的值；
（2）2023年9月北京市九个区月均浓度的方差为，2023年10月北京市九个区月均浓度的方差为，则______（填“>”，“=”或“<”）；
（3）2013年至2023年，北京市空气优良级别达标天数显著增加，2013年空气优良达标天数为176天，2023年比2013年增幅达到约，2023年达标天数约为______天.
24．如图，是的直径，点C是上一点，过点C作的切线与的延长线交于点D，过点B作，与交于点E，连接，.
（1）求证：；
（2）若，，求的长.
25．如图，点P是半圆O的直径上一动点，点Q是半圆O内部的一定点，作射线交于点C，连接.已知，设的长度为，的长度为，的长度为.（当点P与点A重合时，x的值为0）.

小山根据学习函数的经验，对函数，随自变量x的变化而变化的规律进行探究.对于点P在上的不同位置，画图、测量，得到了x，，的几组值，如下表：
（1）在同一平面直角坐标系中，小山已画出函数的图象，请你画出函数的图象；
（2）结合函数图象，解决问题：
①当的长度为时，则的长度约为_____cm（结果保留小数点后一位）.
②当为等腰三角形时，则的长度约为_____cm（结果保留小数点后一位）.
26．在平面直角坐标系中，，是抛物线上任意两点.
（1）当时，求抛物线与轴的交点坐标及顶点坐标；
（2）若对于，，都有，求a的取值范围.
27．在中，，，D是上的动点(不与点C重合)，且，连接，将射线绕点A顺时针旋转得到射线，过点D作交射线于点E，连接，在上取一点H，使，连接.
（1）依题意补全图形；
（2）直接写出的大小，并证明.
28．在平面直角坐标系中，将中心为M的等边三角形记作等边三角形M，对于等边三角形M和点P（不与O重合）给出如下定义：若等边三角形M的边上存在点N，使得直线与以为半径的相切于点P，则称点P为等边三角形M的“相关切点”.
（1）如图，等边三角形M的顶点分别为点，，.
①在点，，中，等边三角形M的“相关切点”是_____；
②若直线上存在等边三角形M的“相关切点”，求b的取值范围；
（2）已知点，等边三角形M的边长为.若存在等边三角形M的两个“相关切点”E，F，使得为等边三角形，直接写出m的取值范围.
参考答案
1．答案：B
解析：长方体的三视图都是圆锥，
故选：B.
2．答案：C
解析：将12089000用科学记数法表示应为，
故选：C.
3．答案：B
解析：A、原图是轴对称图形，但不是中心对称图形，故本选项不符合题意；
B、原图既是中心对称图形，又是轴对称图形，故本选项符合题意；
C、原图既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；
D、原图是轴对称图形，但不是中心对称图形，故本选项不符合题意.
故选：B.
4．答案：D
解析：，
，
又
，
，
故选D.
5．答案：B
解析：根据题意得，
解得，
即m的值为，
故选：B.
6．答案：C
解析：画树状图如下：
共有4种等可能的结果，其中两次都摸到红球的结果有1种，
两次都摸到红球的概率是，
故选：C.
7．答案：C
解析：，
，
.
故选：C.
8．答案：D
解析：，
，，，
，
，
，
，故①正确，符合题意；
，且，
，故②正确，符合题意；
，，
，
，
，，
，
，
，
，故③正确，符合题意；
故选：D.
9．答案：
解析：有意义，
，
.
故答案为.
10．答案：
解析：，
故答案为：.
11．答案：
解析：原方程去分母得：，
解得：，
检验：当时，，
故原方程的解为，
故答案为：.
12．答案：<
解析：，，
反比例函数图象在第一、三象限，在每个象限内随的增大而减小，
，
，
故答案为：<.
13．答案：360
解析：由题意得：（名），
即估计这600名学生家长评分不低于80分的有360名，
故答案为：360.
14．答案：
解析：连接，
四边形是矩形，
，
M，N分别为，的中点，
是是中位线，
，
，
故答案为：.
15．答案：
解析：，
，
，
，
，
，
，
故答案为：.
16．答案：（答案不唯一）；
解析：（1）设Ⅰ号零件个数为x，Ⅱ号零件的个数为y，
Ⅰ号零件个数不少于11个，且不多于13个，
，
由表得满足Ⅰ号零件的组法为：
组用Ⅰ号零件12个，组用Ⅰ号零件12个，组用Ⅰ号零件11个，组用Ⅰ号零件13个，组用Ⅰ号零件13个，组用Ⅰ号零件13个，
以上六种方案中使用Ⅱ号零件个数为：
组用Ⅱ号零件14个，组用Ⅱ号零件11个，组用Ⅱ号零件13个，组用Ⅱ号零件13个，组用Ⅱ号零件12个，组用Ⅱ号零件9个，
两种零件总数不超过25个，
，
满足题意的方案为组，，，，
一种满足条件的组装方案可以是，
故答案为：；
（2）由（1）得，组用的零件最多，为25个，
故答案为：.
17．答案：5
解析：

.
18．答案：
解析：原不等式组为，
解不等式①，得.
解不等式②，得.
原不等式组的解集为.
19．答案：，
解析：

.
，
.
原式.
20．答案：预留通道的宽度是米，矩形菜园的宽是米
解析：设矩形菜园的宽为x米，则矩形菜园的长为米.
由题意可得，
.
解得.
.
答：预留通道的宽度是米，矩形菜园的宽是米.
21．答案：（1）见解析
（2）
解析：（1）证明：四边形是平行四边形，
.
.
，
.
.
四边形是菱形.
（2）四边形是菱形，
，，.
∵，
.
，
.
，
.
在中，，.
.
.
22．答案：（1）
（2）
解析：（1）函数的图象平行于函数的图象，
，
把代入，得：，
解得，，
该函数的表达式为；
（2）当函数的值大于函数的值时，，
，
当时，对于x的每一个值，函数的值大于函数的值，
，
.
23．答案：（1），
（2）<
（3）271
解析：（1）将九月份的数据从小到大排列为：26、26、26、29、30、31、31、33、34
根据中位数和众数的概念，
可以知道这组数据的第五个数为30，即中位数为，
这组数据26出现的次数最多，即众数为；
（2）根据折线图可以看出，九月份的数据大约分布于26至34，十月份的数据大约分布于32至42，
可以发现九月份的数据比十月份的数据波动较小，更加稳定，
所以九月份数据的方差小于十月份数据的方差，
故答案为：<.
（3）根据已知条件可以列式为：（天
故答案为：271.
24．答案：（1）见解析
（2）
解析：（1）证明：，
，
又，
.
.
（2）连接，交于点F，如图所示：
是的切线，切点为C，
，
，
，
，
F为中点.
O为直径中点，
为的中位线，
，
，
.
，
，
，
，
是的直径，
，
在中
，
，
由勾股定理得.
.
.
F为中点，，
.
在中，由勾股定理得
.
25．答案：（1）见详解
（2）①
②，，
解析：（1）函数图象如图示：
（2）①当时，由图像可知，
故答案为9.2.
②当时，即，观察两个函数图像交点的横坐标即为长，由图象得
；
当时，即，画出函数图象，如图示：
观察图像即为直线与函数图像交点，故；
当时，即，观察图像即为直线与函数图像交点，故.
故答案为：，，.
26．答案：（1）抛物线与轴的交点坐标为，抛物线的顶点坐标为
（2）
解析：（1）令，则.
当时，.
抛物线与轴的交点坐标为；
，
当时，抛物线的顶点坐标为.
（2），是抛物线上任意两点，
，.
.
，，
，.
，，
.即.
.
.
27．答案：（1）见解析
（2），见解析
解析：（1）依题意补全图形，如图.
（2）结论：.
理由：过点A作于点T，设，交于点O.
，，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
.
28．答案：（1）①，
②
（2）或
解析：（1）①如图，
根据题意，直线与以为半径的相切，
由图可知，等边三角形M的“相关切点”是，，
故答案为：，；
②根据题意，满足题意的P点是以，半径为1的弧上，如图，
若直线上存在等边三角形M的“相关切点”，如图，
由，是等腰直角三角形，，
，
，即，
，
，，
，
此时，
b的取值范围为；
（2）如图，此时中，，，
此时，，
解得：（负值舍去），
如图，此时中，，，
此时，，
解得：（正值舍去），
如图，
此时，，
解得：或（舍去），
如图，
此时，，
解得：（舍去）或，
综上可知：或.
家长评分
人数
15
45
60
30
成品编号
Ⅰ号零件个数
Ⅱ号零件个数
总零件个数
A
3
4
7
B
5
4
9
C
4
6
10
D
4
3
7
E
6
2
8
月均浓度
平均数
中位数
众数
9月
m
n
10月
36
36
0
1
2
3
4
5
6
7
8
9
10
4.32
4.91
5.78
6.93
8.08
8.81
9.18
9.37
9.48
9.55
9.60
9.02
7.86
6.63
5.46
4.79
5.00
5.73
6.64
7.61
8.60
9.60