备考2024年中考数学核心素养专题二十三 函数的综合问题练习附解析

这是一份备考2024年中考数学核心素养专题二十三 函数的综合问题练习附解析，共44页。试卷主要包含了选择题，填空题，解答题，综合题，实践探究题等内容，欢迎下载使用。
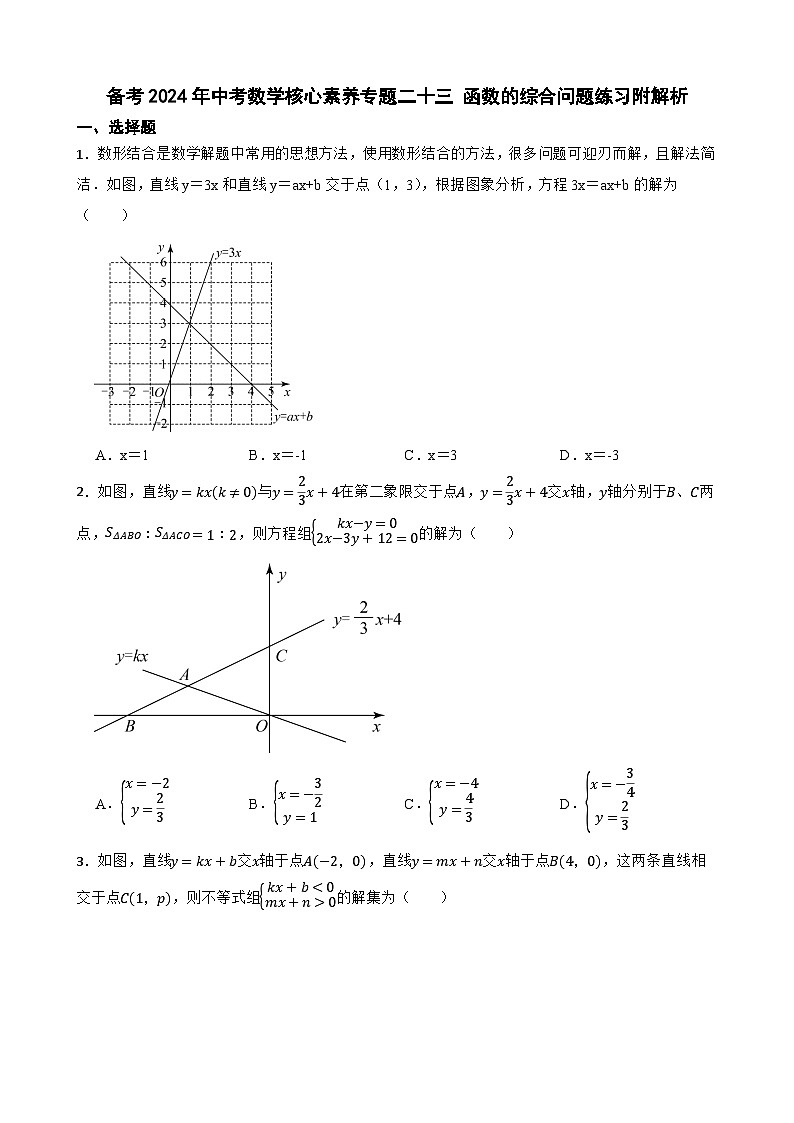
1．数形结合是数学解题中常用的思想方法，使用数形结合的方法，很多问题可迎刃而解，且解法简洁．如图，直线y＝3x和直线y＝ax+b交于点（1，3），根据图象分析，方程3x＝ax+b的解为（ ）
A．x＝1B．x＝-1C．x＝3D．x＝-3
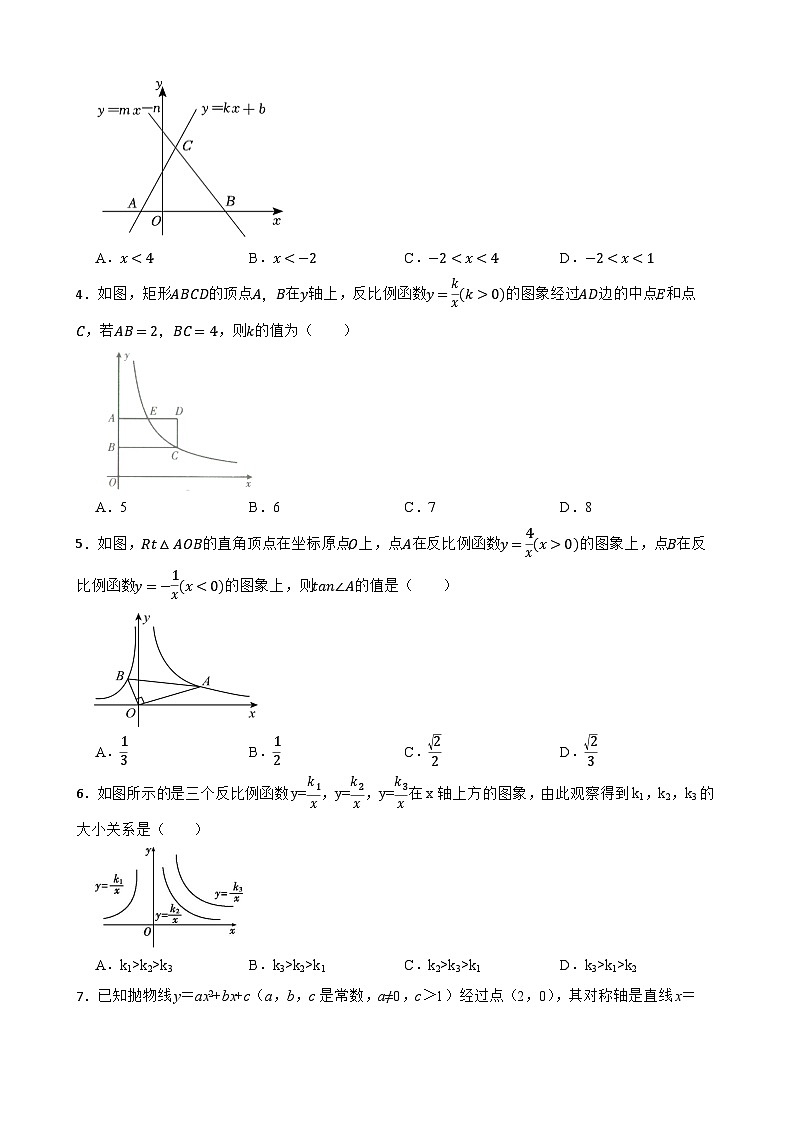
2．如图，直线y=kx(k≠0)与y=23x+4在第二象限交于点A，y=23x+4交x轴，y轴分别于B、C两点，SΔABO：SΔACO=1：2，则方程组kx−y=02x−3y+12=0的解为（ ）
A．x=−2y=23B．x=−32y=1C．x=−4y=43D．x=−34y=23
3．如图，直线y=kx+b交x轴于点A(−2，0)，直线y=mx+n交x轴于点B(4，0)，这两条直线相交于点C(1，p)，则不等式组kx+b0的解集为（ ）
A．xk3>k1D．k3>k1>k2
7．已知抛物线y＝ax2+bx+c（a，b，c是常数，a≠0，c＞1）经过点（2，0），其对称轴是直线x＝12，有下列结论：①abc＞0；
②关于x的方程ax2+bx+c＝a有两个不等的实数根；
③a＜﹣12．
其中，正确结论的个数是（ ）
A．0B．1C．2D．3
8．已知二次函数y=a(x+1)(x−m)(a为非零常数，10)图象上，
∴2×（m+2）=4m，
解得：m=2，
∴点C的坐标为（4，2），
再将点C（4，2）代入y=kx(k>0)可得：k=4×2=8，
故答案为：D.
【分析】设点C的坐标为（4，m），再求出点D的坐标为（4，m+2），点A的坐标为（0，m+2），点B的坐标为（0，m），利用中点坐标公式可得点E的坐标为（2，m+2），再将点E、C的坐标代入y=kx(k>0)可得2×（m+2）=4m，求出m的值，再求出点C的坐标，最后将点C的坐标代入y=kx(k>0)求出k的值即可.
5．【答案】B
【解析】【解答】解：如图，过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，
∴∠BCO=∠ADO=90°，
∵点A、B分别在反比例函数y=4x(x>0)与y=−1x(x