2025届高考数学一轮总复习第八章立体几何与空间向量第四节空间直线平面的垂直课件

这是一份2025届高考数学一轮总复习第八章立体几何与空间向量第四节空间直线平面的垂直课件，共60页。PPT课件主要包含了强基础增分策略，知识梳理，不大于，0°90°，a⊥α，半平面，直二面角，b⊥α，答案A，增素能精准突破等内容，欢迎下载使用。
1.直线与直线垂直(1)两条直线所成的角:平面内两条直线相交形成4个角,其中　　 　90°的角称为两条直线所成的角(或夹角). (2)异面直线所成的角:已知两条异面直线a,b,经过空间任一点O分别作直线a'∥a,b'∥b,把直线a'与b'所成的角叫做异面直线a与b所成的角(或夹角).
角的大小与点O的位置无关
(3)空间两条直线所成角的取值范围是　　　　　　. (4)两条异面直线互相垂直:如果两条异面直线所成的角是　　　　　,称这两条异面直线互相垂直. 
微思考能给空间两条直线的互相垂直下个定义吗?
提示 如果空间两条直线所成的角是直角,称这两条空间直线互相垂直.
2.直线与平面垂直(1)定义:一般地,如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的　　　　,平面α叫做直线l的　　　　.直线与平面垂直时,它们唯一的公共点P叫做垂足. 
与“所有直线”是同义的,但与“无数条”不同
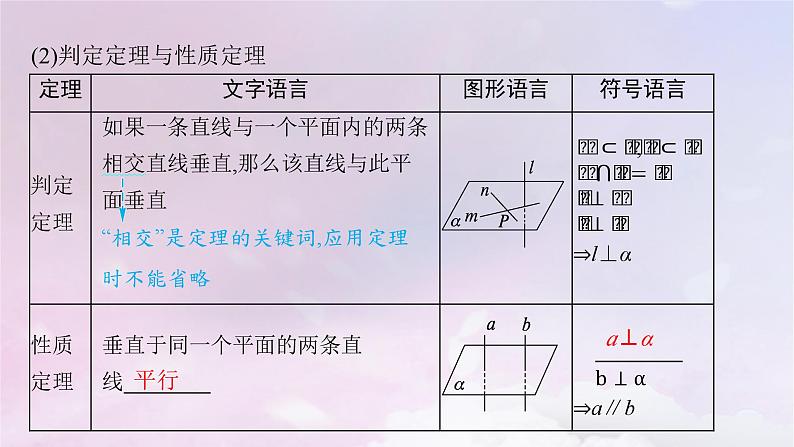
(2)判定定理与性质定理
(3)直线和平面所成的角①定义:平面的一条斜线和它在平面上的　　　　所成的角,叫做这条直线和这个平面所成的角. ②范围:[0°,90°],一条直线垂直于平面,它们所成的角是90°;一条直线和平面平行,或在平面内,它们所成的角是0°.
微思考空间中任意一直线m,在平面α内是否存在无数条直线与m垂直?
提示 存在,如图.
3.平面与平面垂直(1)二面角:从一条直线出发的两个　　　　　　所组成的图形叫做二面角. (2)二面角的平面角:如图,在二面角α-l-β的棱l上任取一点O,以该点为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,这两条射线所构成的∠AOB叫做二面角的平面角.二面角的平面角α的取值范围是[0°,180°].
(3)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是　　　　　　　,就说这两个平面互相垂直. 
(4)判定定理与性质定理
微点拨面面垂直的性质定理是作辅助线的一个重要依据.我们要作一个平面的一条垂线,通常是先找这个平面的一个垂面,在这个垂面中,作交线的垂线即可.
微思考若平面α⊥β,且α∩β=l,若直线m⊥l,则m与平面β一定垂直吗?
提示 不一定.当m⊂α时,m⊥β.
常用结论直线与平面垂直的五个结论(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线.(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这条直线与另一个平面也垂直.(5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)已知直线a,b,c,若a⊥b,b⊥c,则a∥c.(　　)(2)设m,n是两条不同的直线,α是一个平面,若m∥n,m⊥α,则n⊥α.(　　)(3)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.(　　)(4)若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β.(　　)
2.(2023山东泰安一模)已知m,n是两条不重合的直线,α是一个平面,n⊂α,则“m⊥α”是“m⊥n”的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
解析由线面垂直的性质定理知,若m⊥α,n⊂α,则m⊥n成立,即充分性成立;由线面垂直的判定定理,当m垂直平面α内的两条相交直线,才有m⊥α,即必要性不成立.故选A.
3.已知直线a和平面α,β,若α⊥β,a⊥β,则a与α的位置关系为　　　　　. 
答案 a∥α或a⊂α　解析 当a⊂α且a垂直于α,β的交线时,满足已知条件;当a∥α时也满足已知条件
典例突破例1.(1)(多选)已知a,b表示两条不同的直线,α,β表示两个不同的平面,下列说法正确的是(　　)A.若a⊥α,b⊥β,α∥β,则a∥bB.若a⊥α,b⊥β,a⊥b,则α⊥βC.若a⊥α,a⊥b,α∥β,则b∥βD.若α∩β=a,a∥b,则b∥α或b∥β
(2)(多选)如图所示,已知四边形ABCD是由一个等腰直角三角形ABC和一个有一内角为30°的直角三角形ACD拼接而成,将△ACD绕AC边旋转的过程中,下列结论可能成立的是(　　)A.CD⊥ABB.BC⊥ADC.BD⊥ABD.BC⊥CD
答案 (1)ABD　(2)ACD　
解析 (1)对于A,若a⊥α,α∥β,则a⊥β.又b⊥β,所以a∥b,故A正确;对于B,若a⊥α,a⊥b,则b⊂α或b∥α,所以存在直线m⊂α,使得m∥b.又b⊥β,所以m⊥β,所以α⊥β.故B正确;对于C,若a⊥α,a⊥b,则b⊂α或b∥α.又α∥β,所以b⊂β或b∥β,故C错误;对于D,若α∩β=a,a∥b,则b∥α或b∥β,故D正确.故选ABD.
(2)当将△ACD绕AC边旋转到CD⊥BC时,因为CD⊥AC,AC∩BC=C,此时CD⊥平面ABC,而AB,BC⊂平面ABC,则CD⊥AB,CD⊥BC,A,D正确;此时AB⊥平面BCD,DB⊂平面BCD,所以AB⊥DB,C正确;若BC⊥AD,而AB⊥BC,AB∩AD=A,故必有BC⊥平面ABD,由图形可知,D点在B点正上方,而CD