2025届高考数学一轮总复习第八章立体几何与空间向量第五节空间向量及其运算课件

这是一份2025届高考数学一轮总复习第八章立体几何与空间向量第五节空间向量及其运算课件，共47页。PPT课件主要包含了强基础增分策略，平行或重合，∠AOB，答案BCD，答案B，增素能精准突破，典例突破，答案A，答案1B，答案AB等内容，欢迎下载使用。
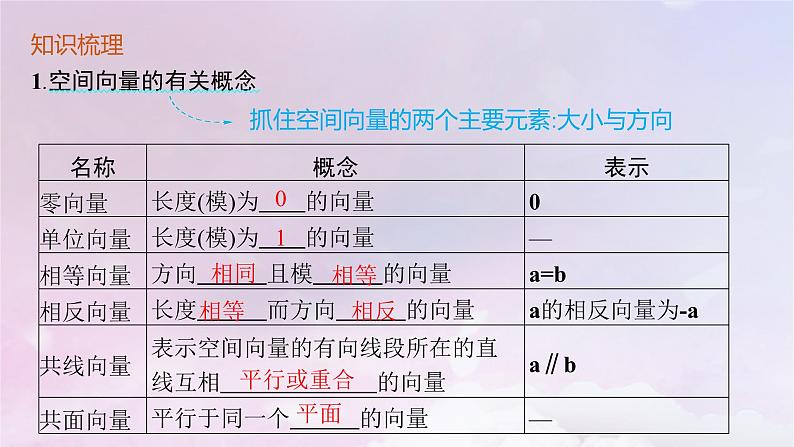
知识梳理1.空间向量的有关概念
抓住空间向量的两个主要元素:大小与方向
微点拨空间向量是由平面向量拓展而来的,因此空间向量的概念和性质与平面向量的概念和性质相同或相似.在学习空间向量时,与平面向量的相关内容相类比进行学习,将达到事半功倍的效果.
微思考“空间中任何两个向量都是共面向量”,这个结论是否正确?
提示 正确.根据向量相等的定义,可以把向量进行平移,空间任意两个向量都可以平移到同一个平面内,成为共面向量.
2.空间向量中的有关定理
微点拨1.利用向量的线性运算和空间向量基本定理表示向量是向量应用的基础.2.利用共线向量定理、共面向量定理可以证明一些平行、共面问题.
微思考基向量和基底一样吗?0是否能作为基向量?
提示 不一样.基底是指一个向量组,基向量是基底中的某一个向量;因为0与其他两个非零向量共面,所以0不能作为基向量.
3.空间向量的数量积(1)两向量的夹角①已知两个非零向量a,b,在空间任取一点O,作 =a, =b,则　　 　　叫做向量a,b的夹角,记作. 
(1)两个向量有相同的起点;(2)向量的方向
②范围:0≤≤π.(2)两个非零向量a,b的数量积:a·b=　　　　　　　　. 
|a||b|cs
微点拨向量的数量积满足交换律、分配律,但不满足结合律,即a·b=b·a,(a+b)·c=a·c+b·c成立,(a·b)·c=a·(b·c)不一定成立.
4.空间向量的坐标表示设a=(a1,a2,a3),b=(b1,b2,b3).
垂直问题一般通过向量的数量积运算来解决
a1b1+a2b2+a3b3
a1=λb1,a2=λb2,a3=λb3
a1b1+a2b2+a3b3=0
常用结论1.证明空间任意三点共线的方法对空间三点P,A,B可通过证明下列结论成立来证明三点共线:
2.证明空间四点共面的方法对空间四点P,M,A,B,除空间向量基本定理外,也可通过证明下列结论成立来证明共面:
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)空间中模相等的两个向量方向相同或相反.(　　) (2)空间中任意两非零向量a,b共面.(　　)(3)对于空间非零向量a,b,若a·b