2025届高考数学一轮总复习第九章平面解析几何指点迷津十课件

这是一份2025届高考数学一轮总复习第九章平面解析几何指点迷津十课件，共23页。PPT课件主要包含了技巧一灵活运用定义，答案D等内容，欢迎下载使用。

解析几何减少运算量的常用技巧很多同学厌烦解析几何题目,是因为运算量过大.尤其在考试过程中,要想在规定时间内完成解答,计算能力是一个重要的因素.下面介绍四种减少计算量的技巧.
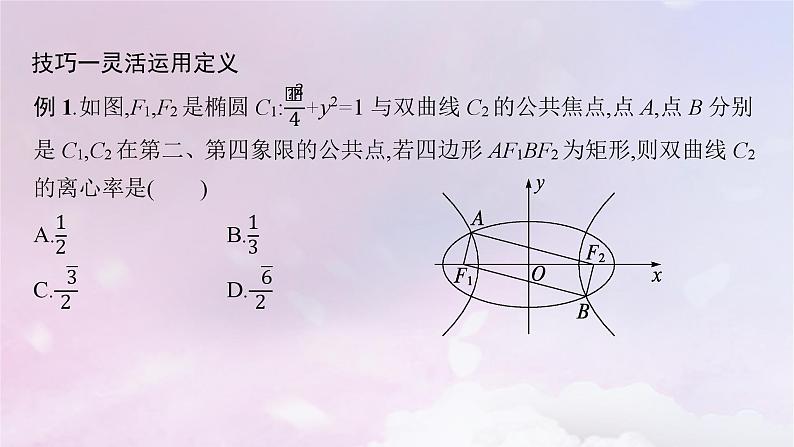
解析 设|AF1|=x,|AF2|=y,y>x.
故|AF1|+|AF2|=2a=4,即x+y=4.①又四边形AF1BF2为矩形,故|AF1|2+|AF2|2=|F1F2|2,即x2+y2=(2c)2=12.②
名师点析解决此类问题要熟练掌握平面几何的性质,数形结合,灵活运用定义,往往能达到化难为易、化繁为简、事半功倍的效果.
技巧二设而不求,整体代换
名师点析运用“设而不求”方法的两点技巧
技巧三巧用“根与系数的关系”,化繁为简
(1)求椭圆E的方程;(2)过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N.当|MN|=2时,求k的值.
(2)设过点P(-2,1),斜率是k的直线为l,直线l的方程为y-1=k(x+2),联立直线l和椭圆E的方程,
消去y,整理得(1+4k2)x2+(16k2+8k)x+16k2+16k=0.
由Δ>0可得(16k2+8k)2-4×(1+4k2)(16k2+16k)>0,解得k<0.设B(x1,y1),C(x2,y2),
名师点析在圆锥曲线问题中,常设出直线与圆锥曲线的两个交点坐标,联立直线方程与圆锥曲线方程,消元得到一元二次方程,利用根与系数的关系,得到两个交点横坐标或纵坐标的关系,这是解决圆锥曲线问题的常用方法.通过设而不求,大大降低了运算量,体现了整体思想.
技巧四 圆锥曲线的弦长公式化为快速求圆锥曲线的弦长,我们推出一般形式下直线与椭圆、双曲线相交的过程性结论,把结论当成公式运用,能达到事半功倍的效果.
(1)(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0;(2)Δ=4a2b2(b2+a2k2-m2);
结论3:直线与双曲线相交的四条结论只需把椭圆四条结论中的b2换成-b2即可.例如:
结论4:直线与焦点在y轴上的椭圆或双曲线的结论,只需将四条结论中的a2,b2互换.
【结论应用】例4.已知椭圆E: =1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.(1)当t=4,|AM|=|AN|时,求△AMN的面积;(2)当2|AM|=|AN|时,求k的取值范围.
解(1)设M(x1,y1),则由题意知y1>0.由已知及椭圆的对称性,知直线AM的倾