2025届高考数学一轮总复习第九章平面解析几何高考解答题专项五第一课时定点与定值问题课件

这是一份2025届高考数学一轮总复习第九章平面解析几何高考解答题专项五第一课时定点与定值问题课件，共44页。
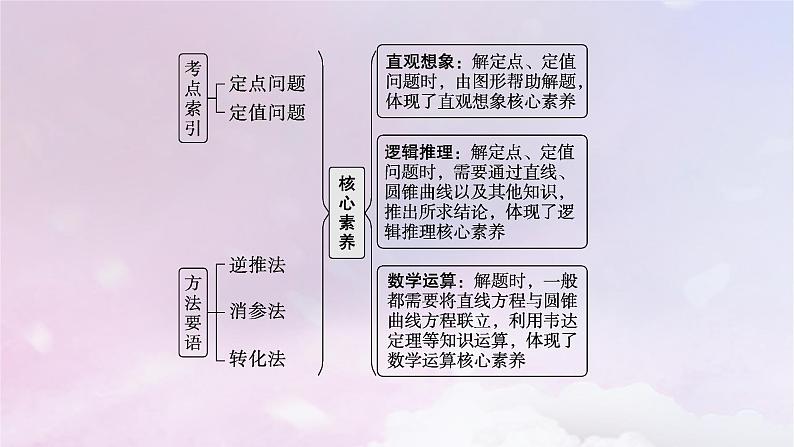
圆锥曲线中的综合问题考情分析从近两年的高考试题来看,解析几何是高考的重点,约占整个试卷的15%,通常以一大两小的模式命题.我们发现对解析几何大题的考查,考题一般放在第21题的位置,相应的题目难度有所下降,所以说解析几何大题是学生必须得高分甚至是满分的题目.
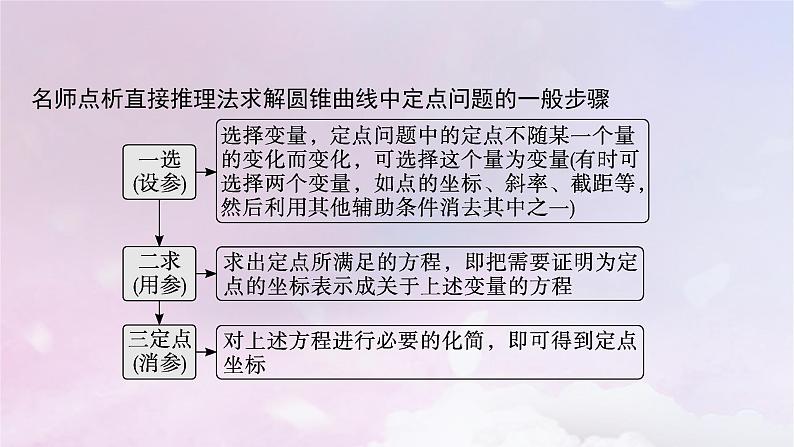
考向1.直接推理法求解圆锥曲线中定点问题
A(-2,0)在C上.(1)求C的方程;(2)过点(-2,3)的直线交C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明:线段MN的中点为定点.
(2)证明根据题意,直线PQ的斜率存在,设MN的中点为T,直线PQ的方程为y=k(x+2)+3(k0.
考向2.逆推法求圆锥曲线中的定点问题例2.已知抛物线C的方程y2=2px(p>0),焦点为F,点P在抛物线C上,且点P到点F的距离比它到y轴的距离大1.(1)试求出抛物线C的方程.(2)若抛物线C上存在两动点M,N(M,N在对称轴两侧),满足OM⊥ON(O为坐标原点),过点F作直线交抛物线C于A,B两点,若AB∥MN,则线段MN上是否存在定点E,使得 =4恒成立?若存在,请求出点E的坐标;若不存在,请说明理由.
若直线AB斜率不存在,则|AB|=4,|EM||EN|=4×4=16,此时点E(4,0)满足题意.综上所述,定点E为(4,0).
方法总结由特殊到一般法求定点问题的方法由特殊到一般法求解定点问题时,常根据动点或动直线的特殊情况探索出定点,再证明该定点与变量无关.
(1)求椭圆C的方程;(2)过点F1(-1,0)作动直线l与椭圆交于A,B两点,过点A作直线x=-4的垂线,垂足为N,求证:直线BN过定点.
考向1.直接消参法求圆锥曲线中定值问题
(1)求C的方程;(2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,M在第二象限,直线MA1与直线NA2交于P,证明:点P在定直线上.
(2)证明(方法1)(ⅰ)当直线MN的斜率存在时,设直线MN的方程为y=k(x+4),设M(x1,y1),N(x2,y2),y1>0.
∴当直线MN的斜率存在时,点P在定直线x=-1上.
(方法2)由于直线MN与双曲线左支交于M,N两点,∴直线MN的斜率不为0.
又A1(-2,0),A2(2,0),易知x1≠-2,x2≠2,∴直线A1M,直线A2N的方程分别为
名师点析直接消参法求圆锥曲线中定值问题的一般步骤
对点训练3已知双曲线C: =1(a>0,b>0)的虚轴长为4,直线2x-y=0为双曲线C的一条渐近线.(1)求双曲线C的标准方程;(2)记双曲线C的左、右顶点分别为点A,点B,过点T(2,0)的直线l与双曲线交于M,N两点,直线MA交y轴于点P,直线NB交y轴于点Q,记△PAT面积为S1,△QBT面积为S2,求证: 为定值.
(2)证明由题可知A(-1,0),B(1,0).设直线l:x=ny+2,M(x1,y1),N(x2,y2).把直线方程代入双曲线方程得(4n2-1)y2+16ny+12=0.由题可知4n2-1≠0,Δ>0,
考向2.特殊转化法求圆锥曲线中的定值问题
(2)存在,m=-1.理由如下.
方法总结由特殊到一般法求定值问题的两个常用技巧
点B分别为椭圆C的右顶点和上顶点,点P在椭圆C上且不与四个顶点重合.(1)求椭圆C的标准方程;(2)若直线PA与y轴交于点N,直线PB与x轴交于点M,则|AM||BN|是否为定值?若为定值,请求出该定值;若不为定值,请说明理由.
(2)|AM||BN|为定值.理由如下.∵点P不与四个顶点重合,∴直线PA,PB的斜率存在且不为0.