2025届高考数学一轮总复习第十一章计数原理概率随机变量及其分布第三节二项式定理课件

这是一份2025届高考数学一轮总复习第十一章计数原理概率随机变量及其分布第三节二项式定理课件，共40页。PPT课件主要包含了内容索引，强基础增分策略，增素能精准突破，常用结论，答案B，答案A，典例突破等内容，欢迎下载使用。
知识梳理1.二项式定理
(1)二项式定理:(a+b)n=　　　　　　　　　　　　　　　　　　,n∈N*. (2)通项:　　　　 　　　,它表示展开式的第k+1项. (3)二项式系数:二项展开式中各项的系数 (k=0,1,2,…,n)叫做二项式系数.
字母a,b是一种“符号”,实际上可以是数和式
只与各项的项数有关,而与a,b的值无关
微点拨二项式系数 (k=0,1,2,…,n)是组合数,它与二项展开式中对应项的系数不一定相等,应注意区分二项式系数与项的系数这两个不同的概念.项的系数是指该项中除变量外的常数部分,它不仅与各项的项数有关,而且也与a,b的值有关.如(a+bx)n的展开式中,第k+1项的二项式系数是 ,而该项的系数是 an-kbk.当然,在某些二项展开式中,各项的系数与二项式系数是相等的.
微思考(a+b)n与(b+a)n的展开式有何区别与联系?
提示 (a+b)n的展开式与(b+a)n的展开式的项完全相同,但对应的项不相同,两个展开式的通项不同.
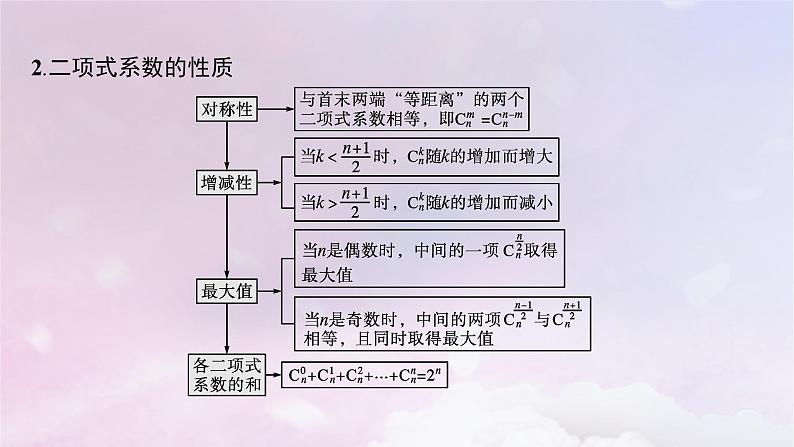
2.二项式系数的性质
微点拨利用赋值法求二项式系数的和.
微思考二项展开式中二项式系数最大时该项的系数就最大吗?
提示 不一定最大.当二项式中a,b的系数为1时,二项式系数等于项的系数,则二项式系数最大时,该项的系数就最大,否则不一定.
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)(a+b)n的展开式中的第k项是 an-kbk.(　　)(2)在二项展开式中,系数最大的项为中间的一项或中间的两项.(　　)(3)通项Tk+1= an-kbk中的a和b不能互换.(　　)(4)在(a+b)n的展开式中,某项的系数与该项的二项式系数相同.(　　)
2.在(1+2x)5的展开式中,x2的系数等于(　　)A.80B.40C.20D.10
3.若 的展开式中第3项的二项式系数是15,则展开式中所有项的系数之和为　　　　　. 
考向1.二项展开式中的特定项(或系数)典例突破
(3)二项式 的展开式中的常数项为15,则实数a=　　　　　. 
例1.(1)(2023天津,11)在(2x3- )6的展开式中含x2的项的系数为　　　　　. (2)设i为虚数单位,则(x+i)6的展开式中含x4的项为　　　　　. 
答案 (1) 60　(2)-15x4　(3)3　
方法归纳求二项展开式中特定项的步骤
对点训练1(1) 的展开式中常数项为(　　)A.-15B.-20C.15D.20
(2)(2023山东泰安一模)若 的展开式中含x6的项的系数是-16,则实数a的值是(　　)A.-2B.-1C.1D.2
答案 (1)B　(2)D　
考向2.已知两个因式之积求其特定项(或系数)典例突破
答案 (1)D　(2)28　
方法总结求两个因式之积的特定项(或系数)的两种常用方法
对点训练2(1)(2023辽宁沈阳三模) 的展开式中,含x-2的项的系数为(　　)A.430D.240(2)(2-x)(2x+1)6的展开式中含x4的项的系数为　　　　　. 
答案 (1)B　(2)320　
考向3.已知三项式求其特定项(或系数)典例突破例3.(1)(x2+3x-1)5展开式中含x的项的系数为(　　)A.-3B.3C.-15D.15
方法总结求三项展开式中某些特定项(或系数)的三种方法
对点训练3在(x2-2x+y)6的展开式中,含x5y2的项的系数为(　　)A.-480B.480C.-240D.240
解析 (x2-2x+y)6看成是6个(x2-2x+y)相乘,要得到x5y2,需要“从6个因式中,2个因式取y,1个因式取x2,3个因式取-2x”,此时含x5y2的的项系数为
例4.(1)(多选)在 的展开式中,各项系数和与二项式系数和之和为128,则(　　)A.二项式系数和为64B.各项系数和为64C.常数项为-135 D.常数项为135(2)若(1-2x)8=a0+a1x+a2x2+…+a8x8,则|a0|+|a1|+|a2|+|a3|+…+|a8|=(　　)A.28-1D.38
答案 (1)ABD　(2)D　
(2)由题可知,x的奇数次幂的系数均为负数,所以|a0|+|a1|+|a2|+|a3|+…+|a8|=a0-a1+a2-a3+…+a8.因为(1-2x)8=a0+a1x+a2x2+…+a8x8,令x=-1得a0-a1+a2-a3+…+a8=38,则|a0|+|a1|+|a2|+|a3|+…+|a8|=38.故选D.
名师点析形如(ax+b)n,(ax2+bx+c)m(a,b,c∈R)的式子,求其展开式的各项系数之和,常用赋值法.
(2)已知二项式 的展开式的二项式系数和为64,则展开式中的有理项系数和为　　　　　. 
对点训练4(1)(2023北京大兴校考三模)若(1-x)5=a0+a1x+a2x2+…+a5x5,则|a0|+|a1|+|a2|+…+|a5|=　　　. 
答案 (1)32　(2)65　
所以|a0|+|a1|+|a2|+…+|a5|=a0-a1+a2-a3+a4-a5.令x=-1,可得25=a0-a1+a2-a3+a4-a5=32.(2)因为展开式的二项式系数和为64,所以2n=64,
(2) 的展开式中各项系数的和为-1,则该展开式中系数最大的项为　　　　　　　　　. 
例5.(1)(多选)(2023山东青岛一模)在 的展开式中,下列说法正确的是(　　)A.常数项是1 120B.第四项和第六项的系数相等C.各项的二项式系数之和为256D.各项的系数之和为256
答案 (1) AC　(2)80x-3　
方法总结1.二项式系数最大项的确定方法
2.二项展开式系数最大项的求法
(2)已知( +3x2)n的展开式中,各项系数和比它的二项式系数和大992,则展开式中系数最大的项为　　　　　. 
对点训练5(1)(多选)已知 的展开式共有13项,则下列说法中正确的有(　　)A.所有奇数项的二项式系数和为212B.所有项的系数和为312C.二项式系数最大的项为第6项或第7项D.有理项共5项
解析 (1)因为n+1=13,所以n=12.所有奇数项的二项式系数和为211,故A错误;令x=1,得所有项的系数和为312,故B正确;由二项式系数的性质,可知二项式系数最大的项为第7项,故C错误;