




还剩8页未读,
继续阅读
成套系列资料,整套一键下载
- 高中数学3.3.2抛物线的几何性质1课件2023-2024学年苏教版选择性必修第一册 课件 0 次下载
- 高中数学3.3.2抛物线的几何性质2课件2023-2024学年苏教版选择性必修第一册 课件 0 次下载
- 高中数学4.1数列1课件2023-2024学年苏教版选择性必修第一册 课件 0 次下载
- 高中数学4.2.1等差数列的概念课件2023-2024学年苏教版选择性必修第一册 课件 0 次下载
- 高中数学4.3.3等比数列的前n项和1课件2023-2024学年苏教版选择性必修第一册 课件 0 次下载
- 高中数学5.1.2瞬时变化率__导数1课件2023-2024学年苏教版选择性必修第一册 课件 0 次下载
苏教版 (2019)选择性必修第一册第3章 圆锥曲线与方程3.2 双曲线课堂教学课件ppt
展开
这是一份苏教版 (2019)选择性必修第一册第3章 圆锥曲线与方程3.2 双曲线课堂教学课件ppt,共15页。PPT课件主要包含了复习引入,-xy,数学建构,-x-y,x-y,渐近线,慢慢靠近,动画演示,离心率,1定义等内容,欢迎下载使用。
1.双曲线的定义是怎样的? 2.双曲线的标准方程是怎样的?
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
F (±c,0) F(0,± c)
思考回顾椭圆的简单几何性质?
①范围; ②对称性; ③顶点;④离心率等.
双曲线是否具有类似的性质呢?
回想:我们是怎样研究上述性质的?
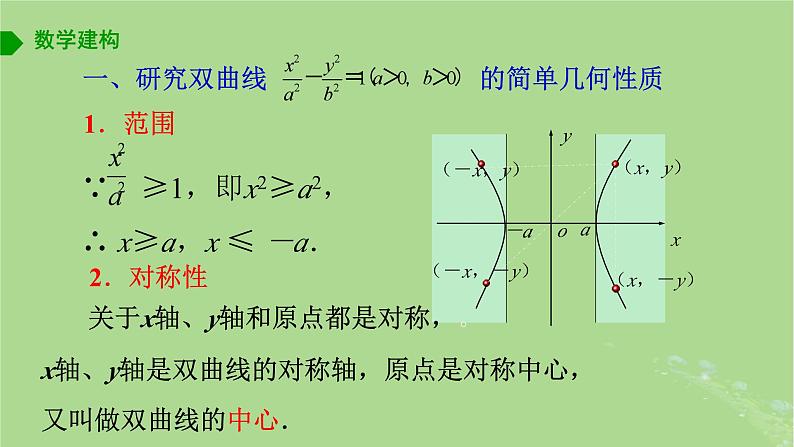
2.对称性
关于x轴、y轴和原点都是对称,。
x轴、y轴是双曲线的对称轴,原点是对称中心,又叫做双曲线的中心.
∵ ≥1,即x2≥a2,∴ x≥a,x ≤ -a.
(1)双曲线与对称轴的交点,叫做双曲线的顶点.
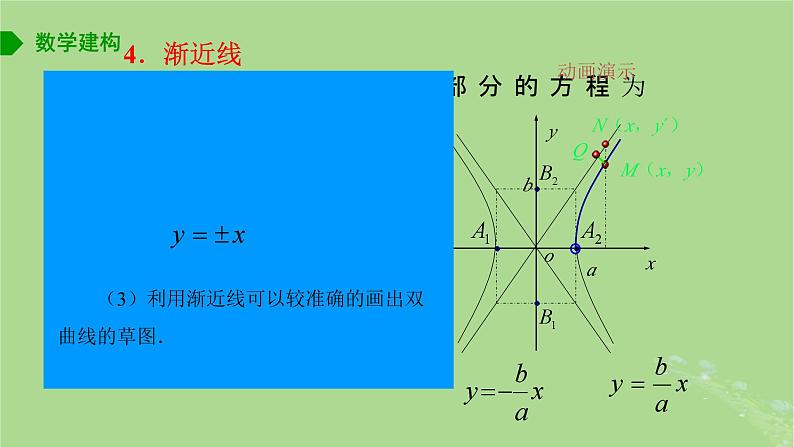
(2)如图,线段A1 A2叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段B1 B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
顶点是A1(-a,0),A2(a,0).
e是表示双曲线开口大小的一个量,e越大开口越大.
(4)等轴双曲线的离心率e= ?
(1)范围:y≥a,y≤-a.
关于坐标轴和原点都对称
例1 求双曲线 的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程.
问:若将题目中“焦点在 y 轴上”改为“焦点在坐标轴上”呢?
例2 已知双曲线的中心在原点,焦点在y轴上,焦距为16,离心率为 ,求双曲线的标准方程.
1.双曲线的定义是怎样的? 2.双曲线的标准方程是怎样的?
| |MF1|-|MF2| | =2a(0<2a<|F1F2|)
F (±c,0) F(0,± c)
思考回顾椭圆的简单几何性质?
①范围; ②对称性; ③顶点;④离心率等.
双曲线是否具有类似的性质呢?
回想:我们是怎样研究上述性质的?
2.对称性
关于x轴、y轴和原点都是对称,。
x轴、y轴是双曲线的对称轴,原点是对称中心,又叫做双曲线的中心.
∵ ≥1,即x2≥a2,∴ x≥a,x ≤ -a.
(1)双曲线与对称轴的交点,叫做双曲线的顶点.
(2)如图,线段A1 A2叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段B1 B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
顶点是A1(-a,0),A2(a,0).
e是表示双曲线开口大小的一个量,e越大开口越大.
(4)等轴双曲线的离心率e= ?
(1)范围:y≥a,y≤-a.
关于坐标轴和原点都对称
例1 求双曲线 的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程.
问:若将题目中“焦点在 y 轴上”改为“焦点在坐标轴上”呢?
例2 已知双曲线的中心在原点,焦点在y轴上,焦距为16,离心率为 ,求双曲线的标准方程.













