吉林省松原市乾安县2023届九年级下学期一模测试数学试卷(含解析)

这是一份吉林省松原市乾安县2023届九年级下学期一模测试数学试卷(含解析)，共23页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1. -17的相反数是( )
A. 17B. -17C. 7D. -7
2. 我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球，结束了183天的在轨飞行时间.从2003年神舟五号载人飞船上天以来，我国已有13位航天员出征太空，绕地球飞行共约2.3亿公里.将数据232000000用科学记数法表示为( )
A. ×109B. 2.32×109C. ×108D. 23.2×108
3. 不等式2x+3<5的解集在数轴上表示为( )
A. B. C. D.
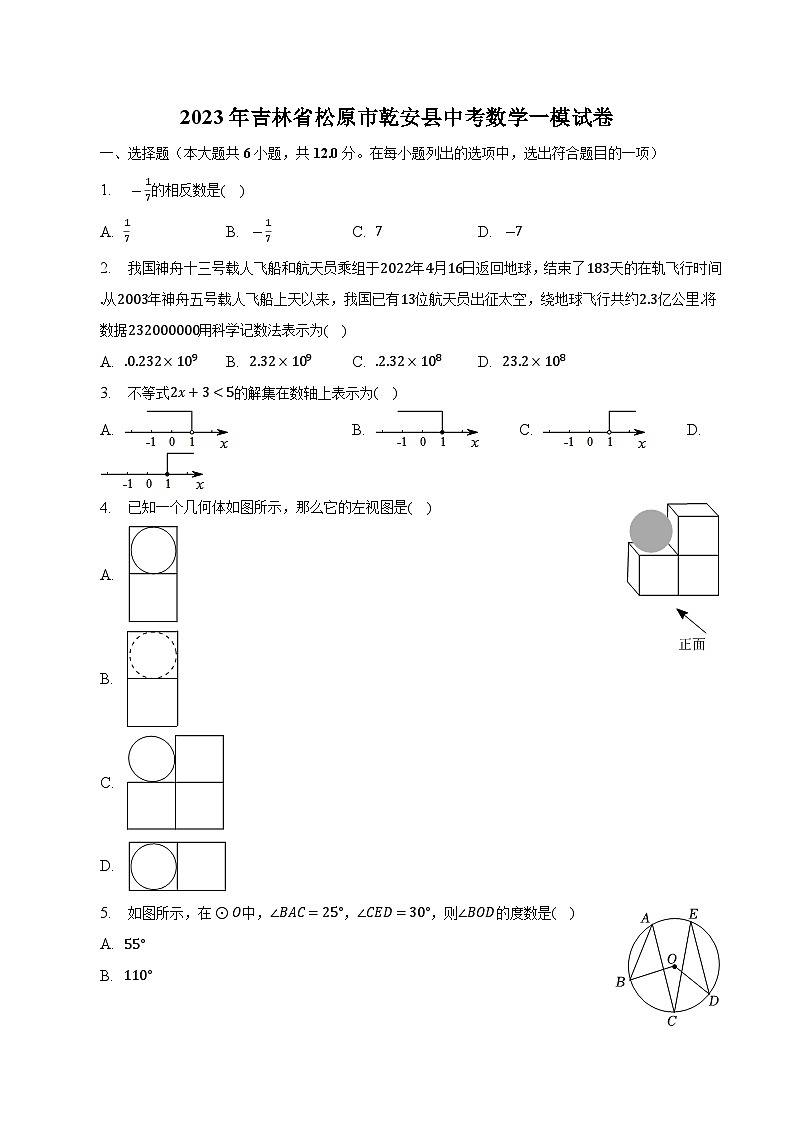
4. 已知一个几何体如图所示，那么它的左视图是( )
A.
B.
C.
D.
5. 如图所示，在⊙O中，∠BAC=25°，∠CED=30°，则∠BOD的度数是( )
A. 55°
B. 110°
C. 125°
D. 150°
6. 我国明代数学读本《算法统宗》中有一道题，其题意为：客人一起分银子，若每人7两，还剩4两；若每人9两，还差8两.问银子共有几两？设银子共有x两，则可列方程为( )
A. 7x+4=9x-8B. 7x-4=9x+8C. x+47=x-89D. x-47=x+89
二、填空题（本大题共8小题，共24.0分）
7. 计算3 2- 2的结果是______．
8. 分解因式：a2-25= ．
9. 计算：a2b2÷a2a2= ______ ．
10. 若关于x的方程x2-6x+c=0有两个相等的实数根，则c的值为______．
11. 如图所示，分别以线段AB的端点A和B为圆心，大于12AB的长为半径作弧，连接两弧交点，得直线l，在直线l上取一点C，使得∠CBA=25°，延长AC至M，∠BCM的度数为______ ．
12. 长方形ABCD在平面直角坐标系中的位置如图所示，若AD=10，点B的坐标为(-6,6)，则点C的坐标为______ ．
13. 如图，在河两岸分别有A、B两村，现测得三点A、B、D在一条直线上，A、C、E在一条直线上，若BC//DE，DE=90米，BC=70米，BD=20米，那么A、B两村间的距离为______米．
14. 如图所示，矩形ABCD的对角线AC，BD交于点O，分别以点A，C为圆心，AO长为半径画弧，分别交AB，CD于点E，F.若BD=6，∠CBA=30°，则图中阴影部分的面积为______ .(结果保留π)
三、计算题（本大题共1小题，共5.0分）
15. 先化简，再求值：x(x-2)-(x+1)(x-1)，其中x=10．
四、解答题（本大题共11小题，共79.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题5.0分)
某鞋店有A、B、C、D四款运动鞋，元旦期间搞“买一送一”促销活动，用树状图或表格求随机选取两款不同的运动鞋，恰好选中A、C两款的概率．
17. (本小题5.0分)
如图，已知：AC=BD，∠A=∠B，∠E=∠F，求证：AE=BF．
18. (本小题5.0分)
我们把顶点都在格点上的四边形叫做格点四边形.如图，在4×4的方格纸中，有格点线段AB，AC，BC，请按要求画出格点四边形．
(1)在图1中画格点四边形ABCD，使其为中心对称图形．
(2)在图2中画格点四边形ABCE，使得对角互补．
19. (本小题7.0分)
列分式方程解应用题：
2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢．某工厂为了满足市场需求，提高生产效率，在生产操作中需要用机器人来搬运原材料．现有A、B两种机器人，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运750kg所用时间与B型机器人搬运500kg所用时间相等，则两种机器人每小时分别搬运多少原料？
20. (本小题7.0分)
李老师把油箱加满油后驾驶汽车从县城到省城接客人，油箱加满后，汽车行驶的总路程y(单位：km)与平均耗油量x(单位：L/km)之间的关系如图所示．
(1)求y与x的函数关系式．
(2)当平均耗油量为0.16L/km时，汽车行驶的总路程为多少km？
21. (本小题7.0分)
如图，某无人机兴趣小组在操场上开展活动，此时无人机在离地面30米的D处，无人机测得操控者A的俯角为30°，测得教学楼BC顶端点C处的俯角为45°.又经过人工测量测得操控者A和教学楼BC之间的距离为57米．求教学楼BC的高度．(点A，B，C，D都在同一平面上，结果保留根号)
22. (本小题7.0分)
为了解某校八年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制出统计图1和图2，请根据相关信息，解答下列问题：

(1)本次抽测的男生人数为______ ，图1中m的值为______ ；
(2)本次抽测的这组数据的平均数为______ 次，众数为______ 次；
(3)若规定引体向上5次以上(含5次)为体能达标，根据样本数据，估计该校350名八年级男生中有多少人体能达标．
23. (本小题8.0分)
杆秤是我国传统的计重工具，如图，秤钩上所挂的不同重量的物体使得秤砣到秤纽的水平距离不同．称重时，秤钩所挂物重为x(斤)时，秤杆上秤砣到秤纽的水平距离为y(厘米).如表中为若干次称重时所记录的一些数据，且y是x的一次函数．
注：秤杆上秤砣在秤纽左侧时，水平距离y(厘米)为正，在右侧时为负．
(1)根据题意，完成上表；
(2)请求出y与x的关系式；
(3)当秤杆上秤砣到秤纽的水平距离为15厘米时，秤钩所挂物重是多少斤？
24. (本小题8.0分)
如图，在等腰△ABC中，∠BAC=90°，点D为直线BC上一动点(点D不与B、C重合).以AD为边向右侧作正方形ADEF，连接CF．
【猜想】如图①，当点D在线段BC上时，直接写出CF、BC、CD三条线段的数量关系．
【探究】如图②，当点D在线段BC的延长线上时，判断CF、BC、CD三条线段的数量关系，并说明理由．
【应用】如图③，当点D在线段BC的反向延长线上时，点A、F分别在直线BC两侧，AE、DF交点为点O连接CO，若AB= 2，CF=1，则CO= ______ ．
25. (本小题10.0分)
如图所示，在Rt△ABC中，∠ABC=90°，AB=4，BC=2.点P在AC上从点A以每秒 5个单位长度的速度向终点C运动.点Q从点B沿BA方向以每秒1个单位长度的速度运动，当点P不与点A重合时，连接PQ，以PQ，BQ为邻边作▱PQBM.当点P停止运动时，点Q也随之停止运动，设点P的运动时间t(s)，▱PQBM与△ABC重叠部分的图形面积为S．
(1)点P到边AB的距离为______ ，点P到BC边的距离为______ ；(用含t的代数式表示)
(2)当点M落在线段BC上时，求t的值；
(3)求S与t之间的函数关系式，并写出自变量t的取值范围．
26. (本小题10.0分)
如图①，在平面直角坐标系中，平行于x轴的直线与抛物线y=ax2(a>0)相交于A、B两点，设点B的横坐标为m(m>0)．
(1)求AB的长(用含m的代数式表示)．
(2)如图②，点C在直线AB上，点C的横坐标为2m，若a=1，m=2，求顶点在x轴上且经过B、C两点的抛物线的顶点坐标．
(3)点D在直线AB上，BD=2AB，过O、B、D三点的抛物线的顶点为P，其对应哈数的二次项系数为a1．
①求a1a的值．
②当m=2，△BPD为等腰直角三角形时，直接写出a的值．
答案和解析
1.答案：A
解析：解：-17的相反数是17，
故选：A．
根据只有符号不同的两个数互为相反数，可得一个数的相反数．
本题考查了相反数，在一个数的前面加上负号就是这个数的相反数．
2.答案：C
解析：解：232000000=2.32×108．
故选：C．
用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|<10，n为整数，且n比原来的整数位数少1，据此判断即可．
本题主要考查了用科学记数法表示较大的数，掌握形式为a×10n，其中1≤|a|<10，确定a与n的值是解题的关键．
3.答案：A
解析：解：移项得，2x<5-3，
合并同类项得，2x<2，
系数化为1得，x<1．
在数轴上表示为：
．
故选：A．
先求出不等式的解集，再在数轴上表示出来即可．
本题考查的是在数轴上表示不等式的解集，熟知实心圆点与空心圆点的区别是解答此题的关键．
4.答案：A
解析：解：该几何体的左视图如下：

故选：A．
根据从左边看得到的图形是左视图，可得答案．
本题考查了简单组合体的三视图，从左边看得到的图形是左视图，注意中间看不到的线用虚线表示．
5.答案：B
解析：解：连接BE，
∵∠BEC=∠BAC=25°，∠CED=30°，
∴∠BED=∠BEC+∠CED=55°，
∴∠BOD=2∠BED=110°．
故选：B．
首先连接BE，由圆周角定理即可得∠BEC的度数，继而求得∠BED的度数，然后由圆周角定理，求得∠BOD的度数．
此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．
6.答案：D
解析：解：∵银子共有x两，每人7两，还剩4两，
∴分银子的人共x-47人；
∵银子共有x两，每人9两，还差8两，
∴分银子的人共x+89人．
又∵分银子的人数不变，
∴可列方程组x-47=x+89．
故选：D．
根据“每人7两，还剩4两；每人9两，还差8两”，结合分银子的人数不变，即可得出关于x的一元一次方程，此题得解．
本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．
7.答案：2 2
解析：解：原式=2 2．
故答案为：2 2．
直接利用二次根式的加减运算法则计算得出答案．
此题主要考查了二次根式的加减，正确掌握相关运算法则是解题关键．
8.答案：(a-5)(a+5)
解析：解：a2-25=(a-5)(a+5)．
故答案为：(a-5)(a+5)．
利用平方差公式分解即可求得答案．
本题考查了利用平方差公式分解因式的方法．题目比较简单，解题需细心．
9.答案：2ab
解析：解：a2b3÷a2b2
=a2b3⋅2b2a
=2ab，
故答案为：2ab．
根据分式的除法转化为乘法，再计算即可．
本题考查了分式的乘除法，解决本题的关键是掌握分式的乘除法的运算过程．
10.答案：9
解析：解：根据题意得△=(-6)2-4c=0，
解得c=9．
故答案为9．
根据判别式的意义得到△=(-6)2-4c=0，然后解关于c的一次方程即可．
本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系：当△>0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△<0时，方程无实数根．
11.答案：50°
解析：解：由作法得CN垂直平分AB，
∴CA=CB，
∴∠CAB=∠CBA=25°，
∴∠BCM=∠CAB+∠CBA=25°+25°=50°．
故答案为：50°．
利用作法得到CN垂直平分AB，再根据线段垂直平分线的性质得到CA=CB，然后根据等腰三角形的性质和三角形外角性质求∠BCM的度数．
本题考查了作图-复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质．
12.答案：(4,6)
解析：解：在长方形ABCD中，BC//AD，
∴点B与点C的纵坐标相等，
设点C(x,3)，
∵AD=10，
∴BC=10，
∴x=-6+10=4，
∴C(4,6)．
故答案为：(4,6)．
由题意易得BC//AD，则点B与点C的纵坐标相等，然后根据两点距离公式可进行求解．
本题主要考查坐标与图形性质，熟练掌握求一个点的坐标是解题的关键．
13.答案：70
解析：解：由题意可得，△ABC∽△ADE，
∴BCDE=ABAD，即7090=ABAB+20，解得AB=70米．
由BC//DE，可得，△ABC∽△ADE，进而利用对应边成比例求解线段的长度．
熟练掌握相似三角形的性质，能够求解一些简单的实际问题．
14.答案：32π
解析：解：∵四边形ABCD是矩形，
∴AC=BD=6，OA=OC=OB=OD，AB//CD，
∴OA=OC=3，∠ACD=∠CAB=30°，
∴图中阴影部分的面积为：2×30π×32360=32π，
故答案为：32π.
由图可知，阴影部分的面积是扇形AEO和扇形CFO的面积之和．
本题考查扇形面积的计算、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
15.答案：解：原式=x2-2x-x2+1=-2x+1，
当x=10时，原式=-2×10+1=-19．
解析：按单项式乘以单项式法则和平方差公式化简，然后把给定的值代入求值．
考查的是整式的混合运算，主要考查了公式法、单项式与多项式相乘以及合并同类项的知识点．
16.答案：解：画树状图得：

∵共有12种等可能的结果，恰好选中A、C两款的有2种情况，
∴恰好选中A、C两款的概率为：212=16．
解析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好选中A、C两款的情况，再利用概率公式求解即可求得答案．
此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
17.答案：证明：∵AC=BD，
∴AC+CD=DB+CD，
即AD=BC，
在△ADE和△BCF中，
∠A=∠B∠E=∠FAD=BC，
∴△ADE≌△BCF(AAS)，
∴AE=BF．
解析：证明△ADE≌△BCF(AAS)，由全等三角形的性质得出AE=BF．
本题考查了全等三角形的判定与性质，证明△ADE≌△BCF是解题的关键．
18.答案：(1)如图1，四边形ABCD即为所求；

(2)如图2，四边形ABCE即为所求．
解析：(1)根据中心对称图形的性质即可在图1中画格点四边形ABCD，使其为中心对称图形．
(2)在图2中画格点四边形ABCE，使得对角互补．
本题考查了作图-旋转变换，多边形，解决本题的关键是掌握旋转的性质．
19.答案：解：设B种机器人每小时搬运x kg原料，
则A种机器人每小时搬运(x+30)kg原料，
根据题意得：750x+30=500x，
解得：x=60，
经检验，x=60为原方程的解，且符合题意，
则x+30=90，
答：A种机器人每小时搬运90kg原料，B种机器人每小时搬运60kg原料．
解析：设B种机器人每小时搬运x kg原料，则A种机器人每小时搬运(x+30)kg原料，由题意：A型机器人搬运750kg所用时间与B型机器人搬运500kg所用时间相等，列出分式方程，解方程并检验即可．
本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．
20.答案：解：(1)设y与x的函数表达式为y=kx，
将点(0.1,700)代入，得k=0.1×700=70，
∴y与x的函数表达式为y=70x．
(2)当x=0.16时，y=700.16=437.5，
∴当平均耗油量为0.16L/km时，汽车行驶的总路程为437.5km．
解析：(1)结合反比例函数的图象，利用待定系数法即可求解；
(2)当x=0.16代入(1)求得的函数值即可．
本题考查了待定系数法求反比例函数解析式以及求函数值，正确地求得反比例函数解析式是解题的关键．
21.答案：解：过点D作DE⊥AB于点E，过点C作CF⊥DE于点F，如图所示：
则四边形BCFE是矩形，
由题意得：AB=57米，DE=30米，∠DAE=30°，∠DCF=45°，
在Rt△ADE中，∠AED=90°，AD=2DE=60米，
AE= AD2-DE2=30 3(米)，
∴BE=AB-AE=(57-30 3)米，
∵四边形BCFE是矩形，
∴CF=BE=(57-30 3)米，
在Rt△DCF中，∠DFC=90°，
∴∠CDF=∠DCF=45°，
∴DF=CF=(57-30 3)米，
∴BC=EF=30-57+30 3=(30 3-27)米，
答：教学楼BC的高度为(30 3-27)米．
解析：本题考查了解直角三角形的应用中的仰角俯角问题、矩形的判定与性质等知识；掌握仰角俯角定义是解题的关键．过点D作DE⊥AB于点E，过点C作CF⊥DE于点F，由题意得AB=57米，DE=30米，∠DAE=30°，∠DCF=45°，再由勾股定理求出AE的长，然后求出CF=BE=(57-30 3)米，进而可得教学楼BC的高度．
22.答案：50 28 5.16 5
解析：解：(1)本次抽测的男生人数为10÷20%=50(人)，
m%=1450×100%=28%，即m=28，
故答案为：50、28；
(2)平均数为3×4+4×10+5×16+6×14+7×650=5.16(次)，
众数为5次，
故答案为：5.16；5；
(3)16+14+650×350=252(人)，
答：估计该校350名八年级男生中有252人体能达标．
(1)根据4次的人数及其百分比可得总人数，用6次的人数除以总人数求得m即可；
(2)根据平均数、众数的定义求解可得；
(3)总人数乘以样本中5、6、7次人数之和占被调查人数的比例可得．
本题考查了条形统计图，平均数和众数，读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
23.答案：(1)1.50；11
(2)y=4x-2
(3)4.25斤．
解析：解：(1)由表格中的数据可得，
每增加1厘米，重物增加0.25斤，
故当y=4时，x=1.00+(4-2)×0.25=1.50，
当x=3.25时，y=7+(3.25-2.25)÷0.25=11，
故答案为：1.50，11；
(2)设y与x的关系式为y=kx+b，
∵点(0,-2)，(0.75,1)在该函数图象上，
∴b=-20.75k+b=1，
解得k=4b=-2，
即y与x的关系式为y=4x-2；
(3)(3)当y=15时，15=4x-2，
解得x=4.25，
即当秤杆上秤砣到秤纽的水平距离为15厘米时，秤钩所挂物重是4.25斤．
(1)根据表格中的数据，可以发现每增加1厘米，重物增加0.25斤，从而可以计算出当y=4对应的x的值和当x=3.25时对应的y的值；
(2)根据题意和表格中的数据，可以求出y与x的关系式；
(3)将y=15代入(2)中的关系式，即可得到当秤杆上秤砣到秤纽的水平距离为15厘米时，秤钩所挂物重是多少斤．
本题考查一次函数的应用，解答本题的关键是明确题意，列出相应的函数关系式．
24.答案： 102
解析：解：(1)CD=BC-CF．
∵AB=AC，∠BAC=90°，
∴∠ABC=∠ACB=45°，
∵四边形ADEF是正方形，
∴AD=AF，∠DAF=90°=∠BAC，
∴∠BAD=∠FAC，
在△BAD和△CAF中，
AB=AC∠BAD=∠CAFAD=AF，
∴△BAD≌△CAF(SAS)，
∴BD=CF，
∵CD=BC-BD，
∴CD=BC-CF，
(2)CF=BC+CD，
理由如下：∵∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∵四边形ADEF是正方形，
∴AD=AF，∠DAF=90°，
∵∠BAD=∠BAC+∠DAC，
∠CAF=∠DAF+∠DAC，
∴∠BAD=∠CAF，
在△BAD和△CAF中，
AB=AC∠BAD=∠CAFAD=AF，
∴△BAD≌△CAF(SAS)，
∴BD=CF，
∵BD=BC+CD，
∴CF=BC+CD；
(3)∵∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∵四边形ADEF是正方形，
∴AD=AF，∠DAF=90°，
∴∠BAC=∠DAF，
∴∠BAD=∠CAF，
在△BAD和△CAF中，
AB=AC∠BAD=∠CAFAD=AF，
∴△BAD≌△CAF(SAS)，
∴BD=CF，∠ACF=∠ABD=180°-45°=135°，
∠FCD=∠ACF-∠ACB=90°，
则△FCD为直角三角形，
∵AB= 2，
∴BC= 2AB=2，
∵CD=BC+BD，
∴CD=BC+CF=2+1=3，
∴DF= DC2+CF2= 32+12= 10，
∵正方形ADEF中，O为DF中点，
∴CO=12DF= 102，
故答案为： 102．
(1)由“SAS”可证△BAD≌△CAF，由全等三角形的性质可得BD=CF，可得出结论；
(2)由“SAS”可证△BAD≌△CAF，由全等三角形的性质可得BD=CF，可得出结论；
(3)由“SAS”可证△BAD≌△CAF，由全等三角形的性质可得BD=CF，∠ACF=∠ABD=180°-45°=135°，可证∠DCF=90°，由勾股定理和直角三角形的性质可得出结论．
本题是四边形综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，正方形的性质，直角三角形的性质等知识，灵活运用这些性质解决问题是本题的关键．
25.答案：t 4-2t
解析：解：(1)如图1，过点P作PE⊥AB，由题意可知AP= 5t，

∵∠B=90°，AB=4，BC=2，
∴AC= AB2+BC2=2 5，
∴cs∠A=2 55，sin∠A= 55，
∴PE=AP⋅sin∠A= 5t× 55=t，AE=AP⋅cs∠A= 5t×2 55=2t，
∴点P到AB的距离为t，点P到BC距离为4-2t；
故答案为：t；4-2t；
(2)如图2，当点M落在线段BC上时，

∵四边形PMBQ是平行四边形，
∴PM//BQ，PM⊥BC，
∴四边形PMBQ是矩形，
∴PQ⊥AB，
∴PQ=t，AQ=2t，
∵BQ=t，
∴AB=t+2t=4，
解得：t=43；
(3)①当0≤t≤43时，▱PQBM与△ABC重叠面积为S▱PQBM，如图1，

∴S=S▱PQBM=PE⋅BQ，
由(1)可知PE=t，BQ=t，
∴S=t2，
②当43则▱PQBM与△ABC重叠面积为S梯形PQBN，
∴S=S梯形PQBN=12×(PN+BQ)×PE，
∵PE=t，BQ=t，PN=4-2t，
∴S=12×(4-2t+t)×t=-12t2+2t，
综上所述，S=t2(0≤t≤43)-12t2+2t(43(1)过点P作PE⊥AB，根据勾股定理求出AC，运用三角函数得出cs∠A=2 55，sin∠A= 55，应用解直角三角形求出PE，AE即可；
(2)当点M落在线段BC上时，证明四边形PMBQ是矩形，从而得到AB=t+2t=4，求出t即可；
(3)分两种情况讨论：①当0≤t≤43时，▱PQBM与△ABC重叠面积为S▱PQBM，根据已有数据计算即可；②当4326.答案：解：(1)∵点B的横坐标为m，点A与点B关于y轴对称，
∴点A的横坐标为-m．
∴AB=m-(-m)=2m．
(2)∵点B和点C关于对称轴对称，
∴经过B、C且顶点在x轴上的抛物线的对称轴为x=32m.
∵m=2，
∴抛物线的对称轴为x=3．
∴经过B、C且顶点在x轴上抛物线的顶点坐标为(3,0)．
(3)①如图1所示：当点D在点B的右侧时．

∵点B的横坐标为m，AB=2m，BD=2AB，
∴BD=4m．
∴点D的横坐标为5m．
∴过点O、B、D三点的抛物线的对称轴为x=3m．
设过点O、B、D三点的抛物线的解析式为y=a1(x-3m)2+k．
将(0,0)代入得：k=-9a1m2．
∴抛物线的解析式为y=a1(x-3m)2-9a1m2．
∵点B为两抛物线的交点，
∴am2=a1(m-3m)2-9a1m2，整理得：(a+5a1)m2=0．
∵m≠0，
∴a+5a1=0，即a1a=-15．
如图2所示：当点D在点B左侧时．

∵点B的横坐标为m，AB=2m，BD=2AB，
∴BD=4m．
∴D的横坐标为-3m．
∴过点O、B、D三点的抛物线的对称轴为x=-m．
设过点O、B、D三点的抛物线的解析式为y=a1(x+m)2+k．
将(0,0)代入得：k=-a1m2．
∴抛物线的解析式为y=a1(x+m)2-a1m2．
∵点B为两抛物线的交点，
∴am2=a1(m+m)2-a1m2，整理得(3a1-a)m2=0．
∴a1a=13．
综上所述，a1a的值为-15或13．
②如图3所示：当点D在点B的右侧时．过点P作PF⊥x轴，交AB与点E．

设点B的横坐标为m，由①可知BD=4m，过点O、B、D三点的抛物线的解析式为y=a1(x+m)2-9a1m2．
∴PF=-9a1m2．
又∵EF=am2，
∴PE=-9a1m2-am2．
∵△BDP为等腰直角三角形，
∴PE=12BD，
∴-9a1m2-am2=4m．
又∵m=2，a1a=-15．
∴185a-2a=4，解得：a=45．
如图4所示：当点D在点B的左侧时，连结AP，交x轴与点E．

由①可知BD=4m，过点O、B、D三点的抛物线的解析式为y=a1(x+m)2-a1m2．
∴PE=a1m2．
又∵AE=am2，
∴AP=a1m2+am2．
∵△PBD为等腰直角三角形，
∴PA=12BD=2m，即a1m2+am2=2m．
∵m=2，a1a=13，
∴23a+2a=2，解得：a=34．
综上所述：a的值为34或54．
解析：(1)依据抛物线的对称性可求得点A的横坐标为-m，然后依据AB=xB-xA求解即可；
∴AB=m-(-m)=2m．
(2)先求得经过B、C且顶点在x轴上的抛物线的对称轴为x=32m，然后将m=2代入可求得顶点的横坐标，然后依据x轴上各点的纵坐标为0求解即可；
(3)①当点D在点B的右侧时．先用含m的式子表示点B、D的坐标，然后可得到抛物线的对称轴为x=3m，设过点O、B、D三点的抛物线的解析式为y=a1(x-3m)2+k.将(0,0)代入求得k的值，得到抛物线的解析式，然后依据B、D两点的纵坐标相等可得到关于a、a1的等式于是可求得a1a的值；同理可求得当点D在点B左侧时a1a的值；②当点D在点B的右侧时．过点P作PF⊥x轴，交AB与点E.先求得PE的长，然后依据PE=12BD列出关系式，然后将m=2，a1=-15a代入可求得a的值；当点D在点B的左侧时，连结AP，交x轴与点E.先求得AP的长，然后依据AP=12BD列出关系式，然后将m=2，a1=13a代入可求得a的值．x(斤)
0
0.75
1.00
______
2.25
3.25
y(厘米)
-2
1
2
4
7
______