


浙江省宁波市2023-2024学年第二学期八年级数学期末复习试卷解析版
展开
这是一份浙江省宁波市2023-2024学年第二学期八年级数学期末复习试卷解析版,文件包含浙江省宁波市2023-2024学年第二学期八年级数学期末复习试卷解析版docx、浙江省宁波市2023-2024学年第二学期八年级数学期末复习试卷docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
第I卷(选择题共30分)
一、选择题(本题有10小题,每小题3分,共30分.)
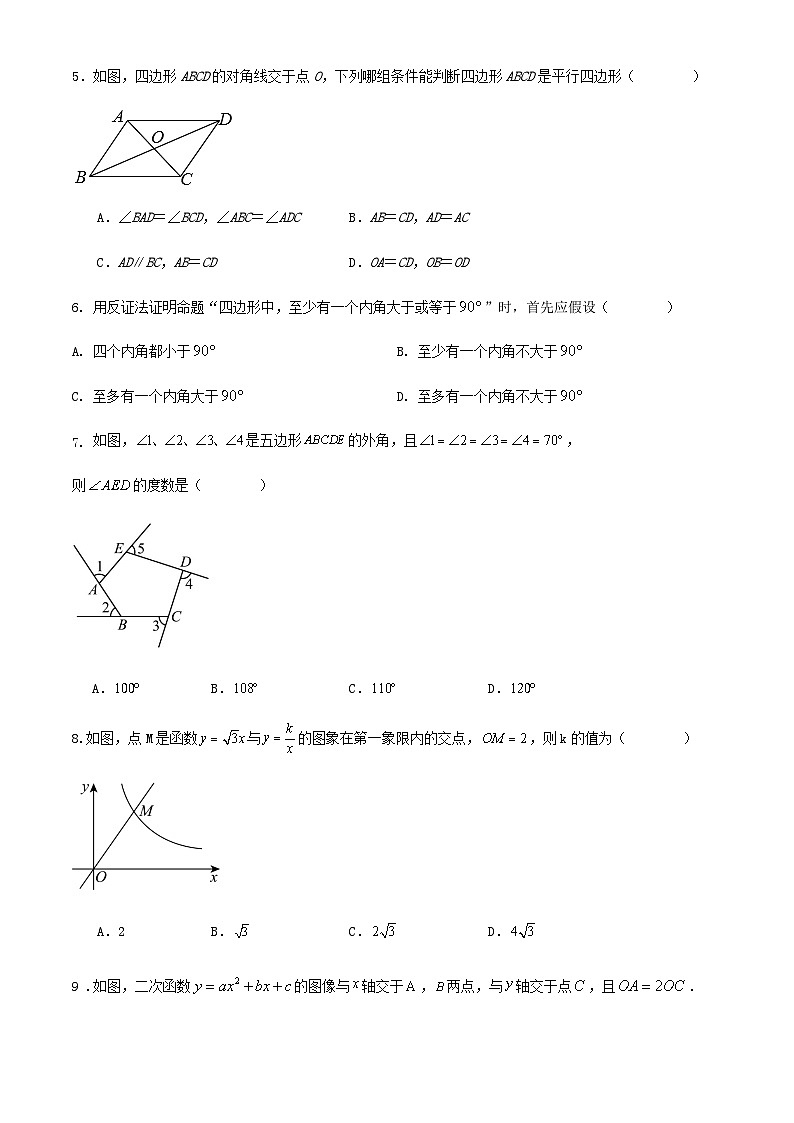
1 .下列中国品牌新能源车的车标中,是中心对称图形的是( )
A. B. C. D.
【答案】B
【分析】根据中心对称图形的定义逐项识别即可,在平面内,把一个图形绕着某个点旋转,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.
【详解】解:A.该图不是中心对称图形,故不符合题意;
B.该图是中心对称图形,故符合题意;
C.该图不是中心对称图形,故不符合题意;
D.该图不是中心对称图形,故不符合题意;
故选:B.
2. 在函数中,自变量x的取值范围是( )
A.x≥0且x≠-2B.x≥-2且x≠0C.x≥0D.x≥-2
【答案】B
【分析】由分式有意义的条件,二次根式有意义的条件进行计算,即可得到答案.
【详解】解:根据题意,
,
∴;
故选B.
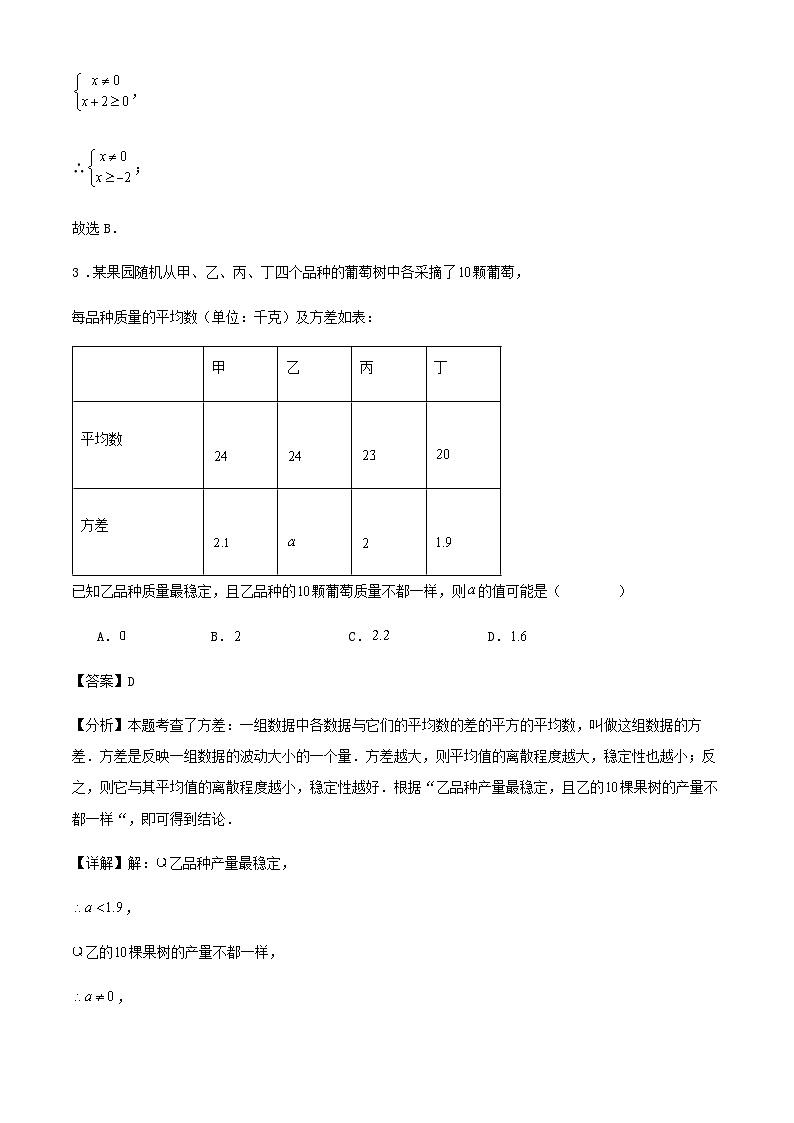
3 .某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了颗葡萄,
每品种质量的平均数(单位:千克)及方差如表:
已知乙品种质量最稳定,且乙品种的颗葡萄质量不都一样,则的值可能是( )
A.B.C.D.
【答案】D
【分析】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.根据“乙品种产量最稳定,且乙的棵果树的产量不都一样“,即可得到结论.
【详解】解:乙品种产量最稳定,
,
乙的棵果树的产量不都一样,
,
故选:.
4. 用配方法解方程,下列配方正确的是( )
A.B.C.D.
【答案】A
【分析】根据配方法求解即可.
【详解】解:
,
,
.
故选A.
5.如图,四边形ABCD的对角线交于点O,下列哪组条件能判断四边形ABCD是平行四边形( )
A.∠BAD=∠BCD,∠ABC=∠ADCB.AB=CD,AD=AC
C.AD∥BC,AB=CDD.OA=CD,OB=OD
【答案】A
【分析】根据平行四边形的判定条件逐一判断即可.
【详解】解:A、∵∠BAD=∠BCD,∠ABC=∠ADC,∠BAD+∠BCD+∠ABC+∠ADC=360°,
∴∠BAD=+∠ABC=180°,
∴,
同理可证,
∴四边形ABCD是平行四边形,故A符合题意;
B、由AB=CD,AD=AC不能判定四边形ABCD是平行四边形,故B不符合题意;
C、由AD∥BC,AB=CD不能判定四边形ABCD是平行四边形,故C不符合题意;
D、由OA=CD,OB=OD不能判定四边形ABCD是平行四边形,故D不符合题意;
故选A.
6. 用反证法证明命题“四边形中,至少有一个内角大于或等于”时,首先应假设( )
A. 四个内角都小于B. 至少有一个内角不大于
C. 至多有一个内角大于D. 至多有一个内角不大于
【答案】A
【解析】
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行解答.
【详解】解:反证法证明命题“四边形中,至少有一个内角大于或等于”时,首先应假设四个内角都小于.
故选:A.
如图,是五边形的外角,且,
则的度数是( )
A.B.C.D.
【答案】A
【分析】本题考查了多边形的外角和定理,邻补角的性质,由多边形的外角和定理可得,进而根据邻补角性质即可求出的度数,掌握多边形的外角和等于是解题的关键.
【详解】解:由多边形的外角和定理可得,,
∵,
∴,
∴,
故选:.
8.如图,点M是函数与的图象在第一象限内的交点,,则k的值为( )
A.2B.C.D.
【答案】B
【分析】作MN⊥x轴于N,设M(x,x),在Rt△OMN中,由勾股定理得出方程,解方程即可求出x,进一步即可求出k的值.
【详解】解:作MN⊥x轴于N,如图所示:
∵点M是函数与的图象在第一象限内的交点,∴设M(x,x),
在Rt△OMN中,由勾股定理得:x2+(x)2=22,解得:x=1(x=-1舍去).
∴M(1,),代入得:k=1×=;
故选:B.
9 .如图,二次函数的图像与轴交于,两点,与轴交于点,且.
则下列结论正确的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据二次函数的图像开口方向,对称轴位置,二次函数的图像与轴交点位置判断A,根据二次函数的图像与轴交点个数可得,从而判断B,由可得点坐标为,从而判断C和D.
【详解】解:∵二次函数的图像开口向下,
∴,
∵二次函数的图像的对称轴在轴右侧,
∴,
∴,
∵二次函数的图像与轴的交点在轴的上方,
∴,
∴,故A选项不符合题意;
∵二次函数的图像与轴有个交点,
∴,
∴,故B选项不符合题意;
∵二次函数的图像与轴交于,两点,与轴交于点,
∴,,
∵,
∴点坐标为,
∴,
∴,
∴,故D选项符合题意;
∵,
∴,
即,故C选项不符合题意.
故选:D.
如图,在平行四边形ABCD中,以和为斜边分别向内作等腰和等腰,
延长和分别交和于点H和F,直线分别交和于点和.
若四边形是正方形,平行四边形ABCD的面积为,
下列哪条线段的长度不能用来表示( )
A. B. C. D.
【答案】A
【解析】
【分析】设,,根据平行四边形的性质和等腰直角三角形的性质可得,根据全等三角形的判定和性质可得,根据勾股定理可得,根据正方形的性质和等腰直角三角形的性质可得,根据勾股定理可得,根据等腰直角三角形的判定和性质以及勾股定理可得,,推得,根据平行四边形的面积可得;根据面积公式逐项分析即可.
【详解】解:设,,
∵四边形是平行四边形,
∴,,
∵和都是等腰直角三角形,
∴,
又∵,
∴,
∴,
在中,,
即,
∵四边形是正方形,
∴和都是等腰直角三角形,
∴,
在中,,
∵,
∴和都是等腰直角三角形,
在中,,
∴,
∴,
∵平行四边形的面积为;
∵,
故,故选项B符合题意;
∵,,,
故,故选项C符合题意;
∵,
故,故选项D符合题意;
故选:A.
第Ⅱ卷(非选择题 共90分)
二、填空题(本题有6小题,每小题4分,共24分)
11 .已知,则化简 .
【答案】
【分析】先判断出,再根据二次根式的化简法则即可得.
【详解】解:,
,
,
故答案为:.
12. 若关于的方程有两个相等的实数根,则的值是______.
【答案】或
【解析】
【分析】根据题意可得一元二次方程根的判别式,即可得出关于的方程,解之即可求出的值.
【详解】解:∵关于的方程有两个相等的实数根,
∴,
解得:,,
∴的值是或.
故答案为:或.
13 . 小恒同学对6月1日至7日的最高气温进行统计分析制作成统计图(如图所示),
则这七天最高气温的众数是______,中位数是______.
【答案】 ①. 33 ②. 27
【解析】
【分析】结合折线统计图,根据中位数、众数的定义判断即可,众数是指出现次数最多的数据.
【详解】解:将6月1日至7日的最高气温按从小到大的顺序排列,
可得,,,,,,,
∴中位数为,
在这组数据中,33℃出现的次数最多,
∴众数为,
故答案为:33,27.
14 . 如图,在中,,分别是,的中点,,平分,交于点.
若,则的长度是______.
【答案】
【解析】
【分析】根据三角形中位线定理得到,,根据题意求出,根据平行线的性质、角平分线的定义得到,得到,进而求出.
【详解】解:∵,分别是,的中点,,
∴是中位线,
∴,,
∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
∴,
∵是的中点,
∴,
∴的长度是.
故答案为:.
如图,点是反比例函数()的图象上一点,轴,
与反比例函数的图象交于点,点,在轴上.若四边形是正方形,
则点的坐标为______.
【答案】
【解析】
【分析】设点A的坐标为,即可表示出点B的坐标为,根据正方形的性质可得,进而可得关于m的方程,解方程求出m即得答案.
【详解】解:设点A的坐标为,
∵轴,
∴点B的坐标为,
∵四边形是正方形,
∴,
∴,
解得:,负值已舍去,
∴点A的坐标为;
故答案为:.
如图,正方形的边长为6,点E,F分别在,上,,
连接、,与相交于点G,连接,取的中点H,连接,则的长为 .
【答案】
【分析】先证明,进而得,再利用勾股定理求得的值,即可求解.
【详解】解:∵四边形是正方形,
∴,,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∵点H是的中点,
∴,
∵,,
∴,
∴,
故答案为:.
解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,
第22、23题每题10分,第24题12分,共66分)
17 .解下列方程:
(1)
(2)
【答案】(1)
(2)
【分析】本题考查了配方法,因式分解法求解方程的根,选择适当解方程的方法是解题的关键.
(1)利用配方法求解即可.
(2)利用因式分解法法求解即可.
【详解】(1)解:原方程变形得:,
配方得:,
即,
直接开平方得:,
解得:.
(2)原方程变形得:,
因式分解得:,
即,
解得:.
18 .用适当的方法下列方程:
(1)
(2)
【答案】(1),;
(2),
【分析】此题考查了解一元二次方程,熟练掌握一元二次方程的解法并灵活选择是解题的关键.
(1)利用公式法解方程即可;
(2)变形后利用因式分解法解方程即可.
【详解】(1)
由题意得,,
则,
∴,
即,;
(2)
可变为,
则或
解得,;
19.“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2009年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 °,
并把条形统计图补充完整;(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑)
从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.
今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
【答案】(1)4人,6人;(2)24, 120°,见解析(3)994人
【详解】解:(1)由条形统计图可得:该校参加车模、建模比赛的人数分别是4人,6人;
(2)该校参加航模比赛的总人数:6÷25%=24,
空模所在扇形的圆心角的度数是:(24−6−6−4)÷24×360°=120°,
参加空模比赛的人数24−6−6−4=8(人),
补充条形统计图如下:
(3)32÷80=0.4,0.4×2485=994(人),
答:今年参加航模比赛的获奖人数约是994人
20. 如图,二次函数的图象经过点,.
(1)求,的值;
(2)结合图象,求当时的取值范围;
(3)平移该二次函数图象,使其顶点为点.请说出平移的方法,
并求平移后图象所对应的二次函数的表达式.
【答案】(1),
(2)
(3)先向下平移4个单位,再向左平移2个单位;
【解析】
【分析】(1)用待定系数法求解即可;
(2)由(1)得出抛物线解析式,在求出抛物线与轴的交点,结合图象求出的取值范围;
(3)先确定顶点坐标,再利用点和顶点的坐标特征确定平移的方向与距离,然后利用顶点式写出平移后的抛物线解析式.
【小问1详解】
解:把,代入得,
,
解得,
,;
【小问2详解】
解:由(1)知,抛物线解析式为,
令,则,
解得或,
当时的取值范围为;
【小问3详解】
解:,
抛物线顶点为,
,
将抛物线顶点先向左平移2单位长度,再行下平移4个单位长度得到,
平移后抛物线的解析式为.
21. 如图,在平行四边形中,,分别为边,的中点,连结,,.
(1)求证:四边形是平行四边形.
(2)若,则四边形是什么特殊四边形?请证明你的结论.
【答案】(1)证明详见解析;
(2)菱形,证明详见解析.
【分析】本题主要考查了平行四边形的性质,以及菱形的判定.
(1)根据平行四边形的性质得到,,根据平行四边形的判定定理即可得到结论;
(2)直角三角形中,是斜边上的中线,因此,进而可得出四边形是个菱形.
【详解】(1)四边形为平行四边形,
,,
、分别为边、的中点,
,,
四边形为平行四边形;
(2)若,则四边形是菱形.
证明:,
是直角三角形,且.
是的中点,
.
在▱中,,分别为边,的中点,
且,
四边形是平行四边形.
∵,
四边形是菱形.
22.2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行,冬奥会吉祥物为“冰墩墩”.
(1)据市场调研发现,某工厂今年二月份共生产500个“冰墩墩”,为增大生产量,该工厂平均每月生产量增长率相同,四月份该工厂生产了720个“冰墩墩”,求该工厂平均每月生产量增长率是多少?
(2)已知某商店“冰墩墩”平均每天可销售20个,每个盈利40元,在每个降价幅度不超过10元的情况下,每下降2元,则每天可多售10件.如果每天要盈利1440元,则每个“冰墩墩”应降价多少元?
【答案】(1)该工厂平均每月生产量的增长率为
(2)每个“冰墩墩”应降价4元
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设该工厂平均每月生产量增长率为x,利用该工厂四月份生产“冰墩墩”的数量=该工厂二月份生产“冰墩墩”的数量(该工厂平均每月生产量的增长率),即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)设每个“冰墩墩”降价y元,则每个盈利元,平均每天可售出个,利用总利润每个的销售利润日销售量,即可得出关于y的一元二次方程,解之取其符合题意的值即可得出结论.
【详解】(1)设该工厂平均每月生产量的增长率为x,
依题意得:,
解得:,(不符合题意,舍去).
答:该工厂平均每月生产量的增长率为.
(2)设每个“冰墩墩”降价y元,则每个盈利元,平均每天可售出个,
依题意得:,
整理得:,
解得:,(不符合题意,舍去).
答:每个“冰墩墩”应降价4元.
23. 如图1,两个全等的直角三角形和的斜边和在同一直线上,,将沿直线平移,并连接,.
基础巩固】
(1)求证:在沿直线平移过程中,四边形平行四边形;
【操作思考】
(2)如图2,已知,,当沿平移到某一个位置时,四边形为菱形,求此时的长;
【拓展探究】
(3)如图3,连接,若四边形为菱形,且,求的度数.
【答案】(1)证明见解析;(2);(3)
【解析】
【分析】(1)根据全等三角形的性质可得,,由平行线的判定可得,即可得证;
(2)如图2,作于,根据勾股定理可得,根据三角形的面积公式可得,可得,由勾股定理可得,根据菱形的性质得到,由等腰三角形的三线合一性质可得,最后由可得答案;
(3)延长交于点,证明,得,所以是等腰直角三角形,然后根据菱形的性质即可解决问题.
【详解】(1)证明:∵,
∴,,
∴,
∴四边形为平行四边形.
(2)解:如图2,作于,
∵,,,
∴,
∵,
∴,
∵,
∴,
∴,
在中,,
∵四边形为菱形,
∴,
∴,
∴.
(3)如图3,延长与交于点,
∵,
∴,
∴,
∵,
∴,
∴,
在菱形中,,,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∴的度数的.
24.如图,在矩形中,,,连接,点为的中点,点为边上的一个动点,连接,作,交边于点.已知点从点开始,以的速度在线段上移动,设运动时间为.解答下列问题:
(1)当为何值时,?
(2)连接,设的面积为,求与的函数关系式;
(3)在运动过程中,是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由;
(4)连接,在运动过程中,是否存在某一时刻,使恰好将分成面积比为的两部分?若存在,直接写出的值;若不存在,请说明理由.
【答案】(1)3;(2);(3)或;(4)
【分析】(1)根据平行线分线段成比例定理列式得方程,求解即可;
(2)证明△,求得,分和两种情况,结合求解即可;
(3)根据列出方程求解即可;
(4)分两种情况讨论,利用相似三角形的性质和三角形的面积公式可求解.
【详解】解:(1)∵
∴
∴
解得,
∴当时,;
(2)取AB的中点M,BC的中点N,连接OM,ON,如图①
∵
∴,,
∴∠,∠
∴四边形OMBN是矩形
∴∠
∴∠,∠
∴∠
∴△
∴
∵,
∴
①当时,,(如图①)
∴,
∴,
,
∴
=
=
∴;
②当时,如图②
此时,,,
∴
∴
∴
=
=
∴
综上所述,
(3)∵
∴
解得,
∴当或时,;
(4)当时,即,作,如图③
∵∠,∠
∴△
∴,则
∴,则
∵∠,∠
∴
∴,则
∴
∵
∴
解得,
当时,即,如图④,
同上可得,,
∵
∴
解得,
综上所述,甲
乙
丙
丁
平均数
方差
相关试卷
这是一份2023-2024学年第二学期浙江省宁波市八年级数学期末复习试题(原卷版+含解析),共38页。
这是一份2023-2024学年浙江省宁波市海曙区兴宁中学八年级(下)期中数学试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年度第二学期浙江省杭州市八年级数学期末复习训练试卷解析,文件包含2023-2024学年度第二学期浙江省杭州市八年级数学期末复习训练试卷解析doc、2023-2024学年度第二学期浙江省杭州市八年级数学期末复习训练试卷doc等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。








