

2024年黑龙江省齐齐哈尔市铁锋区中考二模数学试题
展开1.考试时间120分钟.
2.全卷共三道大题,总分120分.
一、选择题(每小题3分,共30分)
1.下列各式中,最简二次根式为( )
A.B.C.D.
2.下列图形中既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
3.不等式组的解集在数轴上表示正确的是( )
A.B.
C.D.
4.从一副扑克牌中取出两组脾,其中一组是黑桃A(算1)、2、3、4、5,另一组是方块A、2、3、4、5,将两组扑克的背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于4的概率是( )
A.B.C.D.
5.九年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多”乙说:“二班同学投中次数最多与最少的相差6个”.上面两名同学的议论能反映出的统计量是( )
A.平均数和众数B.众数和方差C.中位数和极差D.众数和极差
6.为迎接端午节,超市用一些装有同种饮料的正方体纸箱做造型,其俯视图如图所示,其中正方形中的数字表示该位置上的正方体纸箱的个数,那么该造型的左视图是( )
6题图
A.B.C.D.
7.足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是( )
A.1或2B.2或3C.3或4D.4或5
8.如图,在矩形ABCD中,AB=4,AD=3,连接BD,分别以B,D为圆心,大于的长为半径作弧,两弧交于点E,F,作直线EF分别交线段AB,BD于点G,H.连接CH,则四边形BCHG的周长为( )
8题图
A.B.11C.D.
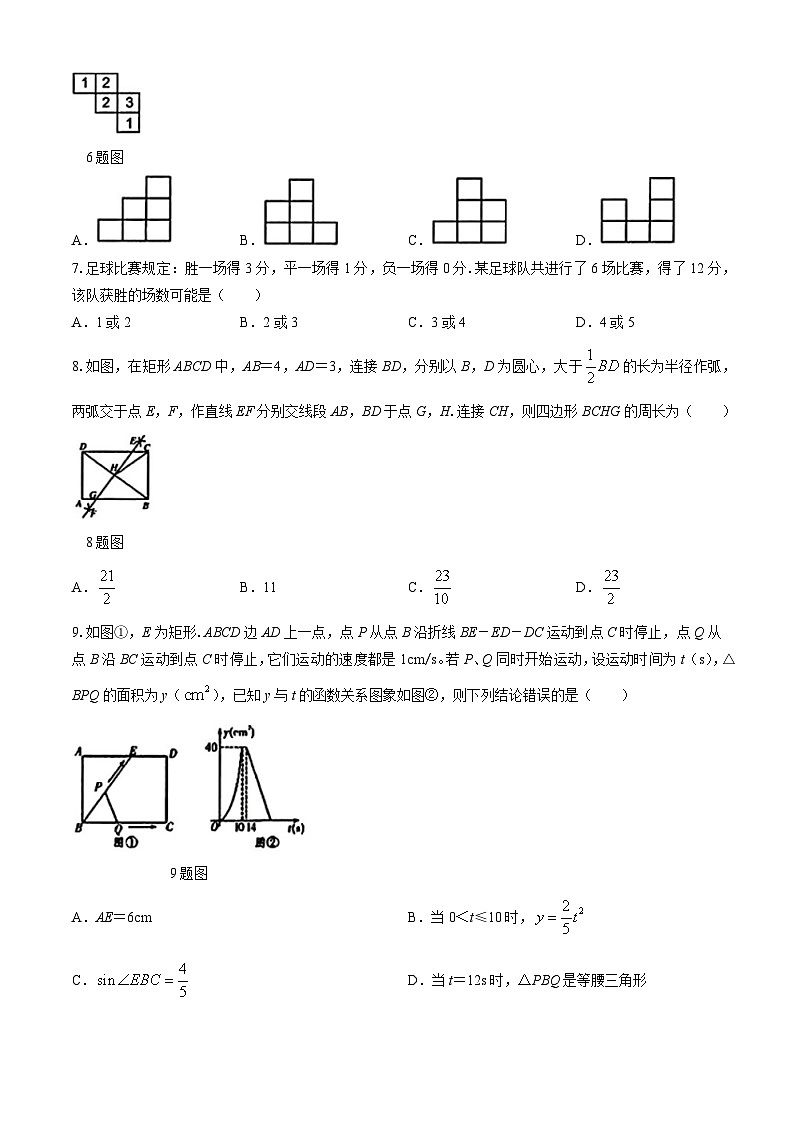
9.如图①,E为矩形.ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s。若P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(),已知y与t的函数关系图象如图②,则下列结论错误的是( )
9题图
A.AE=6cmB.当0<t≤10时,
C.D.当t=12s时,△PBQ是等腰三角形
10.如图,抛物线交x轴于,,交y轴负半轴于点C,顶点为D,下列结论:
①abc<0;②2c<3b;③若方程的两根分别为m,n,则m+n=2;④当△ABD是等腰直角三角形时,a=0.5;⑥抛物线上有两点、,且,若,则.正确的有( )
10题图
A.5B.4C.3D.2
二、填空题(每小题3分,满分21分)
11.某种病毒近似于球体,它的半径约为0.00000000495米,用科学记数法表示为 米.
12.如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,请添加一个适当的条件 ,使得△ABC≌△DEF.
12题图
13.一个圆锥的高为,侧面展开图是半圆,则圆锥的侧面积是 .
14.若关于x的分式方程有非负数解,则a的取值范围是 .
15.如图,如图,点A、B都在反比例函(k>0)的图像上,过点B作BC∥x轴交y轴于点C,连接AC并延长交x轴于点D,若DA=3DC,,则k的值为 .
15题图
16.如图,Rt△ABC中,∠C=90°,AC=3,点D在边BC上,CD=1,BD=3.点P是线段AD上一动点,当半径为1的⊙P与△ABC的一边相切时,AP的长为 .
16题图
17.在平面直角坐标系中,抛物线的图象如图所示,已知A点坐标为,过点A作轴交抛物线于点,过点作交抛物线于点,过点作轴交抛物线于点,过点作交抛物线于点……,依次进行下去,则点的坐标为 .
17题图
三、解答题(本题共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:
(2)因式分解:
19.(本题满分5分)
解方程:
20.(本题满分8分)
市教育局非常重视学生的身体健康状况,为此在5月的体育考试后对部分学生的中考体育成绩进行了调查(分数为整数,满分100分),并根据成绩(最低分为53分)分别绘制了如下统计表和统计图.(如图)
(1)本次调查的样本容量为 .
(2)请补全频数分布直方图.
(3)若此次测试成绩的中位数为78分,请直接写出:78.5~89.5分之间的人数最多有 人.
(4)若全市参加考试的学生为6300人,估计成绩优秀的学生约有多少人.(80分及80分以上为优秀)
21.(本题满分10分)
如图,AB是⊙O的直径,点C、E在⊙O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.
(1)求证:EF与⊙O相切.
(2)若BF=1,,求BC的长.
22.(本题满分10分)
一辆轿车从A市驶往B市,一小时后,一辆货车从B市驶往A市,两车沿相同路线匀速行驶,轿车到达B市停留一段时间后,按原路原速返回A市,货车到达A市比轿车返回A市早2.5h,轿车比客车每小时多行驶40km,两车到达A市后均停止行驶,两车距A市的路程S(km)与矫车行驶的时间t(h)之间的函数图像如图所示:
结合图像信息解答下列问题:
(1)A市和B市之间的路程为 km.轿车行驶的速度 km/h.轿车在B市停留了
小时.
(2)求轿车从B市返回A市时的函数解析式,并写出自变量取值范围.
(3)请直接写出轿车行驶多长时间时,与货车相距200km.
23.综合与实践(本题满分12分)
数学实践课堂上,张老师从一道基础题入手,通过不断变化题目,引导学生们发现解决此类问题的图形中的基本图形,进而通过构造基本图形,解决问题.
(1)基础题:
如图1,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,AP⊥PC。
图1
①若AP=PC,则△ABP与△PDC的关系为 .
②若,且a≠b,则 .
(2)构造应用
①如图2,点E是正方形ABCD边BC上一点,∠AEF=90°,AE=EF,AF与CD交于点G,连接CF,请直接写出∠GCF= °.
图2
②如图3,沿△ABP的边AB、AC向外作矩形ABDE和矩形ACFG,,连接EG,AH是BC边上的高,延长HA交EG于点K,求证:K是EG中点,并直接写出BC与AK的数量关系:BC= AK.
图3
(3)综合应用
如图4,在矩形ABCD中,AB=4,BC=6,点E是边AD上的动点(点E不与点A、D重合),连接CE,过点E作EF⊥CE,交AB于点F,连接CF,过点B作BG⊥CF,垂足为G,点M是BC边的中点。请直接写出当AG+GM值最小时DE的值为: .
图4
24.综合与实践(本题满分14分)
已知抛物线与x轴交于A、两点,与y轴交于点,点P为第一象限抛物线上的动点.
(1)求抛物线的解析式及对称轴.
(2)如图1,
图1
①若∠PCB=∠ACO,则P点坐标为 ;
②若∠PCB=2∠ACO,则P点坐标为 .
(3)如图2,连接AP、BC,AP与BC交于点D,若PD∶AD=3∶5,求点P坐标.
图2
(4)如图3,M、N是抛物线对称轴上两个动点,点H在点N上方,且MN=2,请直接写出CM+CN的最小值 .并写出此时M点的坐标 .
图3
初三质量监测数学参考答案及评分标准
2024.5
一、选择题(每题3分、共30分)
二、填空题(每题3分、共21分)
三、解答题(共69分)
18.计算(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)解:
(2)解:原式
19.解方程(本题满分5分)
,.
20.(本题满分8分)
(1)45.
(2)画图略画出条形图和在纵轴标注数字“12”
(3)14
(4)(人)
答:基于本次调查,估计成绩优秀的学生约有2800人。(没有“估计”或“约有”字样不得分)
21.解
(1)证明:连接OE
∵弧BE=弧BE,
∴∠EOB=2∠EAB,
∵∠CAB=2∠EAB,
∴∠CAB=∠EOB,
∵AB是⊙O的直径
∴∠C=90°,
∵∠AFE=∠ABC,
∴△OFE∽△ABC,
∴∠OEF=∠C=90°
∴OE⊥EF
∵OE为⊙O半径
∴EF是⊙O的切线.
(2)设⊙O的半径为r.则OE=r,OF=r+1
∵∠OEF=90°
∴即
∴r=4
∴AB=8
∵∠AFE=∠ABC
∴
∴
∴
∴
22.(本题满分10分)
解:
(1)720,120,0.5
(2)设轿车从B市返回A市时的函数解析式为S=kt+b(k≠0),
轿车速度120km/h
轿车从B市返回A市所需时间为:720÷120=6(h)
货车速度为:120-40=80(km/h)
货车全程所需时间为:720÷80=9(h)
∴轿车往返共用时间为:9+1+2.5=12.5(h)
∴,,
∴
解得
∴轿车从B市返回A市时的函数解析式为S=-120t+1500(6.5≤t≤12.5)
(3)3h或5h或h
23.综合与实践(本题满分12分)
解:
(1)①△ABP≌△PDC
②
(2)①45
②证明:过点E作EQ⊥AK于Q,过点G作GR⊥AK交AK的延长线于R.
∵四边形ABDE是矩形
∴∠BAE=90°
∴∠BAH+∠QAE=180°-∠BAE=90°
∵∠AQE=90°
∴∠QAE+∠QEA=90°
∴∠BAH=∠QEA
∵∠BHA=∠AQE=90°
∴△BHA∽△AQE
∴AH∶QE=AB∶AE
同理:△CHA∽△ARG
∴AH∶RG=AC∶AG
∵AB∶AE=AC∶AG
∴AH∶QE=AH∶RG
∴QE=RG
∵∠EQK=∠GRK=90°
∴∠QEK=∠RGK
∵∠EKQ=∠GKR
∴△EKQP≌△GKR(AAS)
∴EK=KG,即K是EG中点.
(3)或
24.综合与探究(本题满分14分)
(1)
对称轴为
(2)①,②
(3)过点A作AH⊥x轴与BC的延长线交于点H,过点P作PF⊥x轴与BC交于点E
当y=0时x=-1或x=4,
∴
∴OA=1,AB=5
∵∠HAB=∠PFB=90°
∴PF∥AH
∴△PDE∽△ADH
∴PE∶AH=PD∶AD=3∶5
∵Rt△COB中,
∴Rt△HAB中,
∴AH=2.5
∴
∴
∵,
∴直线BC的解析式为
设()
则
∴
解得:,
∴或
(4),
说明:本套试卷中所有题目,若由其它方法得出正确结论,都可参照本评分标准酌情给分.
题号
一
二
三
总分
18
19
20
21
22
23
24
得分
分数
59.5分以下
69.5分以上
69.5分以上
79.5以上
89.5以上
人数
3
42
32
20
8
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
B
A
D
B
C
A
D
C
题号
11
12
13
14
15
16
17
答案
AB=DE或∠A=∠D或∠ACB=∠DFE
且
4
或或
2021年黑龙江省齐齐哈尔市铁锋区九年级中考模拟数学试题: 这是一份2021年黑龙江省齐齐哈尔市铁锋区九年级中考模拟数学试题,共14页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
2023年黑龙江省齐齐哈尔市铁锋区中考数学二模试卷(含解析): 这是一份2023年黑龙江省齐齐哈尔市铁锋区中考数学二模试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年黑龙江省齐齐哈尔市铁锋区中考三模数学试题: 这是一份2023年黑龙江省齐齐哈尔市铁锋区中考三模数学试题,共7页。












