04，山东省淄博市临淄区2023-2024学年八年级下学期期中数学试题

这是一份04，山东省淄博市临淄区2023-2024学年八年级下学期期中数学试题，共9页。试卷主要包含了选择题，填空题，解答题解答要写出必要的文字说明等内容，欢迎下载使用。

本试卷共8页，满分150分，考试时间120分钟．考试结束后，将本试卷和答题卡一并交回。
一、选择题（本题共10小题，在每小题所给出的四个选项中，只有一个是正确的，每小题4分，满分40分，错选、不选、多选，均记0分．）
1．下列各式中不是二次根式的是（ ）
A．B．C．D．
2．下列方程一定是一元二次方程的是（ ）
A．B．C．D．
3．一元二次方程的二次项系数、一次项系数、常数项分别是（ ）
A．3，1，B．3，2，1C．3，，D．3，2，
4．若和最简二次根式是同类二次根式，则的值为（ ）
A．B．C．D．
5．把方程化成的形式，则的值是（ ）
A．17B．15C．9D．7
6．根据表格中的信息，估计一元二次方程（，，为常数，）的一个解的范围为
A．B．C．D．
7．关于的一元二次方程有一个根为0，则的值为（ ）
A．1B．C．D．不确定
8．以为根的一元二次方程可能是（ ）
A．B．C．D．
9．把根号外的因式移入根号内，其结果为（ ）
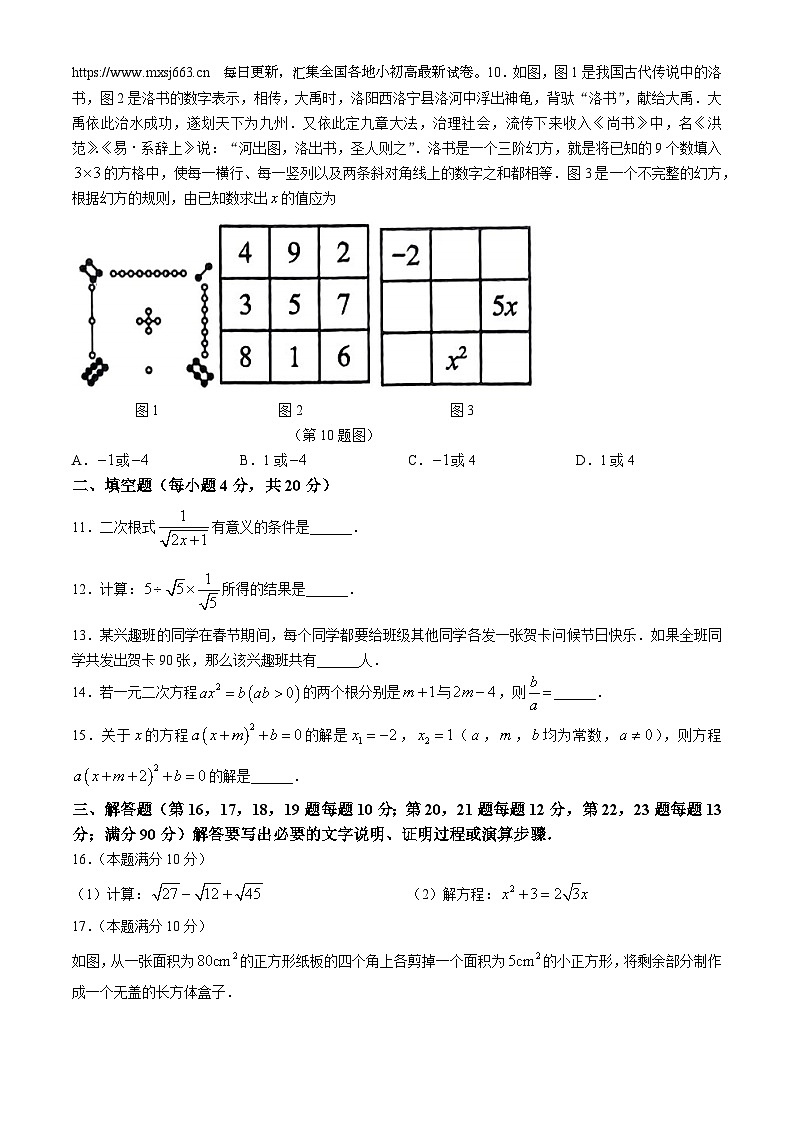
A．B．C．D．试卷源自 每日更新，汇集全国各地小初高最新试卷。10．如图，图1是我国古代传说中的洛书，图2是洛书的数字表示，相传，大禹时，洛阳西洛宁县洛河中浮出神龟，背驮“洛书”，献给大禹．大禹依此治水成功，遂划天下为九州．又依此定九章大法，治理社会，流传下来收入《尚书》中，名《洪范》．《易・系辞上》说：“河出图，洛出书，圣人则之”．洛书是一个三阶幻方，就是将已知的9个数填入的方格中，使每一横行、每一竖列以及两条斜对角线上的数字之和都相等．图3是一个不完整的幻方，根据幻方的规则，由已知数求出的值应为
图1 图2 图3
（第10题图）
A．或B．1或C．或4D．1或4
二、填空题（每小题4分，共20分）
11．二次根式有意义的条件是______．
12．计算：所得的结果是______．
13．某兴趣班的同学在春节期间，每个同学都要给班级其他同学各发一张贺卡问候节日快乐．如果全班同学共发出贺卡90张，那么该兴趣班共有______人．
14．若一元二次方程的两个根分别是与，则______．
15．关于的方程的解是，（，，均为常数，），则方程的解是______．
三、解答题（第16，17，18，19题每题10分；第20，21题每题12分，第22，23题每题13分；满分90分）解答要写出必要的文字说明、证明过程或演算步骤．
16．（本题满分10分）
（1）计算：（2）解方程：
17．（本题满分10分）
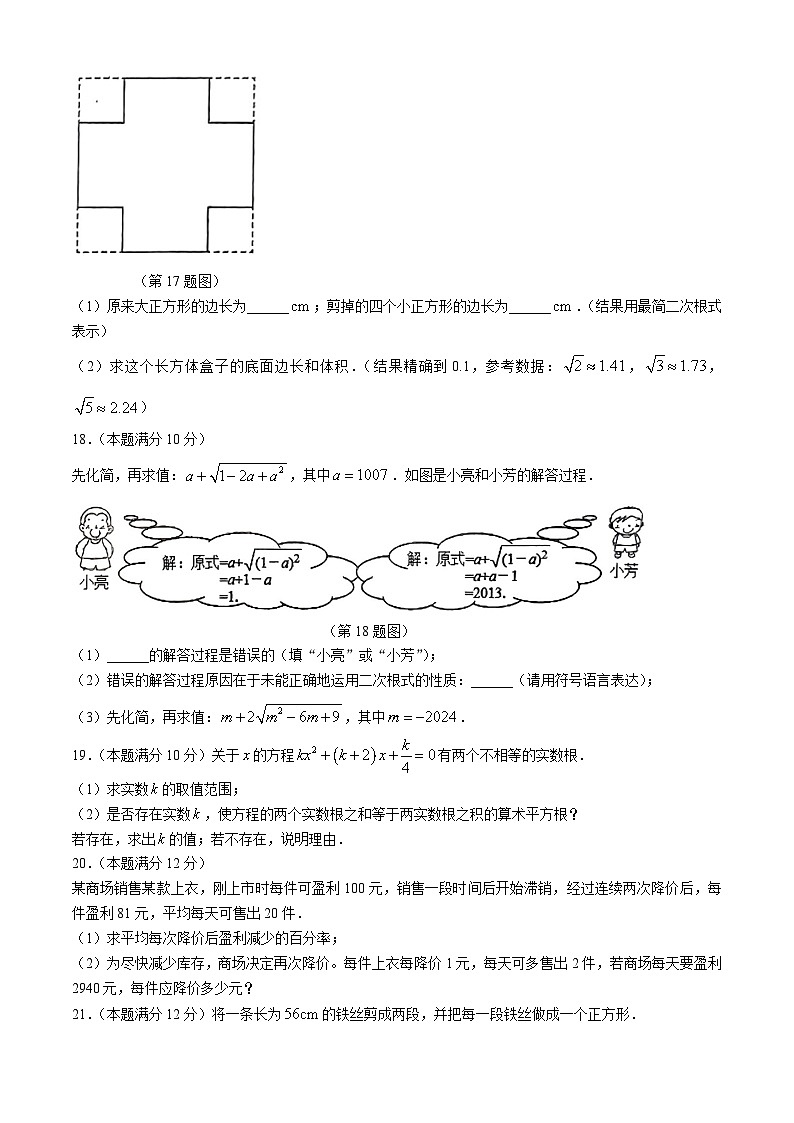
如图，从一张面积为的正方形纸板的四个角上各剪掉一个面积为的小正方形，将剩余部分制作成一个无盖的长方体盒子．
（第17题图）
（1）原来大正方形的边长为______；剪掉的四个小正方形的边长为______．（结果用最简二次根式表示）
（2）求这个长方体盒子的底面边长和体积．（结果精确到0.1，参考数据：，，）
18．（本题满分10分）
先化简，再求值：，其中．如图是小亮和小芳的解答过程．
（第18题图）
（1）______的解答过程是错误的（填“小亮”或“小芳”）；
（2）错误的解答过程原因在于未能正确地运用二次根式的性质：______（请用符号语言表达）；
（3）先化简，再求值：，其中．
19．（本题满分10分）关于的方程有两个不相等的实数根．
（1）求实数的取值范围；
（2）是否存在实数，使方程的两个实数根之和等于两实数根之积的算术平方根？
若存在，求出的值；若不存在，说明理由．
20．（本题满分12分）
某商场销售某款上衣，刚上市时每件可盈利100元，销售一段时间后开始滞销，经过连续两次降价后，每件盈利81元，平均每天可售出20件．
（1）求平均每次降价后盈利减少的百分率；
（2）为尽快减少库存，商场决定再次降价。每件上衣每降价1元，每天可多售出2件，若商场每天要盈利2940元，每件应降价多少元？
21．（本题满分12分）将一条长为的铁丝剪成两段，并把每一段铁丝做成一个正方形．
（1）要使这两个正方形的面积之和等于，该怎么剪？请说明理由；
（2）这两个正方形的面积之和可能等于吗？请说明理由．
22．（本题满分13分）
如图，一次函数的图象交轴于点，交轴于点，点在线段上（不与点，重合）过点分别作和的垂线，垂足为点，．
（第22题图）
（1）求点的坐标和线段的长度；
（2）若矩形的面积为1，求点的坐标；
（3）是否存在一点，使矩形的面积为？说明你的理由．
23．（本题满分13分）阅读材料，请回答下列问题
材料一：我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积．用现代式子表示即为：
（其中，，为三角形的三边长，为面积）而另一个文明古国古希腊也有求三角形面积的“海伦公式”：（其中）
材料二：对于平方差公式：
公式逆用可得：，
例：
（1）若已知三角形的三边长分别为3，4，5，请分别运用公式①和公式②，计算该三角形的面积；
（2）请由公式①推导公式②，并写出推导过程．
2023－2024学年度第二学期期中质量检测
初三数学试题参考答案
友情提示：解题方法只要正确，可参照得分．
一、选择题（本题共10小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项填在下面的表中．每小题4分，满分40分，错选、不选、多选，均记0分．）
二、填空题（每小题4分，共20分）
11．；12．1；13．10；
14．4；15．，
三、解答题（第16，17，18，19题每题10分；第20，21题每题12分，第22，23题每题13分；满分90分）解答要写出必要的文字说明、证明过程或演算步骤．
16．（本题满分10分）
解：（1）原式
；
（2）整理得： ，，．
， ．
17．（本题满分10分）解：（1），；
（2）这个长方体盒子的底面边长为，
这个长方体盒子的体积为．
答：这个长方体盒子的底面边长为，体积为．
18．（本题满分10分）解：（1）小亮的解答过程是错误的；
（2）二次根式的性质：（或），
（3）原式，，，
原式 ．
19．（本题满分10分）
解：（1）依题意得，，
又，的取值范围是且；
（2）不存在符合条件的实数，使方程的两个实数根之和等于两实数根之积的算术平方根，
理由：设方程的两根分别为，，
由根与系数的关系有：，
又因为方程的两个实数根之和等于两实数根之积的算术平方根，
，，
由（1）知，且，不符合题意，
不存在符合条件的实数，使方程的两个实数根之和等于两实数根之积的算术平方根．
20．（本题满分12分）
解：（1）设平均每次降价后盈利减少的百分率为，依题意，得，
解得：，（不合题意，舍去）．
答：平均每次降价后盈利减少的百分率为．
（2）设每件应降价元，则每天可售出件，
依题意，得，
解得：，
要尽快减少库存，．
答：每件应降价60元．
21．（本题满分12分）
解：设两段长度分别为，，其中，则两个正方形的面积之和
．
（1）当，即时，解得，，
当时，，；
当时，，，
剪成的一段为，另一段为；
（2）当，即时，
解得，，
，得，，均不符合题意，舍去，
这两个正方形的面积之和不可能等于．
解法2：设两段长度分别为，，其中，则两个正方形的面积之和
（1）当，即时，解得，，
剪成的一段为，另一段为；
（2）当，即时，
解得，，
，，，均不符合题意，舍去，
这两个正方形的面积之和不可能等于．
22．（本题满分13分）
解：（1）一次函数的图象交轴于点，交轴于点，
令，即 解得
令，即
（2）点在线段上（不与点，重合）
设的坐标为，
整理得 解得，
当时，，即
当时，，即 或
（3）不存在，理由如下，
依题意，设的坐标为，
整理得
，，
即原方程无实数根，则不存在点，使矩形的面积为．
（第22题图）
23．（本题满分13分）
解：（1）不妨设，，，
，，
；
，，，，
．
三角形的面积为6．
（2）
．0
0.5
1
1.5
2
5.25
13
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
C
B
C
D
A
D
B
A