
07,山东省临沂市罗庄区2023-2024学年八年级下学期期中数学试题(无答案)
展开(时间:120分钟 总分120分)
注意事项:1.答题前,请先认真浏览试卷;然后按要求操作;
2.答题时,端正心态,认真审题,认真书写,规范作图,保持卷面整洁!
一、选择题(本大题共10小题,每小题3分,共30分)
1.计算:______
A.B.C.8D.-8
2.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为B.三内角之比为
C.三边长分别为5,12,13D.三边长分别为1,,
3.估算的结果在( )
A.2和3之间B.3和4之间C.4和5之间D.5和6之间
4.实数a和b在数轴上如图所示,化简的结果是( )
A.B.C.D.
5.菱形的两条对角线长分别为6cm和8cm,则它的高为( )
A.9.6cmB.4.8cmC.1.2cmD.2.4cm
6.如图,在矩形ABCD中,,,点E在CD上,点F在BC上,将沿AF翻折,使点B的对应点恰为点E,则BF的长为( )
A.B.C.D.
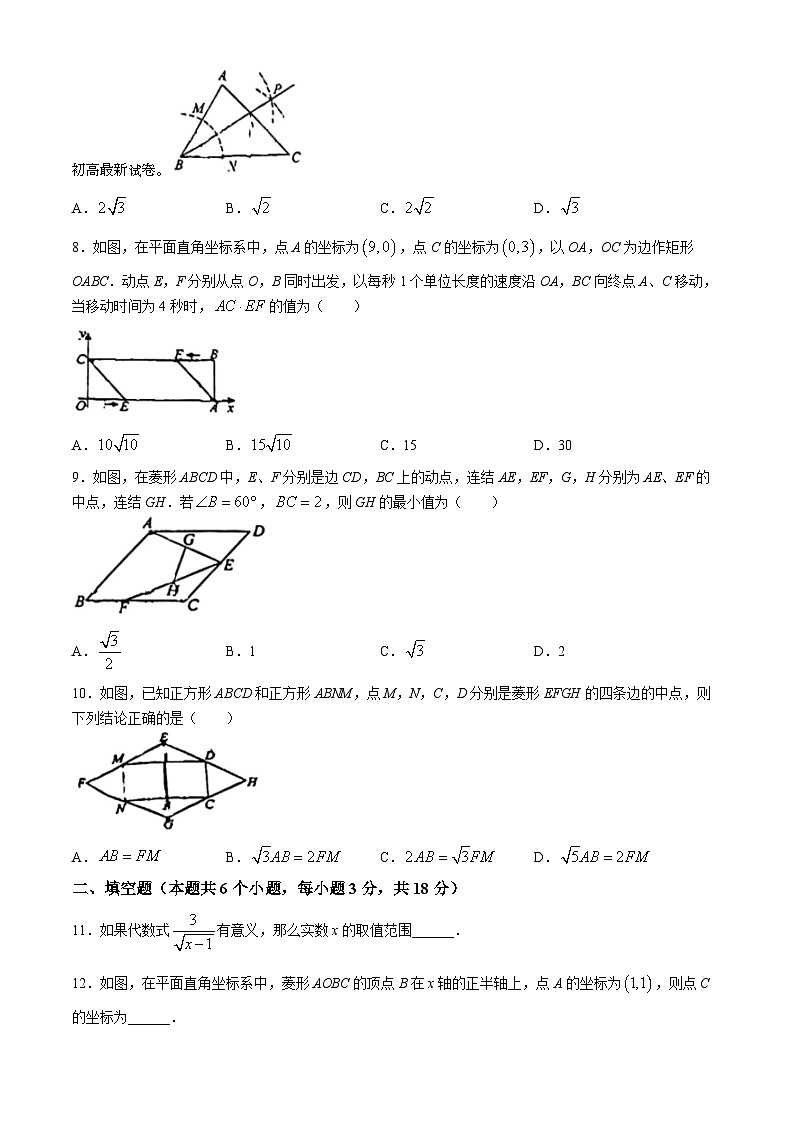
7.如图,在中,,,以点B为圆心,任意长为半径画弧,分别交BA、BC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结BP交AC于点D.若,则CD的长为( )试卷源自 每日更新,汇集全国各地小初高最新试卷。
A.B.C.D.
8.如图,在平面直角坐标系中,点A的坐标为,点C的坐标为,以OA,OC为边作矩形OABC.动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A、C移动,当移动时间为4秒时,的值为( )
A.B.C.15D.30
9.如图,在菱形ABCD中,E、F分别是边CD,BC上的动点,连结AE,EF,G,H分别为AE、EF的中点,连结GH.若,,则GH的最小值为( )
A.B.1C.D.2
10.如图,已知正方形ABCD和正方形ABNM,点M,N,C,D分别是菱形EFGH的四条边的中点,则下列结论正确的是( )
A.B.C.D.
二、填空题(本题共6个小题,每小题3分,共18分)
11.如果代数式有意义,那么实数x的取值范围______.
12.如图,在平面直角坐标系中,菱形AOBC的顶点B在x轴的正半轴上,点A的坐标为,则点C的坐标为______.
13.如图,在2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则AB边上的高为______.
14.如图,四边形ABCD是边长为2的正方形,是等边三角形,则阴影部分的面积为______.
15.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,,F为DE的中点,若的周长为18,则OF的长为______.
16.矩形ABCD的对角线AC,BD相交于点O,点F在矩形ABCD边上,连接OF,若,,则______.
三、解答题(本大题共7小题,共72分)
17.计算(本题满分10分)
(1);(2).
18.(本题满分10分)
如图,已知四边形ABCD是平行四边形,其对角线相交于点O,,,.
(1)是直角三角形吗?请说明理由;
(2)求证:四边形ABCD是菱形.
19.(本题满分9分)
如图,在中,,延长CB至D,使得,过点A,D分别作,,AE与DE相交于点E.下面是两位同学的对话:
请你选择一位同学的说法,并进行证明.
20.(本题满分11分)
图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作,点C在格点上.
(1)在图①中,的面积为;
(2)在图②中,的面积为5;
(3)在图③中,是面积为的钝角三角形.
21.(本题满分8分)
如图,已知矩形ABCD,点E在CB延长线上,点F在BC延长线上,过点F作交ED的延长线于点H,连结AF交EH于点G,.求证:.
22.(本题满分12分)
如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),,,E,F分别为垂足,连接EF,AG,并延长AG交EF于点H.
(1)求证:;
(2)判断AH与EF的位置关系,并说明理由.
23.(本题满分12分)
阅读与思考:下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.
瓦里尼翁平行四边形
我们知道,如图1,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,顺次连接E,F,G,H,得到的四边形EFGH是平行四边形.
这个平行四边形EFGH被称为瓦里尼翁平行四边形.瓦里尼翁是法国数学家、力学家.瓦里尼翁平行四边形的面积等于原四边形面积的一半.
证明:如图2,连接AC,分别交EH,FG于点P,Q,过点D作于点M,交HG于点N.
∵H,G分别为AD,CD的中点,∴,.(依据1)
易知.∵四边形EFGH是瓦里尼翁平行四边形,∴,即.
∵,即,
∴四边形HPQG是平行四边形.(依据2)
∴.∵,
∴,同理,…
任务:(1)材料中的依据1是指:______,依据2是指:______,并补全证明.
(2)请用刻度尺、三角板等工具,画一个四边形ABCD及它的瓦里尼翁平行四边形EFGH,使得四边形EFGH为矩形;(要求同时画出四边形ABCD的对角线)
(3)在图1中,分别连接AC,BD,请猜想瓦里尼翁平行四边形EFGH的周长与对角线AC、BD长度的关系,并证明你的结论.小星:由题目的已知条件,若连接CE,则可证明.
小红:由题目的已知条件,若连接BE,则可证明.
04, 山东省临沂市罗庄区2023-2024学年八年级下学期期中考试数学试题: 这是一份04, 山东省临沂市罗庄区2023-2024学年八年级下学期期中考试数学试题,共4页。
03, 山东省临沂市罗庄区2023-2024学年九年级下学期期中考试数学试题: 这是一份03, 山东省临沂市罗庄区2023-2024学年九年级下学期期中考试数学试题,共4页。试卷主要包含了6米.已知目高为1,1m,参考值,75等内容,欢迎下载使用。
山东省临沂市罗庄区2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份山东省临沂市罗庄区2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含山东省临沂市罗庄区2023-2024学年八年级下学期期中数学试题原卷版docx、山东省临沂市罗庄区2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。












