

26,河南省洛阳市涧西区2023—-2024学年八年级下学期期中考试数学试卷
展开
这是一份26,河南省洛阳市涧西区2023—-2024学年八年级下学期期中考试数学试卷,共10页。试卷主要包含了试题卷上不要答题,请用0,矩形具有而菱形不具有的性质是,如图,在▱ABCD中,等内容,欢迎下载使用。
注意事项:
1.本试卷分试题卷和答题卡两部分,试题卷共4页,满分120分,考试时间100分钟。
2.试题卷上不要答题,请用0.5毫米黑色签字水笔直接把答案写在答题卡上,答在试题卷上的答案无效。
3.答题前,考生务必将本人姓名、准考证号填写在答题卡第一面的指定位置上。
一、选择题(每小题3分,共30分)
1.下列二次根式中,是最简二次根式的是( )
下列式子化简后能与 3合并的是( )
下列运算正确的是( )
A.2+3=5B.23-3=1C.3×23=33D.8÷2=24.已知△ABC的三边分别为a,b,c,下列条件不能判定△ABC为直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=∠B+∠C
C.b²=a²-c² D.a²:b²:c²=1:2:35.矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线互相垂直
C.对角线相等 D.两组对角分别相等
6.如图,四边形ABCD的对角线交于点O,下列能判断四边形ABCD是平行四边形的是( )
A. OA=OC,AB=CD
B. AB∥CD,∠BAC=∠ACD
C.∠BAD=∠BCD,AB∥CD
D. AB=CD,AD∥BC
7.如图,在菱形ABCD中,对角线AC、BD交于点F,E是AB的中点,若EF=1,则菱形ABCD的周长是( );
A.8 B.6
C.4 D.2
8.如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中 试卷源自 每日更新,汇集全国各地小初高最新试卷。AE=5,AB=13,,则EF的值是( )
A.23
B.13 C.7
D.729.如图,在矩形OABC中,点B的坐标是( -24,则AC的长是 .
A.2
B.23C.4
D.2510.如图,在▱ABCD中,. ∠C=120°,AB=8,点H,G分别是边DC,BC上的动点,连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为( )
A.3 B.32 C.23 D.4
二、填空题(每小题3分,共15分)
11.若 x-2有意义,则实数x应满足的条件为 .
12.如果一个无理数a与. 12的积是一个有理数,写出a的一个值是 。
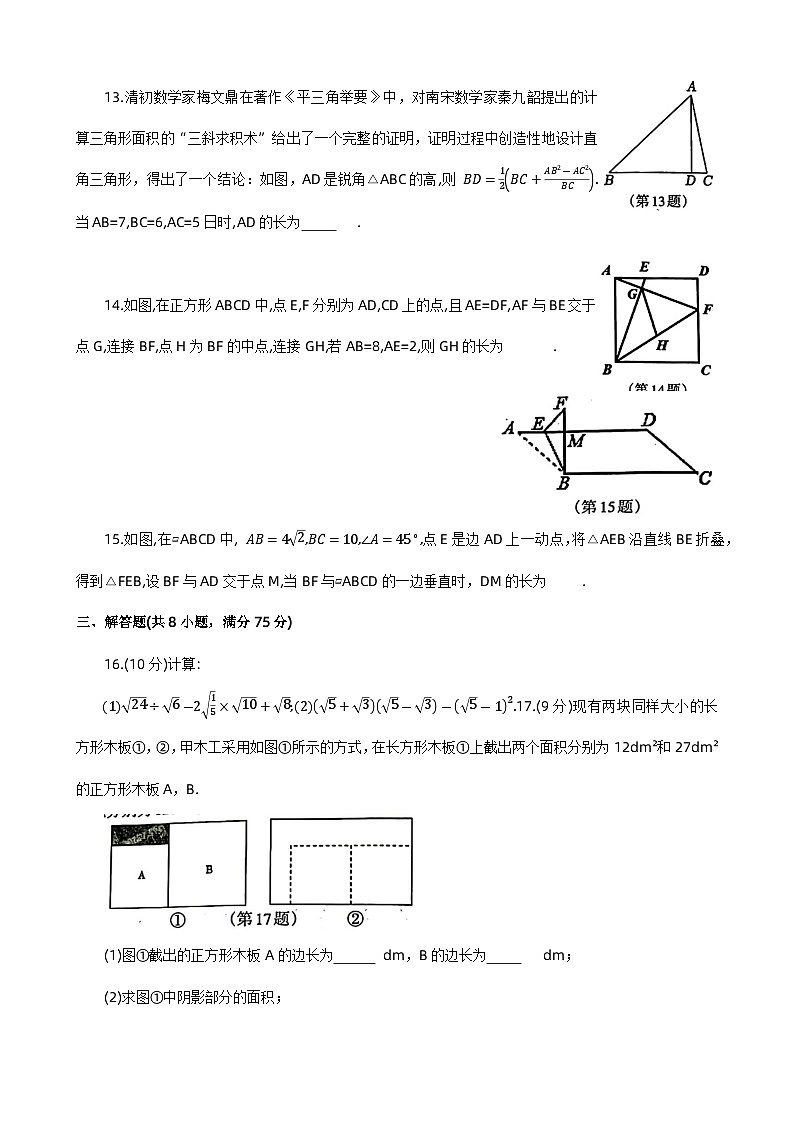
13.清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论:如图,AD是锐角△ABC的高,则 BD=12BC+AB2-AC2BC.当AB=7,BC=6,AC=5日时,AD的长为 .
14.如图,在正方形ABCD中,点E,F分别为AD,CD上的点,且AE=DF,AF与BE交于点G,连接BF,点H为BF的中点,连接GH,若AB=8,AE=2,则GH的长为 .
15.如图,在▱ABCD中, AB=42,BC=10,∠A=45∘,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与▱ABCD的一边垂直时,DM的长为 .
三、解答题(共8小题,满分75分)
16.(10分)计算:
124÷6-215×10+8;25+35-3-5-12.17.(9分)现有两块同样大小的长方形木板①,②,甲木工采用如图①所示的方式,在长方形木板①上截出两个面积分别为12dm²和27dm²的正方形木板A,B.
(1)图①截出的正方形木板A的边长为 dm,B的边长为 dm;
(2)求图①中阴影部分的面积;
(3)乙木工想采用如图②所示的方式,在长方形木板②上截出面积为 25dm²的两个正方形木板,请你判断能否截出,并说明理由.
18.(9分)如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,点O是AC的中点.请你添加一个条件(不另加辅助线)使四边形ABCD成为矩形.
(1)添加的条件是 ;
(2)请给出证明过程.
_____________________________________________
19.(9分)如图,BD是▱ABCD的对角线,BM平分∠DBC,交CD于点M.
(1)请用无刻度的直尺和圆规作∠ADB的角平分线DN,交AB于点N(要求:保留作图痕迹,不写作法);
(2)求证:四边形BMDN为平行四边形.
20.(9分)如图,4×4正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B都在格点上,按下列要求作图,使得所画图形的顶点均在格点上.
(1)在图①中画一个Rt△ABC,使 ∠A=45∘,AC=5;
(2)在图②中画▱ABCD,使其面积为6.
21.(9分)消防云梯的作用主要是用于高层建筑火灾等救援任务,消防云梯的使用可以大幅提高消防救援的效率,缩短救援时间,减少救援难度和风险.如图,已知云梯最多只能伸长到25m(即AB=CD=25m),消防车车身高3.5m(即点A到地面EF的距离AH为3.5m),救人时云梯伸长至最长,在完成从18.5m(即BE=18.5m)高的B处救人后,还要到点B的正上方5m(即BD=5m)高的D处救人,这时消防车需要从A处向着火的楼房靠近的水平距离AC为多少米?(提示:延长AC交DE于点O,则AO⊥DE).
22.(10分)如图,在正方形ABCD中,对角线AC所在的直线上有两点M,N满足AN=CM,连接BM,BN,DM,DN.
(1)试判断四边形BMDN的形状,并说明理由.
(2)若 AD=2,∠DNM=30∘,求四边形BMDN的面积.
23.(10分)定义:如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形ABCD沿对角线AC对折后完全重合,四边形ABCD是以直线AC为对称轴的“忧乐四边形”.
(1)下列四边形一定是“忧乐四边形”的有 (填序号);
①平行四边形②菱形③矩形④正方形
(2)如图2,在矩形ABCD中,点E是BC边上的中点,四边形ABEM是以直线AE为对称轴的“忧乐四边形”(点M在四边形ABCD内部),连接AM并延长交DC于点N.
求证:四边形MECN是“忧乐四边形”.
(3)如图3,在四边形ABCD中,AB∥CD,AD∥BC,AB=3,AD=5,点E是BC边上的中点,四边形ABEM是以直线AE为对称轴的“忧乐四边形”(点M在四边形ABCD内部),连接AM并延长交DC于点N.当△ADN是直角三角形时,请直接写出线段CN的长.
八年级期中试卷答案
1-5 BBDAC 6-10 CADDC
11、 x≥2
12、 3
13、 2 6
14、5
15、2或6
三、解答题
16. (1) 原式 =2-22+22 ……3分
=2: ……5分
(2) 原式 =5-3-5-25+1 ……9分
=2-6+25 =25-4. ……10分
17.123,33; ……2分
(2)根据题意得:长方形的长为 23+33=53dm,宽为 33dm,
∴阴影部分的面积: =33-23×23=6dm2. …6 分
(3)不能截出,理由如下:
∵面积为25dm²|的两个正方形木板的边长均为 25=5dm,
5+5=10=100>75=53,∴不能在长方形木板②上截出面积为 25dm²的两个正方形木板. ……9分
18. (1) AC=BD (答案不唯一); ……2 分
(2) 证明: ∵AB∥CD,
∴∠ABO=∠CDO,
∵O是AC的中点,
∴OA=OC,
∵∠AOB=∠COD,
∴△AOB≌△COD (AAS), ……5分
∴OD=OB,
∵OA=OC,
∴四边形ABCD 是平行四边形, ……7分
又∵AC=BD,
∴□ABCD是矩形. ……9分19. (1) 作图如下:
DN即为所求; ……3分
(2) 证明: ∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠ADB=∠DBC. ……5分
又∵DN平分∠ADB, BM平分∠DBC,
∴∠NDB=12∠ADB,∠DBM=12∠DBC.∴∠NDB=∠DBM.
∴DN∥BM, …7分
又∵四边形ABCD是平行四边形.
∴BN∥DM.
∴四边形DNBM为平行四边形. ……9分
20.
(答案不唯一); ……5分
(答案不唯一); ……9分
21. 解: ∵∠AOE=∠E=∠AHE=90°
∴四边形AOEH是矩形
∴OE=AH=3.5, AO=EH ……2分
在Rt△ABO中,
∵AB=25m, OB=18.5-3.5=15(m),
∴AO=AB2-OB2=252-152=20m,在Rt△COD中, ……5 分
∵∠COD=90°, CD=25m, OD=OB+BD=20(m),
∴OC=CD2-OD2=252-202=15m∴AC=OA-OC=5 (m),
答: AC为5m. ……9分
22. (1) 解: 四边形 BMDN是菱形, ………1 分
理由如下: 连接BD, 交AC 于O,
∵四边形 ABCD 是正方形,
∴OA=OC, OD=OB, AC⊥BD, ……2分
∵AN=CM,
∴ON=OM,
∴四边形BMDN是平行四边形, ……4分
∵AC⊥MN,
∴四边形BMDN 是菱形. …………5分
(2) 在Rt△AOD 中, AO²+OD²=AD²,
∵AO=OD, AD= 2,
∴OD=1,
∴BD=2OD=2 ……7分
在 Rt△AOD中, ∠DNM=30°,
∴DN=2OD=2,
∴ON=DN2-OD2=22-12=3 ∴MN=2ON=23 ……9分
∴S菱形BMDN=12BD∘MN=23 …10分
23. (1) ②④; ……2分
(2) 证明: 如图2, 连接EN, ∵四边形ABCD 是矩形,
∴∠B=∠C=90°,
∵E是BC的中点,
∴EB=EC,∵将 △ABE沿AE折叠后得到 △AME,
∴∠AME=∠B=90°,EM=EB, ……4分
∴∠EMN=180°-∠AME=90°=∠C,∴EM=EC,∵EN=EN, ∴Rt△EMN≅Rt△ECNHL, ………7 分
∴四边形MECN沿 EN折叠完全重合 ,
∴四边形MECN是“忧乐四边形”; ……8分
3142或 2512. ………10分
相关试卷
这是一份河南省洛阳市涧西区2022-2023学年八年级下学期期中数学试卷(含答案),共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年河南省洛阳市涧西区洛阳市数学九上期末联考模拟试题含答案,共8页。试卷主要包含了下列说法正确的是,二次函数图象如图所示,下列结论,如图,是用棋子摆成的“上”字等内容,欢迎下载使用。
这是一份2022-2023学年河南省洛阳市涧西区八年级(下)期中数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









