08，河南省鹤壁市期中联考2023-2024学年八年级下学期4月期中数学试题

这是一份08，河南省鹤壁市期中联考2023-2024学年八年级下学期4月期中数学试题，共10页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的.
1.下列式子是分式的是（ ）
A.B.C.D.
2.芯片是一种把电路小型化并制造在一块半导体晶圆上的具有特殊功能的微型电路.芯片制造的核心是光刻技术，我国的光刻技术水平已突破到0.000000028m.将0.000000028用科学记数法表示为（ ）
A.B.C.D.
3.函数中自变量的取值范围是（ ）
A.B.且C.D.且
4.蝴蝶标本可以近似地看作轴对称图形，如图，将一只蝴蝶标本放在平面直角坐标系中，若图中点的坐标为，则其关于轴对称的点的坐标为（ ）
A.B.C.D.
5.小张同学在化简分式时得到的结果为，部分不小心用橡皮擦掉了，请你推测部分的代数式应该是（ ）
A.B.C.D.
6.若点，，都在反比例函数的图象上，则，，的大小关系是（ ）
A.B.C.D.
7.若，的值均扩大到原来的5倍，则下列分式的值保持不变的是（ ）
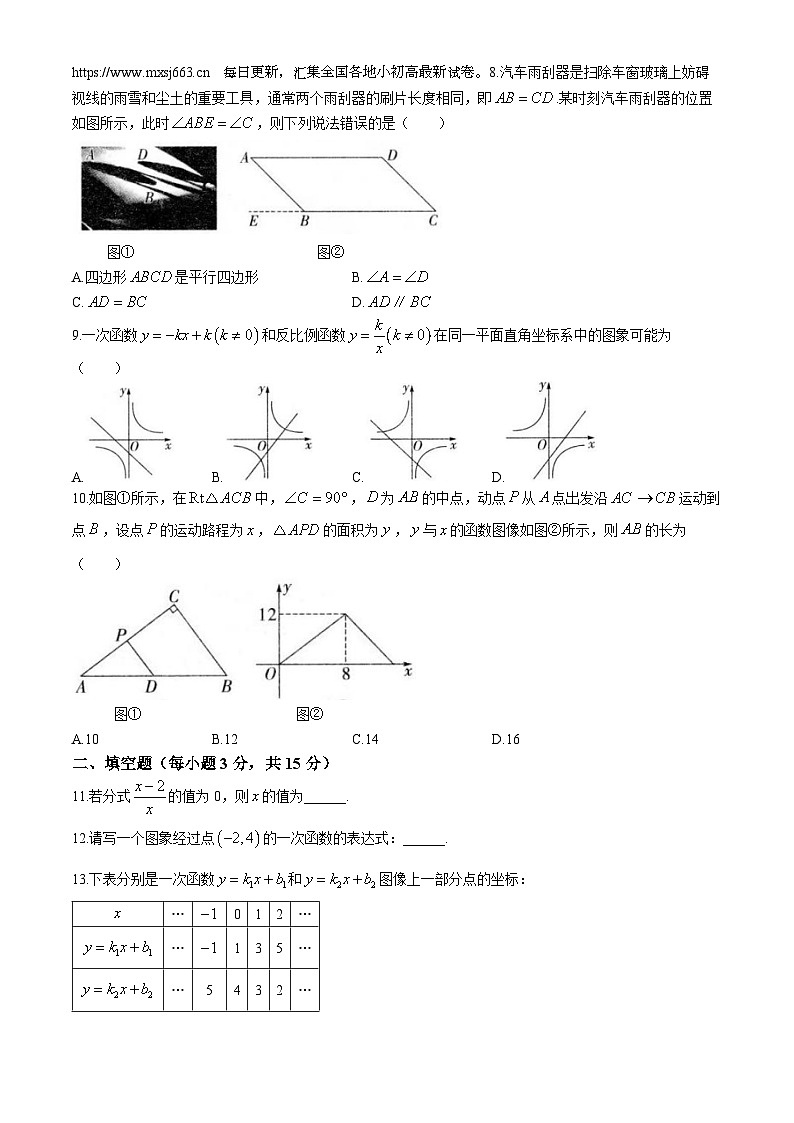
A.B.C.D.试卷源自 每日更新，汇集全国各地小初高最新试卷。8.汽车雨刮器是扫除车窗玻璃上妨碍视线的雨雪和尘土的重要工具，通常两个雨刮器的刷片长度相同，即.某时刻汽车雨刮器的位置如图所示，此时，则下列说法错误的是（ ）
图① 图②
A.四边形是平行四边形B.
C.D.
9.一次函数和反比例函数在同一平面直角坐标系中的图象可能为（ ）
A.B.C.D.
10.如图①所示，在中，，为的中点，动点从点出发沿运动到点，设点的运动路程为，的面积为，与的函数图像如图②所示，则的长为（ ）
图① 图②
A.10B.12C.14D.16
二、填空题（每小题3分，共15分）
11.若分式的值为0，则的值为______.
12.请写一个图象经过点的一次函数的表达式：______.
13.下表分别是一次函数和图像上一部分点的坐标：
则二元一次方程组的解为______.
14.如图，点在反比例函数的图象上，过点作轴的平行线交反比例函数的图象于点，点在轴上，若的面积为10，则的值为______.
15.如图，在平行四边形中，对角线，交于点，，过点作，交于点，交于点，连接，已知，，以点为原点建立坐标系，则点的坐标为______.
三、解答题（本大题共8个小题，共75分）
16.（10分）（1）计等：；
（2）先化简，再求值：，其中.
17.（9分）下面是小明同学解方程的过程，请认真阅读并完成任务.
任务一：横线处的内容为______，这一步的依据是______；
任务二：在老师的引导下，小明同学反思上述解答过程发现缺失了一步，请你补全这一步，并说明不能省略的理由；
任务三：请你根据平时的学习经验，就解分式方程还需要注意的事项给其他同学提一条建议.
18.（9分）甲、乙两车分别从、两地沿同一路线同时出发，相向而行，以各自的速度匀速行驶，甲车行驶到地停止，乙车行驶到地停止.甲、乙两车离地的距离、，与甲车行驶的时间之间的关系如图所示.
（1）、两地之间的距离为______km，经______h，甲车到达终点；
（2）求甲、乙两车各自的速度及，的值，并解释点的实际意义.
19.（9分）已知关于的分式方程.
（1）若分式方程无解，求的值；
（2）若分式方程的解为正数，求的取值范围.
20.（9分）如图，一次函数的图象与反比例函数的图象相交于，两点，与轴交于点.
（1）求反比例函数的解析式；
（2）当时，根据函数图像，求自变量的取值范围.
21.（9分）如图，四边形为平行四边形，连接，交于点，，分别为，的中点，连接，，.
（1）求证：；
（2）若，且，，求的长.
22.（10分）五一将至，某卖场欲购销一批电视机和空调，电视机和空调的进价和售价如下表：
（1）已知20万元购进电视机的数量与26万元购进空调的数量相同，求的值；
（2）若某单位准备从该卖场购买空调和电视机共50台，且空调数量不少于电视机的2倍，请求出最省钱的购买方案.
23.（10分）如图，一次函数的图象分别交轴，轴于点，，一次函数的图象分别交轴，轴于点，，两个一次函数的图像相交于点.
（1）求，的解析式；
（2）若直线上存在一点，使，求符合条件的点的坐标；
（3）若点为平面直角坐标系内任意一点，是否存在这样的点，使以，，，为顶点的四边形是平行四边形？若存在，请直接写出点的坐标；若不存在，请说明理由.
2023-2024学年下学期期中学业水平调研
八年级数学 参考答案
1.B
2.C 【解析】0.000000028用科学记数法表示为.
3.D 【解析】由题意得且，解得且.
4.A 【解析】点关于轴对称的点的坐标为.
5.B 【解析】将分式化简后得，.部分的代数式为.
6.A 【解析】，反比例函数的图象位于第一、三象限，且在每一象限内随的增大而减小.，.
7.C
8.B 【解析】，.又，四边形是平行四边形.，，，故选项B错误.
9.D 【解析】当时，反比例函数的图像在第一、三象限内，一次函数的图像经过第一、二、四象限，A选项和B选项不符合题意；当时，反比例函数的图象在第二、四象限内，一次函数的图像经过第一、三、四象限，C选项不符合题意，D选项符合题意.
10.A 【解析】由题图②可知，当时，面积最大，此时点运动到点，.此时，即，解得.在中，.
11.2
12.（答案不唯一）
13. 【解析】变形为，变形为，由题表可知，当时两个函数的值均为3，二元一次方程组的解为
14. 【解析】如解图，连接，，轴，，.
15. 【解析】四边形为平行四边形，，.，为等边三角形.，为边上的中线..在中，由勾股定理得，，，点的坐标为.
16.解：（1）原式
.…4分
（2）原式
.…4分
当时，原式.…6分
17.解：任务一：，等式的基本性质（分式的分子与分母乘（或除以）同一个不等于0的等式，分式的值不变；…2分
任务二：检验：当时，.理由：解分式方程可能产生增根，必须检验求出的解是否为增根（意思相近，逻辑合理即可）；…6分
任务三：去分母时，每一项都要乘最简公分母（答案不唯一，合理即可）.…9分
18.解：（1）360，6；…2分
【解法提示】由图像可得，、两地之间的距离为360km，经6小时，甲车到达终点.
（2）甲车速度：，乙车速度：，
，，
点的实际意义：当甲、乙两车行驶的时间为2.4h时，甲、乙两车相遇，离地的距离都为144km.…9分
19.解：（1）去分母，得，
移项、合并同类项，得.
分式方程无解，
①当方程有增根时，原方程无解，即，
，解得；
②当时，原方程无解，即.
综合①②，若分式方程无解，的值为或.…5分
（2）由（1）可得，
原分式方程的解为正数，
，.
，且.
且.…9分
20.解：（1）将点代入中，
得.点.
点在反比例函数的图象上，
，解得.
反比例函数的解析式为.…6分
（2）一次函数的图象与反比例函数的图象相交于，两点，令，
解得，.点的横坐标为.
当时，的取值范围即为当的图象在的图像下方时的取值范围.
由题图得的取值范围为或.…9分
21.（1）证明：在平行四边形中，对角线与交于点，
.
，分别为，的中点，
.
四边形是平行四边形，
，.
.
在和中，
.
.…5分
（2）解：由（1）得.
，.
为等腰三角形.
为的中点，.
，
在中，.
.…9分
22.解：（1）根据题意，得
，解得.
经检验，是原分式方程的解，且符合实际.
的值为2000.…4分
（2）设购买空调台，则购买电视机台.根据题意，
得，解得.
由（1）知，电视机售价为元，空调售价为元.
设总费用为元.则.
，，且为整数，当台时，最小.
此时（台）.
答：购买34台空调，16台电视机为最省钱的购买方案.…10分
23.解：（1）将代入，得，解得.
将代入，得，解得.
，的解析式分别为，.…3分
（2）对于，当时，；当时，.
点的坐标为，点的坐标为.
对于，当时，；当时，.
点的坐标为，点的坐标为.，..
设点的坐标为.
则.
，，即.
解得或.
符合条件的点的坐标为或.…7分
（3）存在，点的坐标为或或.…10分
【解法提示】如解图，由（1）（2）可知，，.设点的坐标为.
①当为对角线时，，，解得，.点的坐标为；
②当为对角线时，，，解得，.点的坐标为；
③当为对角线时，，，解得，.点的坐标为.综上所述，当点的坐标为或或时，以，，，为顶点的四边形是平行四边形.
…
0
1
2
…
…
1
3
5
…
…
5
4
3
2
…
解：方程两边同乘______，得，…第一步
去括号，得，…第二步
移项、合并同类项，得，…第三步
系数化为1，得，…第四步
是原分式方程的解.…第五步
电视机
空调
进价（元）
售价（元）