人教九年级数学 23.1 第2课时 旋转作图与坐标系中的旋转变换 PPT课件

这是一份人教九年级数学 23.1 第2课时 旋转作图与坐标系中的旋转变换 PPT课件，共29页。

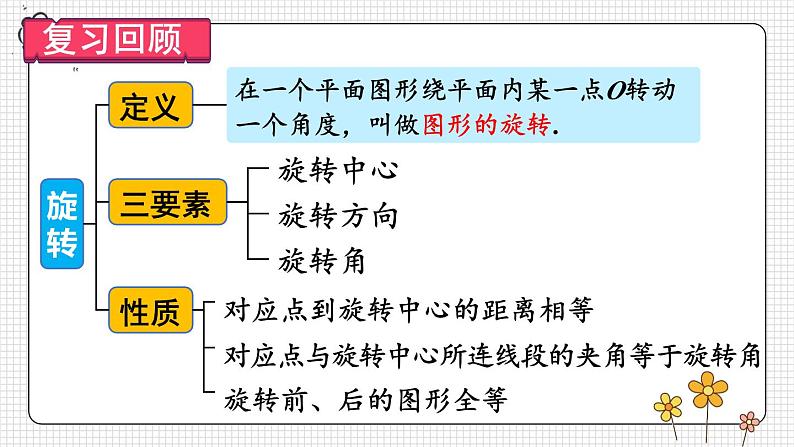
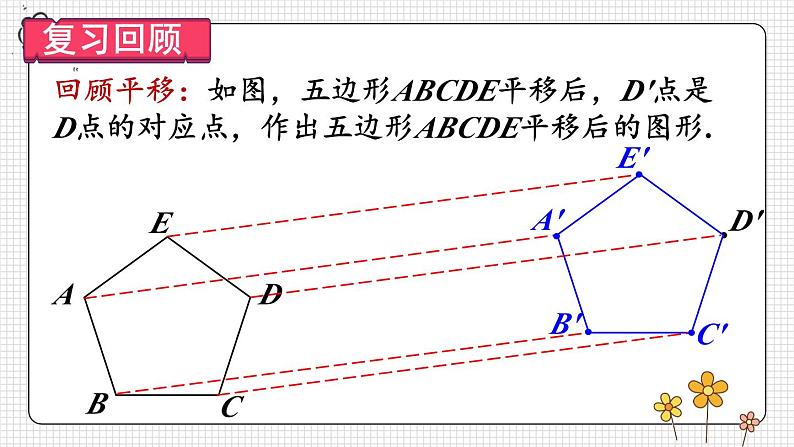
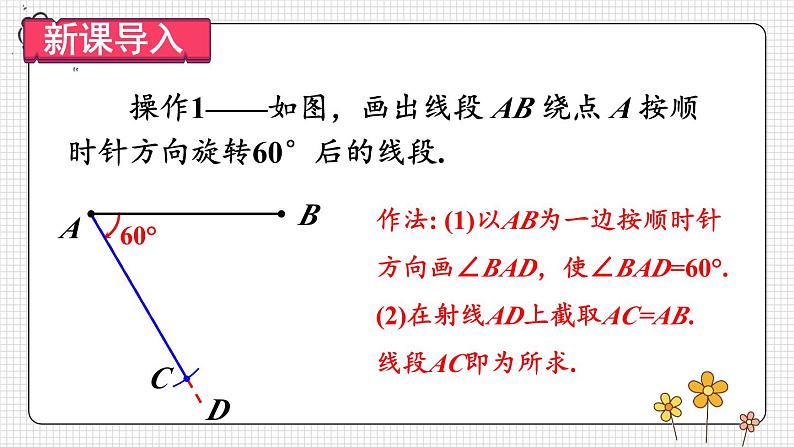
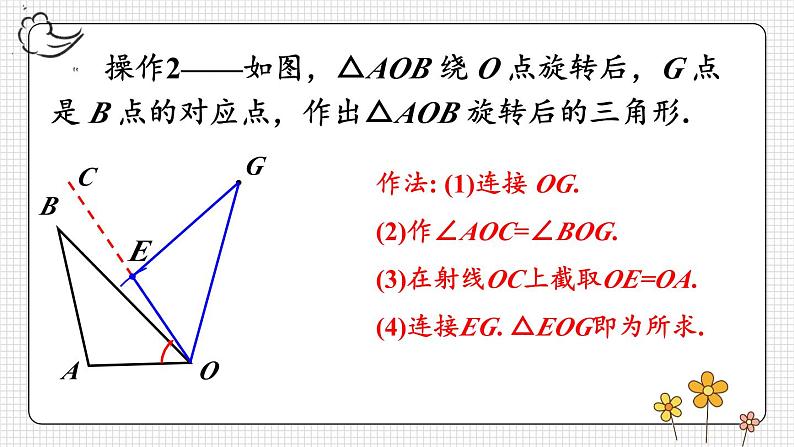
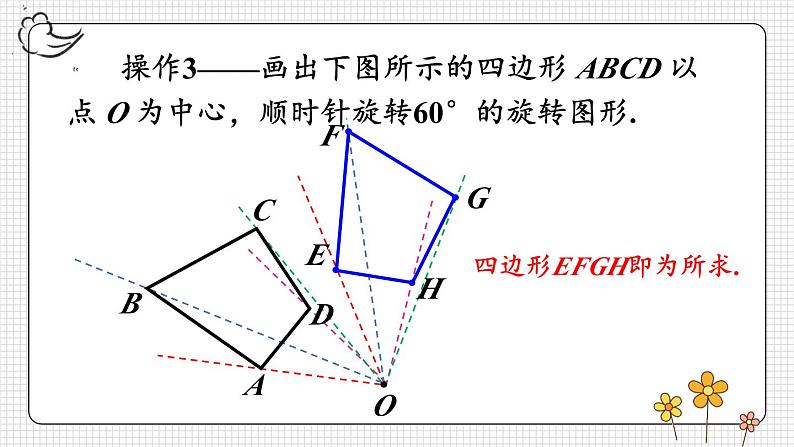
23.1 图形的旋转第2课时 旋转作图与坐标系中的旋转变换复习旋转及旋转图形的概念及基本性质，了解旋转作图的步骤和关键.掌握简单平面图形旋转的作法，能按要求作出简单平面图形旋转后的图形.体会旋转在图形变换中的作用，能利用旋转进行简单的图案设计.旋转回顾平移：如图，五边形ABCDE平移后，D'点是D点的对应点，作出五边形ABCDE平移后的图形.ABCDE 操作1——如图，画出线段 AB 绕点 A 按顺时针方向旋转60°后的线段.AB作法: (1)以AB为一边按顺时针方向画∠BAD，使∠BAD=60°.(2)在射线AD上截取AC=AB. 线段AC即为所求. 操作2——如图，△AOB 绕 O 点旋转后，G 点是 B 点的对应点，作出△AOB 旋转后的三角形.作法: (1)连接 OG.(2)作∠AOC=∠BOG.(3)在射线OC上截取OE=OA.(4)连接EG. △EOG即为所求. 操作3——画出下图所示的四边形 ABCD 以点 O 为中心，顺时针旋转60°的旋转图形.四边形EFGH即为所求.ABCDEFGH你能总结出旋转作图的一般步骤吗？举例：画出旋转后的三角形. 例 如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.确定点E的对应点E'A DB CE解：因为点A是旋转中心，所以它的对应点是 .正方形ABCD中，AD＝AB，∠DAB＝90°，所以旋转后点D与点 重合.B点A设点E的对应点为点E'. 因为旋转后的图形与旋转前的图形全等，所以∠ABE'=∠ADE=90°，BE'=DE.因此，在CB的延长线上取点E'，使BE'=DE，则△ABE'为旋转后的图形.E点的对应点E′，还可以用其他方法确定吗？方法一：由∠EAE′=90°，AE′=AE确定点E′.方法二：由∠ABE′=90°，AE′ =AE可知，以点A为圆心，AE为半径画弧，和CB的延长线的交点即是点E′.方法三：由∠ABE′=90°，∠EAE’=90°可知，过点A作AE垂直的直线与CB的延长线的交点即是E′. 任意画一个△ABC，以点A为旋转中心，把这个三角形逆时针旋转40°； 任意画一个△ABC，以AC中点为旋转中心，把这个三角形旋转180°. 选择不同的__________、不同的________旋转同一个图案，会出现不同的效果.旋转中心旋转角旋转中心不变，旋转角改变旋转角不变，旋转中心改变你还能通过旋转 设计出其他不同的图案吗？我们可以借助旋转设计出许多美丽的图案.【教材P62练习】把一个三角形进行旋转：(1)选择不同的旋转中心、不同的旋转角，看看旋转的效果;(2)改变三角形的形状，看看旋转的效果.旋转角不变,改变旋转中心(答案不唯一)旋转中心、旋转角都改变(答案不唯一)【教材P62练习】把一个三角形进行旋转：(1)选择不同的旋转中心、不同的旋转角，看看旋转的效果;(2)改变三角形的形状，看看旋转的效果. 1. 下面的图形是由一个基本的图形经过旋转得到的，分别指出它们的旋转中心和旋转角.【教材P63习题23.1 第5题】 2. △ABC中，AB=AC，P 是 BC 边上任意一点. 以点 A 为中心，取旋转角等于∠BAC，把△ABP逆时针旋转，画出旋转后的图形.【教材P62习题23.1 第3题】解：如图所示，△ACP'即为所求作的图形. 3. 分别画出△ABC绕点O逆时针旋转90°和180°后的图形.【教材P62习题23.1 第4题】解：旋转90°后的图形如图所示.旋转180°后的图形如图所示.4. 如图，△ABC中，∠C=90°.（1）将△ABC绕点B逆时针旋转90°，画出旋转后的三角形；（2）若BC=3，AC=4，点A旋转后的对应点为A，求A'A的长.【教材P63习题23.1 第9题】解：(1)△A'BC'即为所求.(2)∵△ABC中，∠C=90°，BC=3，AC=4.∴AB= =5. 由旋转的性质可得△A'BA 中，∠A'BA =90°，A'B=AB=5.∴A'A= . 5. 以原点为中心，把点A(4，5)逆时针旋转90°，得到点B. 求点B的坐标.【教材P63习题23.1 第11题】解：如图所示，画出旋转后的边OB.过点A作AC⊥x轴于点C.∵点A坐标为(4，5)，∴在Rt△ACO中，AC=5，OC=4.由题意知，△ACO绕点O逆时针旋转90°得到△BC'O，∴BC'=AC=5，OC'=OC=4.∵点B在第二象限，∴点B的坐标为(-5，4).旋转作图旋转中心旋转方向旋转角顺时针逆时针1.从课后习题中选取；2.完成练习册本课时的习题.