专题06 解答题压轴题（二次函数（面积及最值，实际应用））-2024年中考数学压轴题（安徽专用）

这是一份专题06 解答题压轴题（二次函数（面积及最值，实际应用））-2024年中考数学压轴题（安徽专用），文件包含专题06解答题压轴题二次函数二原卷版docx、专题06解答题压轴题二次函数二解析版docx等2份试卷配套教学资源，其中试卷共66页， 欢迎下载使用。


通用的解题思路：
一、利用二次函数求几何图形的面积及最值
1、根据已知条件得出抛物线解析式；
2、根据解析式，用公式法或配方法求出最值及取得最值时自变量的值及相应点的坐标、
二、实际问题与抛物线
1、从实际问题中抽象出二次函数模型；
2、数形结合解决实际问题，需要注意自变量的取值范围要使实际情况有意义。
1．（2022·安徽·中考真题）如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系xOy，规定一个单位长度代表1米．E（0，8）是抛物线的顶点．
(1)求此抛物线对应的函数表达式；
(2)在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点P1，P4在x轴上，MN与矩形P1P2P3P4的一边平行且相等．栅栏总长l为图中粗线段P1P2，，，MN长度之和．请解决以下问题：
（ⅰ）修建一个“”型栅栏，如图2，点P2，P3在抛物线AED上．设点P1的横坐标为m0（ⅱ）现修建一个总长为18的栅栏，有如图3所示的修建“”型或“”型栅型两种设计方案，请你从中选择一种，求出该方案下矩形P1P2P3P4面积的最大值，及取最大值时点P1的横坐标的取值范围（P1在P4右侧）．
【答案】(1)y＝−16x2＋8
(2)（ⅰ）l＝−12m2＋2m＋24，l的最大值为26；（ⅱ）方案一：最大面积27，−30＋9≤P1横坐标≤30；方案二：最大面积814＋92≤P1横坐标≤21
【分析】（1）通过分析A点坐标，利用待定系数法求函数解析式；
（2）（ⅰ）结合矩形性质分析得出P2的坐标为（m，－16m2＋8），然后列出函数关系式，利用二次函数的性质分析最值；
（ⅱ）设P2P1＝n，分别表示出方案一和方案二的矩形面积，利用二次函数的性质分析最值，从而利用数形结合思想确定取值范围．
【详解】（1）由题意可得：A（－6，2），D（6，2），
又∵E（0，8）是抛物线的顶点，
设抛物线对应的函数表达式为y＝ax2＋8，将A（－6，2）代入，
（－6）2a＋8＝2，
解得：a＝−16，
∴抛物线对应的函数表达式为y＝−16x2＋8；
（2）（ⅰ）∵点P1的横坐标为m（0＜m≤6），且四边形P1P2P3P4为矩形，点P2，P3在抛物线AED上，
∴P2的坐标为（m，−16m2＋8），
∴P1P2＝P3P4＝MN＝−16m2＋8，P2P3＝2m，
∴l＝3（−16m2＋8）＋2m＝−12m2＋2m＋24＝−12（m－2）2＋26，
∵−12＜0，
∴当m＝2时，l有最大值为26，
即栅栏总长l与m之间的函数表达式为l＝−12m2＋2m＋24，l的最大值为26；
（ⅱ）方案一：设P2P1＝n，则P2P3＝18－3n，
∴矩形P1P2P3P4面积为（18－3n）n＝－3n2＋18n＝－3（n－3）2＋27，
∵－3＜0，
∴当n＝3时，矩形面积有最大值为27，
此时P2P1＝3，P2P3＝9，
令−16x2＋8＝3，
解得：x＝±30，
∴此时P1的横坐标的取值范围为−30＋9≤P1横坐标≤30，
方案二：设P2P1＝n，则P2P3＝9－n，
∴矩形P1P2P3P4面积为（9－n）n＝－n2＋9n＝－（n－92）2＋814，
∵－1＜0，
∴当n＝92时，矩形面积有最大值为814，
此时P2P1＝92，P2P3＝92，
令−16x2＋8＝92，
解得：x＝±21，
∴此时P1的横坐标的取值范围为＋92≤P1横坐标≤21．
【分析】本题考查二次函数的应用，掌握待定系数法求函数解析式，准确识图，确定关键点的坐标，利用数形结合思想解题是关键．
2．（2023·山东青岛·中考真题）许多数学问题源于生活．雨伞是生活中的常用物品，我们用数学的眼光观察撑开后的雨伞（如图①）、可以发现数学研究的对象——抛物线．在如图②所示的直角坐标系中，伞柄在y轴上，坐标原点O为伞骨OA，OB的交点．点C为抛物线的顶点，点A，B在抛物线上，OA，OB关于y轴对称．OC=1分米，点A到x轴的距离是0.6分米，A，B两点之间的距离是4分米．

(1)求抛物线的表达式；
(2)分别延长AO，BO交抛物线于点F，E，求E，F两点之间的距离；
(3)以抛物线与坐标轴的三个交点为顶点的三角形面积为S1，将抛物线向右平移mm>0个单位，得到一条新抛物线，以新抛物线与坐标轴的三个交点为顶点的三角形面积为．若S2=35S1，求m的值．
【答案】(1)y=−0.1x2+1；
(2)10
(3)2或4；
【分析】（1）根据题意得到，A(2,0.6)，B(−2,0.6)，设抛物线的解析式为y=a(x−ℎ)2+k代入求解即可得到答案；
（2）分别求出AO，BO所在直线的解析式，求出与抛物线的交点F，E即可得到答案；
（3）求出抛物线与坐标轴的交点得到S1，表示出新抛物线找到交点得到，根据面积公式列方程求解即可得到答案；
【详解】（1）解：设抛物线的解析式为y=a(x−ℎ)2+k，由题意可得，
，A(2,0.6)，B(−2,0.6)，
∴ℎ=0，k=1，
把点A坐标代入所设解析式中得：4a+1=0.6，
解得：a=−0.1，
∴y=−0.1x2+1；
（2）解：设AO的解析式为：y=k1x，BO的解析式为：y=k2x，
分别将A(2,0.6)，B(−2,0.6)代入y=k1x，y=k2x得，
2k1=0.6，−2k2=0.6，
解得：k1=0.3，k2=−0.3，
∴AO的解析式为：y=0.3x，BO的解析式为：y=−0.3x，
联立直线解析式与抛物线得：0.3x=−0.1x2+1，
解得x1=−5，x2=2（舍去），
同理，解−0.3x=−0.1x2+1，得x3=5，x4=−2（舍去），
∴F(−5,−1.5)，E(5,−1.5)，
∴E，F两点之间的距离为：5−(−5)=10；
（3）解：当y=0时，−0.1x2+1=0，
解得：，
∴S1=12×10−(−10)×1=10，
∵抛物线向右平移mm>0个单位，
∴y=−0.1(x−m)2+1，
当x=0时，y=−0.1m2+1，
当y=0时，−0.1(x−m)2+1=0，解得：x=±10+m，
∴S2=12×10+m−(−10+m)×−0.1m2+1=10−0.1m2+1，
∵S2=35S1，
∴35×10=10−0.1m2+1，
解得：m1=2，（不符合题意舍去），m3=4，m4=−4（不符合题意舍去），
综上所述：m等于2或4；
【分析】本题考查二次函数综合应用，解题的关键是熟练掌握函数与坐标轴的交点求法及平移的规律：左加右减，上加下减．
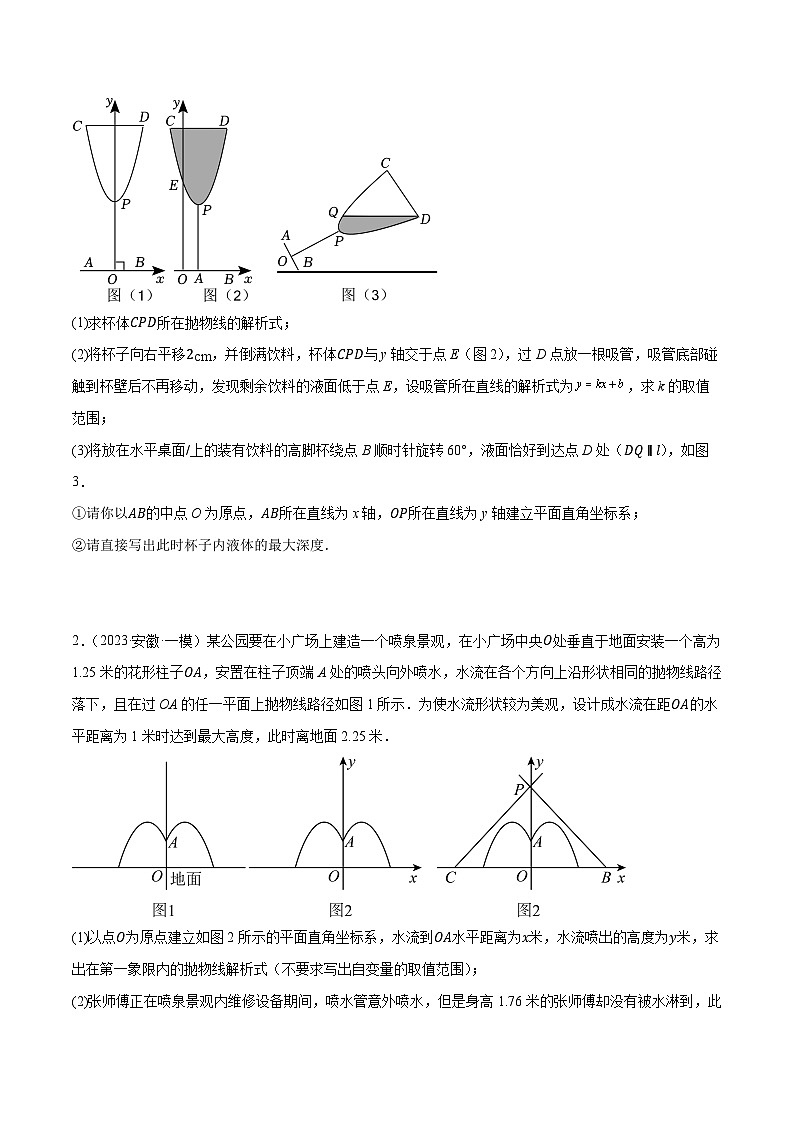
1．（2024·安徽合肥·二模）如图（1）是一个高脚杯的截面图，杯体CPD呈抛物线形（杯体厚度不计），杯底AB=23cm，点O是AB的中点，OP=CD=6cm，杯子的高度（即CD，AB之间的距离）为15cm，AB所在直线为x轴，OP所在直线为y轴建立平面直角坐标系（1个单位长度表示1cm）．
(1)求杯体CPD所在抛物线的解析式；
(2)将杯子向右平移2cm，并倒满饮料，杯体CPD与y轴交于点E（图2），过D点放一根吸管，吸管底部碰触到杯壁后不再移动，发现剩余饮料的液面低于点E，设吸管所在直线的解析式为，求k的取值范围；
(3)将放在水平桌面/上的装有饮料的高脚杯绕点B顺时针旋转60°，液面恰好到达点D处（DQ∥l），如图3．
①请你以AB的中点O为原点，AB所在直线为x轴，OP所在直线为y轴建立平面直角坐标系；
②请直接写出此时杯子内液体的最大深度．
【答案】(1)y=x2+6
(2)1(3)①M0,15−33，见解析；②398−332
【分析】（1）根据题意，得到P0,6，D3,15，设抛物线的解析式为y=ax2+b，代入计算即可；
（2）先确定平移后的解析式为y=x−22+6=x2−4x+10，再计算直线DE的解析式和直线DF的解析式，结合喝过一次饮料后，发现剩余饮料的液面低于点E，确定范围即可．
（3）①根据题意，画出符合题意的坐标系即可，设DQ与y轴的交点为M，计算OM的长即可得到坐标．
②设点N是抛物线上的一点，且Nn,n2+6，0≤n≤3；过点N作NG∥y轴，交DM于点G，过点G作GE⊥y轴于点E，确定Gn,3n+15−33，计算GN得最大值，且最大值为394−33，过点N作NH⊥MD于点H，则NH=12GN=398−332，
故NH的最大值为398−332．
【详解】（1）∵OP=CD=6cm，杯子的高度（即CD，AB之间的距离）为15cm．
∴P0,6，D3,15，
设抛物线的解析式为y=ax2+b，
∴9a+b=15b=6，
解得a=1b=6，
∴抛物线的解析式为y=x2+6．
（2）∵抛物线的解析式为y=x2+6，
∴平移后的解析式为y=x−22+6=x2−4x+10．
∴抛物线的对称轴为直线，E0,10，
∴E0,10的对称点为F4,10，
∵3,15，
∴平移后D5,15，
设直线DE的解析式为y=kx+10，
∴15=5k+10，
解得k=1；
∴y=x+10；
设直线DF的解析式为y=px+q，
∴5p+q=154p+q=10，
解得p=5q=−10；
∴y=5x−10，
根据题意，喝过一次饮料后，发现剩余饮料的液面低于点E，
∴1（3）①根据题意，建立直角坐标系如下，设DQ与y轴的交点为M，直线l与y轴的交点为S，
∵CD=6，杯子的高度（即CD，AB之间的距离）为15cm．
∴DT=CT=12CD=3，OT=15，
∵水平桌面/上的装有饮料的高脚杯绕点B顺时针旋转60°，
∴∠ABS=60°,∠OSB=30°，
∵DQ∥l，
∴∠TMD=∠OSB=30°，
∴TM=TDtan30°=33，
∴OM=OT−TM=15−33，
∴M0,15−33．
②∵抛物线的解析式为y=x2+6，
设点N是抛物线上的一点，且Nn,n2+6，0≤n≤3；
过点N作NG∥y轴，交DM于点G，
∵水平桌面/上的装有饮料的高脚杯绕点B顺时针旋转60°，
∴∠ABS=60°,∠OSB=30°，
∵DQ∥l，
∴∠TMD=∠OSB=30°，
过点G作GE⊥y轴于点E，
∵NG∥y轴，
∴GE=n，∠TMD=∠MGN=30°，
∴ME=GEtan30°=3n，
∴OE=OM+ME=3n+15−33，
∴Gn,3n+15−33，
∴GN=3n+15−33−n2−6
=−n2+3n+9−33
=−n−322+34+9−33
=−n−322+394−33，
∵，0≤32≤3，
∴n=32时，GN取得最大值，且最大值为394−33，
过点N作NH⊥MD于点H，
则NH=12GN=398−332，
故NH的最大值为398−332，
故液体的最大深度为398−332．
【分析】本题考查了待定系数法求解析式，正切函数的应用，构造二次函数求最值，特殊角的三角函数值，旋转的性质等，熟练掌握待定系数法，正切函数，构造二次函数求最值是解题的关键．
2．（2023·安徽·一模）某公园要在小广场上建造一个喷泉景观，在小广场中央O处垂直于地面安装一个高为1.25米的花形柱子OA，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上抛物线路径如图1所示．为使水流形状较为美观，设计成水流在距OA的水平距离为1米时达到最大高度，此时离地面2.25米．
(1)以点O为原点建立如图2所示的平面直角坐标系，水流到OA水平距离为x米，水流喷出的高度为y米，求出在第一象限内的抛物线解析式（不要求写出自变量的取值范围）；
(2)张师傅正在喷泉景观内维修设备期间，喷水管意外喷水，但是身高1.76米的张师傅却没有被水淋到，此时他离花形柱子OA的距离为d米，求d的取值范围；
(3)为了美观，在离花形柱子4米处的地面B、C处安装射灯，射灯射出的光线与地面成45°角，如图3所示，光线交汇点P在花形柱子OA的正上方，其中光线BP所在的直线解析式为y=−x+4，求光线与抛物线水流之间的最小垂直距离．
【答案】(1)y=−(x−1)2+2.25
(2)0.3(3)光线与抛物线水流之间的最小垂直距离为24米．
【分析】（1）根据题意得到第一象限内的抛物线的顶点坐标，将抛物线设成顶点式，再将点A坐标代入即可求出第一象限内的抛物线解析式；
（2）直接令y=1.76，解方程求出x的值，再根据函数的图象和性质，求出y>1.76时x的取值范围即可；
（3）先作辅助线，作出直线BP的平行线l，使它与抛物线相切于点D，然后设出直线l的解析式，联立直线与抛物线解析式，利用相切，方程只有一个解，解出直线l的解析式，从而得到直线与x轴交点，最后利用锐角三角函数求出直线l与直线BP之间的距离．
【详解】（1）根据题意第一象限内的抛物线的顶点坐标为(1,2.25)，A(0,1.25)，
设第一象限内的抛物线解析式为y=a(x−1)2+2.25，
将点A(0,1.25)代入物线解析式，
1.25=a(0−1)2+2.25，
解得a=−1，
∴第一象限内的抛物线解析式为y=−(x−1)2+2.25；
（2）根据题意，令y=1.76，
即−(x−1)2+2.25=1.76，
解得x1=0.3，x2=1.7，
∵−1<0，抛物线开口向下，
∴当0.31.76，
∴d的取值范围为0.3（3）作直线BP的平行线l，使它与抛物线相切于点D，分别交x轴，y轴于点E，F，过点E，作EG⊥PB，垂足为G，如图所示，
∵l∥PB，
设直线l的解析式为y=−x+m，
联立直线与抛物线解析式，
y=−x+my=−(x−1)2+2.25，
整理得x2−3x+m−1.25=0，
∵直线l与抛物线相切，
∴方程只有一个根，
∴Δ=32−4×1×(m−1.25)=0，
解得m=3.5，
∴直线l的解析式为y=−x+3.5，
令y=0，则x=3.5，
，
∴BE=4−3.5=0.5，
即EB=12，
∵射灯射出的光线与地面成45°角，
∴∠EBG=45°，
，
，
∴EG=22×12=24，
∴光线与抛物线水流之间的最小垂直距离为24米．
【分析】本题考查二次函数的应用，直线的平移，直线和抛物线相切等知识，关键是求抛物线解析式．
3．（2024·安徽宿州·一模）如图1，某洒水车的喷水口A距地面32m．如图2，已知喷水口喷出最远的水柱是抛物线C1：y1=ax−32+3，x轴是地面，OA位于y轴上，则点A0,32，抛物线C1与x轴交于点B．（注：抛物线水柱的宽度忽略）
(1)求该洒水车喷水能达到的最远距离OB的长；
(2)如图3，将抛物线C1向左平移使其经过点A，此时抛物线C2是该洒水车喷出的最近水柱，抛物线C2交x轴于点C．
（ⅰ）求OC的长；
（ⅱ）如图4，已知一条隔离绿化带的横截面是矩形DEFG，DG=1m，DE=2m，设洒水车到绿化带的距离，若该洒水车在行驶过程中能浇到完整的这条隔离绿化带，求d的取值范围．
【答案】(1)3+32；
(2)（ⅰ）32−3；（ⅱ）32−3≤d≤1+23．
【分析】
（1）根据抛物线过点A0,32，可得a的值，令y=0，解方程从而解决问题；
（2）（ⅰ）由对称轴知点A0,32的对称点为6,32，则下边缘抛物线是由上边缘抛物线向左平移6m得到的，可得OC的长度；
（ⅱ）根据DG=1m，，求出点F的坐标，利用增减性可得d的最大值和最小值，从而得出答案；
【详解】（1）解：∵抛物线过点A0,32，
∴32=a×0−32+3，
∴a=−16，
∴上边缘抛物线的函数解析式为y1=−16x−32+3，
令y1=0，则0=−16x−32+3，
解得x=3+32或x=−32+3（舍去），
∴洒水车喷出水的最大射程OB为3+32m；
（2）（ⅰ）∵y1对称轴为直线x=3，
∴点A0,32对称点为6,32，
∵平移后y2仍过点0,32，
是由y1向左平移6m得到的，
∵B3+32，0，点C是由点B向左平移6m得到的，
∴点C的坐标为3+32−6,0，即32−3,0，
∴OC=32−3；
（ⅱ）∵DG=EF=1m，
∴点F的纵坐标为1，
∴−16x−32+3=1，
解得x=3+23或x=3−23（舍去）
∴x=3+23，
当x>3时，y随x的增大而减小，
∴当3≤x≤3+32时，要使y≥1，
则x≤3+23，
∵当0≤x≤3时，y随x的增大而增大，且x=0时，y=32＞1，
∴当0≤x≤3+32时，要使y≥1，则0≤x≤3+23，
∵DE=2，灌溉车行驶时喷出的水能浇灌到整个绿化带，
∴OD的最大值为3+23−2=1+23
∵下边缘抛物线，喷出的水能灌溉到绿化带底部的条件是OD≥32−3，
∴OD的取值范围为32−3≤d≤1+23．
【分析】本题是二次函数的实际应用，主要考查了待定系数法求二次函数解析式，二次函数的性质，二次函数与方程的关系等知识，读懂题意，建立二次函数模型是解题的关键．
4．（2023·安徽·模拟预测）某蔬菜基地调洒水车来浇灌菜地，已知洒水的剖面是由AC、两条拋物线和地面组成，建立如图的平面直角坐标系．拋物线CND的函数表达式为y=−15x2+45x+1，拋物线AMB上点A的坐标为0,116，其最高点M离地面的高度是米，且恰好在点D的正上方．
(1)如图1，当时，求抛物线AMB与x轴正半轴的交点坐标．

(2)如图2，若大棚的一边是防风墙，防风墙距离点O有11米，墙高32米，要想所洒的水既能到墙边又不会洒到墙外，求的取值范围．

(3)如图3，在（2）抛物线AMB正好经过墙角Q的条件下，为了防止强光灼伤蔬菜，菜农将遮阴网（用线段PE表示，PE与拋物线AMB相交于点F）两端固定在P,E两处，点E距点O正好2米．若G是线段EF上一动点，过点G作GH⊥x轴交拋物线AMB于点，求GH长度的最大值．

【答案】(1)∴拋物线AMB与x轴正半轴的交点坐标为11,0
(2)
(3)米
【分析】（1）先求出点D的坐标，进而求出点M的坐标，设抛物线AMB的函数表达式为，把点A的坐标代入，求出抛物线AMB的函数表达式，最后令y=0，求出对的x的值即可；
（2）a=11150−125ℎ，则可求当x=11时，y=6625−1125ℎ，然后根据所洒的水既能到墙边又不会洒到墙外得出0≤6625−1125ℎ≤32，即可求解；
（3）先求直线EP的表达式为y=16x−13，抛物线的表达式为y=−16x2+53x+116，设点G的横坐标为m，则∴GH=yH−yG=−16m2+32m+136=−16m−922+13324，然后根据二次函数的性质求解即可．
【详解】（1）解：把y=0代入y=−15x2+45x+1，得，
解得x1=−1,x2=5，
∴点D的坐标为5,0，
∴抛物线AMB的顶点M的坐标为5,6．
设抛物线AMB的函数表达式为．
将点A0,116代入，得，解得a=−16，
∴抛物线AMB的函数表达式为y=−16(x−5)2+6．
令y=0，得−16(x−5)2+6=0，
解得，
∴拋物线AMB与x轴正半轴的交点坐标为11,0．
（2）解：设抛物线AMB的函数表达式为．
∵它经过点A0,116，
∴a0−52+ℎ=116，
，
当x=11时，y=a11−52+ℎ=36a+ℎ=3611150−125ℎ+ℎ=6625−1125ℎ．
∵要想所洒的水既能到墙边又不会洒到墙外，
，
解得，
∴ℎ的取值范围为．
设抛物线AMB的函数表达式为，把点A坐标代入，求出
（3）解：由题意知，点E的坐标为2,0，点P的坐标为．
设EP所在直线的函数表达式为，
∴2k+b=0，11k+b=32，解得k=16，b=−13，
．
∵拋物线AMB正好经过墙角Q，
∴抛物线AMB的函数表达式为y=−16x−52+6=−16x2+53x+116．
设点G的横坐标为m．
∵GH⊥x轴，∴点的横坐标为m．
．
∵−16<0，
∴当m=92时，GH取最大值，
即GH长度的最大值为米．
【分析】本题考查了二次函数的实际应用，待定系数法，二次函数的性质，线段长度问题等知识，明确题意，运用方程思想与数形结合思想是解题的关键．
5．（2023·浙江湖州·中考真题）如图1，在平面直角坐标系xOy中，二次函数y=x2−4x+c的图象与y轴的交点坐标为0,5，图象的顶点为M．矩形ABCD的顶点D与原点O重合，顶点A，C分别在x轴，y轴上，顶点B的坐标为1,5．

(1)求c的值及顶点M的坐标，
(2)如图2，将矩形ABCD沿x轴正方向平移t个单位0①当t=2时，求QG的长；
②当点G与点Q不重合时，是否存在这样的t，使得△PGQ的面积为1？若存在，求出此时t的值；若不存在，请说明理由．
【答案】(1)c=5，顶点M的坐标是2,1
(2)①1；②存在，t=12或52
【分析】（1）把0,5代入抛物线的解析式即可求出c，把抛物线转化为顶点式即可求出顶点坐标；
（2）①先判断当t=2时，D'，A'的坐标分别是2,0，3,0，再求出x=3，时点Q的纵坐标与点P的纵坐标，进而求解；
②先求出QG=2，易得P，Q的坐标分别是t,t2−4t+5，t+1,t2−2t+2，然后分点G在点Q的上方与点G在点Q的下方两种情况，结合函数图象求解即可．
【详解】（1）∵二次函数y=x2−4x+c的图象与y轴的交点坐标为0,5，
∴c=5，
∴y=x2−4x+5=x−22+1，
∴顶点M的坐标是2,1．
（2）①∵A在x轴上，B的坐标为1,5，
∴点A的坐标是1,0．
当t=2时，D'，A'的坐标分别是2,0，3,0．
当x=3时，y=3−22+1=2，即点Q的纵坐标是2，
当时，y=2−22+1=1，即点P的纵坐标是1．
∵PG⊥A'B'，
∴点G的纵坐标是1，
∴QG=2−1=1．
②存在．理由如下：
∵△PGQ的面积为1，PG=1，
∴QG=2．
根据题意，得P，Q的坐标分别是t,t2−4t+5，t+1,t2−2t+2．
如图1，当点G在点Q的上方时，QG=t2−4t+5−t2−2t+2=3−2t=2，
此时t=12（在0
如图2，当点G在点Q的下方时，QG=t2−2t+2−t2−4t+5=2t−3=2，
此时t=52（在0∴t=12或52．
【分析】本题考查了二次函数图象上点的坐标特点、矩形的性质以及三角形的面积等知识，熟练掌握二次函数的图象与性质、灵活应用数形结合思想是解题的关键．
6．（2022·河北保定·二模）如图，某跳水运动员进行10米跳台跳水训练，水面边缘点E的坐标为−32,−10．运动员（将运动员看成一点）在空中运动的路线是经过原点O的抛物线．在跳某个规定动作时，运动员在空中最高处A点的坐标为1,54，正常情况下，运动员在距水面高度5米以前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误．运动员入水后，运动路线为另一条抛物线．

(1)求运动员在空中运动时对应抛物线的解析式并求出入水处B点的坐标；
(2)若运动员在空中调整好入水姿势时，恰好距点E的水平距离为5米，问该运动员此次跳水会不会失误？通过计算说明理由；
(3)在该运动员入水点的正前方有M，N两点，且EM=212，EN=272，该运动员入水后运动路线对应的抛物线解析式为y=a（x−ℎ）2+k，且顶点C距水面4米，若该运动员出水点D在MN之间（包括M，N两点），请直接写出a的取值范围．
【答案】(1)y=−54x−12+54；4，−10
(2)该运动员此次跳水失误了，理由见解析
(3)14≤a≤1625
【分析】（1）设抛物线的解析式为y=a0x−12+54，将0,0代入即可求得解析式；令y=−10，即可求得点B的坐标；
（2）求出距点E水平距离为5米的点的纵坐标即可进行判断；
（3）分别求出当抛物线经过点M、N时的a的值即可．
【详解】（1）解：设抛物线的解析式为y=a0x−12+54
将0,0代入解析式得：a0=−54
∴抛物线的解析式为y=−54x−12+54
令y=−10，则−10=−54x−12+54
解得：x1=−2(舍去),x2=4
∴入水处B点的坐标4，−10
（2）解：距点E的水平距离为5米，对应的横坐标为：x=5−32=72
将x=72代入解析式得：y=−54×72−12+54=−10516
∵−10516−−10=5516<5
∴该运动员此次跳水失误了
（3）解：∵EM=212，EN=272，点E的坐标为−32,−10
∴点M、N的坐标分别为：9,−10,12,−10
∵该运动员入水后运动路线对应的抛物线解析式为y=a（x−ℎ）2+k，顶点C距水面4米
y=ax−1322−14，
∴当抛物线经过点M时，把点M9,−10代入得：a=1625
同理，当抛物线经过点12,−10时，a=14
由点D在MN之间可得：14≤a≤1625
【分析】本题考查了二次函数在实际生活中的应用．涉及了抛物线的顶点式、求抛物线上的点的坐标等．熟记二次函数的相关形式是解题关键．
7．（2023·安徽亳州·模拟预测）如图，某小区的景观池中安装一雕塑OA，OA=2米，喷出两股水流，两股水流可以抽象为平面直角坐标系中的两条抛物线（图中的C1，C2）的部分图象，两条抛物线的形状相同且顶点的纵坐标相同，且经测算发现抛物线C2的最高点（顶点）C距离水池面2.5米，且与OA的水平距离为2米．

(1)求抛物线C2的解析式；
(2)求抛物线C1与x轴的交点B的坐标；
(3)小明同学打算操控微型无人机在C1，C2之间飞行，为了无人机的安全，要求无人机在竖直方向上的活动范围不小于0.5米，设无人机与OA的水平距离为m，求m的取值范围．
【答案】(1)y=−18x2+12x+2；
(2)y=−18x2−12x+2，；
(3)12≤m≤6
【分析】（1）由题意可知C2过点和点C(2,2.5)，且−b2a=2，代入解析式可求得解析式；
（2）两条抛物线的形状相同且顶点的纵坐标相同且C1经过点，设C1的解析式为，代入相关数据即可求得解析式，再根据题意进行取舍即可；
（3）无人机的横坐标为x，根据题意列出不等式−18x2+12x+2−−18x2−x+2≥0.5，求解即可．
【详解】（1）解：由已知可得：C2过点和点C(2,2.5)，设其解析式为y=ax2+bx+c，
代入两点，由C的横坐标为−b2a=2可得，
c=24a+2b+c=2.5−b2a=2，解得：a=−18b=12c=2，
故C2的解析式为：y=−18x2+12x+2；
（2）解：∵两条抛物线的形状相同，
∴设C1的解析式为y=−18x2+b1x+c1，
已知C1经过点，故C1的解析式为y=−18x2+b1x+2①，
∵顶点的纵坐标相同，
的顶点的横坐标为4b1，代入①，
可得：−18⋅4b12+b1⋅4b1+2=2.5，
解得：b1=±12，
故C1的解析式为y=−18x2+12x+2②或y=−18x2−12x+2③，
由图可知C1的终点的横坐标小于0，而②中−b2a=2>0不合题意，故舍去②，
令将y=0代入y=−18x2−12x+2，
解得x=−2+25或−2−25（舍去），
故B点的坐标为；
（3）解：由题意可得：−18m2+12m+2−−18m2−12n+2≥0.5，
解得：m≥12，
又∵−18m2+12m+2≥0.5，
解得：m≤6，
12≤m≤6．
【分析】本题考查二次函数的应用，根据题意正确求出函数的解析式是解题关键．
8．（2023·安徽芜湖·二模）某大型乐园包含多项主题演出与游乐项目，其中过山车“冲上云霄”是其经典项目之一．如图所示，A→B→C为过山车“冲上云霄”的一部分轨道（B为轨道最低点），它可以看成一段抛物线．其中OA=1254米，OB=252米（轨道厚度忽略不计）．
(1)求抛物线A→B→C的函数关系式；
(2)在轨道距离地面5米处有两个位置P和C，当过山车运动到C处时，又进入下坡段C→E （接口处轨道忽略不计）．已知轨道抛物线C→E→F的大小形状与抛物线A→B→C完全相同，求OE的长度；
(3)现需要对轨道下坡段A→B进行安全加固，架设某种材料的水平支架和竖直支架GD、GM、HI、HN，且要求OM=MN． 如何设计支架，可使得所需用料最少？最少需要材料多少米？
【答案】(1)
(2)452
(3)当OM=MN=6时用料最少，最少需要材料532米
【分析】（1）用待定系数法求函数解析式即可；
（2）先求出P，C坐标，再求出PC长度，通过抛物线C→E→F的形状与抛物线A→B→C完全相同，平移长度为PC，可得抛物线C→E→F解析式，可得结论；
（3）先设出M，N横坐标，再代入解析式，分别求出G，的纵坐标，然后求出GD、GM、HI、HN之和的最小值，从而求出最少所需材料．
【详解】（1）解：由图象可设抛物线解析式为：，
把代入，得：，
解得：a=15，
∴抛物线A→B→C的函数关系式为；
（2）当y=5时，，
解得：x1=152，x2=352，
，5)，，5)，
，
∵抛物线C→E→F的形状与抛物线A→B→C完全相同，
∴抛物线C→E→F由抛物线A→B→C右平移PC个单位，
∴抛物线C→E→F为：，
当y=0时，x=452，
；
（3）设OM=MN=m，M(m,0)，，
，，
，
，
∴开口向上，
∴当m=6时，l最短，最短为532米，
即当OM=MN=6时用料最少，最少需要材料532米．
【分析】本题考查二次函数的应用以及平移的性质，关键用抛物线的性质解决实际问题．
9．（2023·安徽蚌埠·二模）如图，蚌埠花博园要建造一圆形喷水池，在水池中央垂直于水面安装一个柱子OA，O恰在水面中心，OA高3米，如图1，由柱子顶端处的喷头向外喷水，水流在各方面沿形状相同的抛物线落下．
(1)如果要求设计成水流在离OA距离为1米处达到最高点，且与水面的距离是4米，那么水池的内部半径至少要多少米，才能使喷出的水不致落到池外；（利用图2所示的坐标系进行计算）
(2)若水流喷出的抛物线形状与（1）相同，水池内部的半径为5米，要使水流不落到池外，此时水流达到的最高点与水面的距离应是多少米？
【答案】(1)水池的内部半径至少要3米
(2)19625米
【分析】（1）设抛物线的解析式为y=ax−12+4，待定系数法，求出函数解析式，求出y=0时的x的值，即可得解；
（2）设抛物线的解析式为y=−x2+bx+c，待定系数法求出解析式，将解析式转化为顶点式，即可得出结论．
【详解】（1）解：∵水流在离OA距离为1米处达到最高点，且与水面的距离是4米，
∴设抛物线的解析式为y=ax−12+4，由题意，得：抛物线过点0,3，
∴3=a+4，解得：a=−1，
∴y=−x−12+4．
当y=0时，
0=−x−12+4，
解得：x1=−1（舍去），x2=3．
∴水池的内部半径至少要3米；
（2）根据水流喷出的抛物线形状与（1）相同，得到新的抛物线解析式的a=−1，
设抛物线的解析式为y=−x2+bx+c，由题意，得：抛物线过点0,3,5,0，
∴0=−25+5b+c3=c，
解得：b=225c=3，
∴y=−x2+225x+3=−x−1152+19625，
∴此时水流达到的最高点与水面的距离应是19625米．
【分析】本题考查二次函数的实际应用．正确的求出二次函数的解析式，利用二次函数的性质进行求解，是解题的关键．
10．（2023·安徽合肥·二模）如图1所示的某种发石车是古代一种远程攻击的武器，将发石车置于山坡底部O处，以点O为原点，水平方向为x轴方向，建立如图2所示的平面直角坐标系，将发射出去的石块当作一个点看，其飞行路线可以近似看作抛物线y=ax−202+k的一部分，山坡OA上有一堵防御墙，其竖直截面为ABCD，墙宽BC=2米，BC与x轴平行，点B与点O的水平距离为28米、垂直距离为6米．
(1)若发射石块在空中飞行的最大高度为10米，
①求抛物线的解析式；
②试通过计算说明石块能否飞越防御墙；
(2)若要使石块恰好落在防御墙顶部BC上（包括端点B、C），求a的取值范围，
【答案】(1)y=−140x2+x；②石块能飞越防御墙；
(2)−150≤a≤−156
【分析】（1）①根据题意得抛物线解析式为：y=ax−202+10，待定系数法求解析式即可求解；
②根据题意，得出B28,6，将x=28代入解析式计算，即可求解．
（2）依题意得出C30,6，进而根据B,C以及原点分别待定系数法求解析式即可求解．
【详解】（1）解：①∵发射石块在空中飞行的最大高度为10米，
∴抛物线解析式为：y=ax−202+10，
将点0,0代入得，202a+10=0，
解得：a=−140，
∴抛物线解析式为y=−140x−202+10=−140x2+x，
∴y=−140x2+x，
②∵点B与点O的水平距离为28米、垂直距离为6米．
∴B28,6，
当x=28时，y=−140×282+28=8.4>6，
∴石块能飞越防御墙；
（2）∵BC=2，B28,6，
∴C30,6
当y=ax−202+k经过点B28,6，0，0时，
202a+k=082a+k=6，解得：a=−156.
当y=ax−202+k经过点C30,6，0，0时，
202a+k=0102a+k=6，解得：a=−150
∴要使石块恰好落在防御墙顶部BC上（包括端点B、C），a的取值范围为−150≤a≤−156
【分析】本题考查了二次函数的实际应用，熟练掌握待定系数法求解析式是解题的关键．
11．（2023·安徽亳州·模拟预测）万达乐园的过山车是其经典项目之一．如图，B→D→C为过山车的—部分轨道，若这部分轨道可以用抛物线y=ax−ℎ2+10来刻画，点B到y轴的水平距离AB=4米，点B到工轴（代表地面）的距离BE=6米，B，C间的水平距离为12米．
(1)求抛物线BDC的函数表达式．
(2)当过山车运动到C处时，平行于地面向前运动了2米至H点，又进入下一段轨道H→F→G．已知轨道H→F→G的形状与轨道B→D→C完全相同，若某名游客从B→D→C轨道滑行至H→F→G轨道，起点和终点距离地面均为8米，则该游客移动的最大水平距离是多少？（结果保留根号）
(3)已知轨道B→M→N→C和轨道B→D→C关于BC对称，现需要在轨道B→M→N→C下进行安全加固，建造支架PM,QN，且EP=PQ，支架的价格是20000元/米，如何设计支架，使得造价最低？最低造价为多少元？
【答案】(1)y=−19x2+209x−109
(2)14+62米
(3)两个支架相距3.6米时，造假最低为96000元
【分析】（1）根据题意确定B4,6,C16,6，即可得出抛物线的对称轴，然后将点B代入解析式即可求解；
（2）根据题意分析：当游客最开始实在BD段上距离地面8米，最后位置是在FG段上距离地面8米处停下时，水平移动的距离最大，然后确定出抛物线HFG的解析式，再代入求解即可；
（3）根据题意确定抛物线BMNC解析式为y=19x−102+2，设点P4+a,0，则点Q4+2a,0(0【详解】（1）解：∵B到y轴的水平距离AB=4米，点B到工轴（代表地面）的距离BE=6米，B，C间的水平距离为12米．
∴B4,6,C16,6，
∴抛物线的对称轴为：x=4+162=10=ℎ，
∴抛物线的解析式为：y=ax−102+10
将点B代入抛物线解析式y=ax−ℎ2+10得：
6=a4−102+10，
解得：a=−19，
∴抛物线的解析式为y=−19x−102+10=−19x2+209x−109；
（2）解：当游客最开始实在BD段上距离地面8米，最后位置是在FG段上距离地面8米处停下时，水平移动的距离最大，
当y=8时，在抛物线BDC段上，8=−19x−102+10，
解得：x1=10−32,x2=10+32（不符合题意，舍去），
∵B，C间的水平距离为12米，过山车运动到C处时，平行于地面向前运动了2米至H点，
∴抛物线HFG为抛物线BDC向右平移12+2=14个单位长度后的图象，
∴抛物线HFG的解析式为：y=−19x−10−142+10=−19x−242+10，
当y=8时，在抛物线HFG段上，8=−19x−242+10，
解得：x1=24+32,x2=24−32（不符合题意，舍去），
∴该游客移动的最大水平距离为：24+32−10−32=14+62米；
（3）解：由（1）得抛物线BDC的顶点坐标为10,10，
∴点D到BC的距离为10−6=4米，
设点P4+a,0，则点Q4+2a,0(0∵抛物线BDC与抛物线BMNC关于BC对称，
∴抛物线BMNC的顶点坐标为10,6−4即10,2
∴抛物线BMNC解析式为y=19x−102+2，
将点P和点Q的横坐标代入解析式得：yM=194+a−102+2，yN=194+2a−102+2，
∴PM+QN=yM+yN=59a2−4a+12，
关于a的方程的对称轴为a=3.6，
当a=3.6时，PM+QN取得最小值，
∴PM+QN=59×3.62−4×3.6+12=4.8，
∴最低造价为4.8×20000=96000元，
∴两个支架相距3.6米时，造假最低为96000元．
【分析】本题考查了二次函数的应用，熟练掌握二次函数的图象与性质、正确理解题意是解题的关键．
12．（2023·安徽合肥·二模）如图，某数学兴趣小组以楼梯为场景设计的小球弹射实验示意图，楼梯平台AB宽为3，AB前方有六个台阶T1~T6（各拐点均为90°），每个台阶的高为2，宽为2，楼梯平台到x轴距离OA=14，从y轴上的点C处向右上方弹射出一个小球P（小球视为点），飞行路线为抛物线L:y=−12x2+2x+16，当点P落到台阶后立即弹起，其飞行路线是与L形状相同的抛物线．
(1)通过计算判断小球P第一次会落在哪个台阶上；
(2)若小球P第二次的落点在台阶T5中点M上，求小球P第二次飞行路线的解析式；
(3)若小球P再次从点M处弹起后落入x轴上一圆柱形小球接收装置（小球落在圆柱形边沿也为接收），接收装置最大截面为矩形，点E横坐标为16，EF=1，EH=1，求出小球第三次飞行路线的顶点到x轴距离最小值．
【答案】(1)T2台阶上．
(2)y=−12x2+8x−20
(3)15332
【分析】（1）根据题意，第二个台阶的左端点坐标为5,10，右端点坐标为7,10，计算x=5，x=7时的y值，运用夹逼法确定交点位置．
（2）根据（1）得到P的起点坐标为6,10，再次着地左端点横坐标为x=3+2×5−1=11，纵坐标为y=14−2×5=4，结合台阶宽为2，得到点P的落地点坐标为12,4，设解析式求解即可．
（3）根据（2）得到P的起点坐标为12,4，再次着地近地点坐标为16,1，远地点坐标为17,1，设解析式求解即可．
【详解】（1）∵楼梯平台AB宽为3，每个台阶的高为2，宽为2，OA=14，
∴第二个台阶的左端点坐标为5,10，右端点坐标为7,10，
当x=5时，y=−12×25+10+16=13.5＞10；
当x=7时，y=−12×49+14+16=5.5＜10；
故与抛物线交点在5,10， 7,10之间，
当y=10时，−12×x2+2x+16=10，
解得x=6,x=−2（舍去）
∴小球落在第二个台阶上，此时点P6,10．
（2）根据（1）得到P的起点坐标为6,10，再次着地左端点横坐标为x=3+2×5−1=11，纵坐标为y=14−2×5=4，结合台阶宽为2，得到点P的落地点坐标为12,4，
设解析式y=−12x2+bx+c，
得−12×36+6b+c=10−12×144+12b+c=4，
解得b=8c=−20．
故解析式为y=−12x2+8x−20．
（3）根据（2）得到P的起点坐标为12,4，近地点坐标为16,1，
设解析式y=−12x2+bx+c，
得−12×256+16b+c=1−12×144+12b+c=4，
解得b=534c=−83．
故解析式为y=−12x2+534x−83，
此时，函数的最小值为4ac−b24a=4×−12×−83−53424×−12=15332．
根据（2）得到P的起点坐标为12,4，远地点坐标为17,1，
设解析式y=−12x2+bx+c，
得−12×289+17b+c=1−12×144+12b+c=4，
解得b=13910c=−90810．
故解析式为y=−12x2+13910x−90810，
此时，函数的最小值为4ac−b24a=4×−12×−90810−1391024×−12=1161200．
∵15332＜1161200，
∴小球第三次飞行路线的顶点到x轴距离最小值是15332．
【分析】本题考查了二次函数的应用，待定系数法求解析式，求函数的最值，熟练掌握待定系数法，抛物线的最值是解题的关键．
13．（2023·河北唐山·一模）为了给观光绿化带浇水，拟安装一排喷水口，如图2 为喷水口喷水的横截面，该喷水口 离地竖直高度 OH 为 1.5m，可以把喷出水的上、下边缘抽象为两条抛物线的部分图象：把绿化带横截面抽象为矩形DEFG，其中 DE=2m,EF=0.5m，其下边缘抛物线是由上边缘抛物线向左平移得到，上边抛物线最高点 A 离喷水口的水平距离为2m，高出喷水口0.5m， 喷水口到绿化带的水平距离OD 为d（单位： ）．
(1)求上边缘抛物线的函数解析式，并求喷出水的最大射程OC；
(2)通过计算求点B的坐标；
(3)绿化带右侧（图中点E的右侧）1米外是人行道，要使喷出的水能浇灌到整个绿化带，同时不会淋湿行人，直接写出d的取值范围．
【答案】(1)y=−18x−22+2，OC=6米；
(2)B2,0
(3)3≤d≤23
【分析】本题是二次函数的实际应用，
（1）由题意可知：顶点坐标A2,2，，利用待定系数法即可求出函数解析式为：y=−18x−22+2，令即可求出OC=6米；
（2）利用关于对称轴的对称点为：4,1.5，可知下边缘抛物线是由上边缘抛物线向左平移4个单位得到，求出下边缘抛物线为：，进一步可求出B2,0，即可求解．
（3）当点，d有最小值，此时d=3；当上边缘抛物线过点F时，d有最大值，d=2+23−2=23；所以3≤d≤23．
【详解】（1）解：由题意可知：A2,2，故设上边缘抛物线的函数解析式为：y=ax−22+2，
∵，
将其代入y=ax−22+2可得：，解得：a=−18，
∴上边缘抛物线的函数解析式为：y=−18x−22+2，
令，解得：x=6或x=−2，
∵点C在x轴的正半轴，
∴C6,0，即喷出水的最大射程OC=6米．
（2）解：∵关于对称轴的对称点为：4,1.5，
∴下边缘抛物线是由上边缘抛物线向左平移4个单位得到，
∴下边缘抛物线为：，
令，解得：x=−6或，
∵点B在正半轴上，
∴B2,0．
（3）解：绿化带右侧（图中点E的右侧）1米外是人行道，
此时EC=1
则DC=2+1=3，
当d有最小值，d=OC−CD=3
当上边缘抛物线过点F时，d有最大值，
∵DE=2m，EF=0.5m．
∴令，解得：x=2+23或x=2−23，
结合图象可知：
∴d的最大值为：d=2+23−2=23；
∴3≤d≤23．
14．（2024·浙江杭州·模拟预测）
【答案】任务1：y=−59x+72+5
任务2：OP的高度为585米
任务3：215【分析】本题考查了二次函数在实际问题中的应用，
任务1：以点O为原点建立如图所示直角坐标系，设出抛物线的顶点式，再将−10,0代入即可得到结论；
任务2：令（1）抛物线y=1.8，得x=−4.6，求出FM=1.4，再依据GM:FM=2:7即可得出点G的坐标为−4.2,1.8，设图3中抛物线解析式为y=−59x2+d，代入即可求解．
任务3；设P0,m，根据题意得从点喷射的抛物线水柱顶点坐标为k,m+0.8，由于抛物线形状相同，可得抛物线表达式为y=−59x−k2+m+0.8，把P0,m代入可得k=−1.2，可得函数关系式，再把点M−4.6,1.8代入即可得出结论．
【详解】解：任务1：以O为原点，AB所在直线为x轴建立直角坐标系，如图1所示．
∵AB=20，
∴．
∵水柱距水池中心7m处到达最高，高度为5m，
∴左侧抛物线顶点为(−7,5)，
设抛物线解析式为y=ax+72+5，
把代入得a=−59，
∴y=−59x+72+5即y=−59x2−709x−2009．
任务2：如图所示，以O为原点，AB所在直线为x轴建立直角坐标系
∵两种喷水头均能喷射与图2中形状相同的抛物线．
设OP的最高高度为m．
∴设图3中抛物线解析式为y=−59x2+d
由（1）可得图2中的抛物线解析式为:y=−59x+72+5
令y=1.8，得1.8=−59x+72+5，
解得x1=−9.4（舍去），x2=−4.6，
∵EF=CD=12，
∴FM=6−4.6=1.4，
∵MG︰FM=2︰7，
∴MG=0.4，
∴点G的坐标为．
将代入y=−59x2+d
解得：m=585
∴OP的最高高度为585米
任务3：如图．
设P(0,m)，∵乙喷水头喷射水柱的最高点与点P的高度差为0.8m
∴从点P喷射的抛物线水柱顶点坐标为，
又∵抛物线形状相同，
∴抛物线表达式为y=−59x−k2+m+0.8，
把P(0,m)代入得m=−59k2+m+0.8，
解得k=−1.2或1.2（舍去），
∴y=−59x+1.22+m+0.8，
∵OP喷出的水柱高度不低于5m，
∴m+0.8>5
∴m>215
又∵要求水柱不能碰到图2中的水柱，也不能落在蓄水池外面．
由（2）可得M−4.6,1.8
代入y=−59x+1.22+m+0.8
即1.8=−59−4.6+1.22+m+0.8
解得：m=33445
∴215∴喷水装置OP高度的变化范围为21515．（2024·河北石家庄·一模）图1为某游乐场过山车的一部分滑道设施，为研究过山车沿滑道运动中的数学知识，小李使用电脑软件将这部分滑道抽象出如图2所示的函数图象，并模拟过山车（抽象为点）的运动．线段AB是一段直滑道，点A在y轴上，且OA=1．滑道B−C−D为抛物线：y=14x2+bx+c的一部分，在点C(4,2)处达到最低，点B，D到x轴的距离相等，其中点B到点A的水平距离为2，BG⊥x轴于点G．滑道B−C−D与滑道D−E−F可看作形状相同、开口方向相反的两段抛物线，点F(12,0)．
(1)求抛物线B−C−D和D−E−F的函数表达式；
(2)当过山车沿滑道从点A运动到点F的过程中，过山车到x轴的距离为1.5时，求它到出发点A的水平距离；
(3)点M为B−C上的一点，求点M到BG和到x轴的距离之和（图中）的最大值及此时点M的坐标．
【答案】(1)B−C−D抛物线的函数表达式为B−C−Dy=14x2−2x+6，D−E−F的函数表达式为y=−14(x−8)2+4
(2)x=0.5或
(3)MH和MN长度之和的最大值为4．此时M的坐标为(4,2)
【分析】本题考查了动点问题的函数图象，熟练掌握待定系数法求函数解析式是关键．
（1）待定系数法求出滑道B−C−D和D−E−F 的解析式即可；
（2）先求出直线AB的解析式，再分析x=1.5时在各段函数上的对应x值，最后计算各点到点A的水平距离即可；
（3）设，则MH=x−2，MN=14(x−4)2+2，整理出关于x的函数解析式，分析判断最值即可得到点M坐标．
【详解】（1）解：滑道B−C−D；y=14x2+bx+c 的顶点为点C(4,2)，
∴y=14(x−4)2+2 即y=14x2−2x+6，
∵点B到点A的水平距离为2，
∴将代入y=14(x−4)2+2，
∴点B(2,3)．
∵点D与点B关于直线x=4对称，
点．
∵滑道B−C−D 与滑道D−E−F 是形状完全相同、开口方向相反的抛物线，
∴可设抛物线D−E−F 的函数表达式为y=−14(x−ℎ)2+k．
将点F(12,0)，分别代入得：
−14(12−ℎ)2+k=0−14(6−ℎ)2+k=3，解得ℎ=8k=4，
∴抛物线D−E−F的函数表达式为y=−14(x−8)2+4；
（2）解：设直线AB的函数表达式为．
将B(2,3)，A(0,1)代入 得：
b=12k+b=3，解得k=1b=1，
∴直线AB的函数表达式为y=x+1．
∵点C(4,2)为抛物线B−C−D 的顶点，
∴抛物线B−C−D 不存在 的点．
当 时，，x=0.5．
1.5=−14(x−8)2+4，
解得，
根据图像可知，
综上所述， 时，过山车到出发点A的水平距离为：x=0.5或；
（3）解：设，则MH=x−2，MN=14(x−4)2+2，
，
∵点M为B−C上一点，
，且的值随x的增大而增大，
∴当x=4时，，
∴当x=4时，MH和MN长度之和的最大值为4．
此时M的坐标为(4,2)．
16．（2024·浙江嘉兴·一模）根据以下素材，探索完成任务．
【答案】任务1：见解析，y=−140x2+x+1；任务2：水流无法喷灌到草坡最远处,理由见解析；任务3：树AB可以被灌溉到，理由见解析；k的取值范围0【分析】本题考查了二次函数的应用，二次函数的平移，解直角三角形的应用，利用数形结合的思想解决问题是解题关键．
任务1：根据题意建立适当的平面直角坐标系，设抛物线的函数表达式为y=ax−202+k，将点0,1、20,11代入求出a、k的值，即可得到抛物线的函数表达式；
任务2：设草坡最远处为点C，过点C作轴于点D，结合坡度解直角三角形，求出CD=4，OD=40，得到C40,4，再求出当时，y的值，比较即可得到答案；
任务3：延长BA交x轴于点M，结合坡度解直角三角形，得到A30,3，再求出当时，y的值，比较即可得到答案．由题意可知，移动后的解析式为y=−140x−20+k2+11，求出，将点A30,3代入解析式求出k的值，即可得到k的取值范围．
【详解】解：任务1：
如图建立平面直角坐标系，
设抛物线的函数表达式为y=ax−202+k，
由图象可知，抛物线过点0,1、20,11，
则400a+k=1k=11，解得：a=−140k=11，
∴抛物线的函数表达式为y=−140x−202+11=−140x2+x+1；
任务2：
水流无法喷灌到草坡最远处,理由如下：
如图，设草坡最远处为点C，过点C作轴于点D，
由题意可知，喷灌架置于坡度为的坡地底部点O处． 草坡的长度为4101米，
∴OC=4101，CD:OD=1:10，
设CD=x，OD=10x，
由题意得：OC=CD2+OD2=101x=4101，
∴x=4，
∴CD=4，OD=40，
∴C40,4，
在抛物线y=−140x2+x+1中，当时，y=−140×1600+40+1=1，
∵1<4，
∴水流无法喷灌到草坡最远处；
任务3：
树AB能否被灌溉到，理由如下：
由题意可知，延长BA交x轴于点M，
由题意可知，，OM=30，
∵坡度为，
∴AM:OM=1:10，
∴AM=3，
∴A30,3，BM=6，
在抛物线y=−140x2+x+1中，当时，y=−140×900+30+1=8.5，
∵8.5>6，
∴树AB可以被灌溉到，
由题意可知，将喷灌架向正后方向移动k米，则移动后的解析式为y=−140x−20+k2+11，
当时，y=−14010+k2+11，
若要使树AB被喷灌到，则−14010+k2+11=3，
解得：k1=85−10，k2=−85−10（舍），
∴017．（2024·辽宁葫芦岛·一模）某厂家特制了一批高脚杯，分为男士杯和女士杯（如图1），相关信息如下：
根据以上素材内容，尝试求解以下问题：
(1)求抛物线DCE和抛物线FCG的解析式；
(2)当杯子水平放置及杯内液体静止时，若男士杯中的液体与女士杯中的液体深度均为4cm，求两者液体最上层表面圆面积之差；（结果保留π）
(3)当杯子水平放置及杯内液体静止时，若男士杯中的液体与女士杯中的液体深度相等，两者液体最上层表面圆面积相差4πcm2，求杯中液体的深度．
【答案】(1)抛物线DCE的解析式为y=25x2+5，抛物线FCG的解析式为：y=85x2+5
(2)154
(3)杯中液体深度为3215cm或185cm
【分析】本题考查二次函数的实际应用．解题的关键是正确的求出函数解析式，利用二次函数的性质，进行求解即可．
（1）设出函数解析式，利用待定系数法求出函数解析式即可；
（2）设男士杯中液体与女士杯中液体最上层表面圆的半径分别为，r,分别求出，r,即可得出结果；
（3）分5≤y≤152和152≤x≤15进行讨论求解即可．
【详解】（1）解：∵点C0,5为抛物线DCE和抛物线FCG的顶点，对称轴为y轴，
∴设抛物线DCE的解析式为：y=a1x2+5，
将点E52,152代入，得152=522a1+5，解得a1=25．
∴抛物线DCE的解析式为：y=25x2+5．
设抛物线FCG的解析式为：y=a2x2+5，将点G52,15代入，
得15=522a2+5，解得a2=85．
∴抛物线FCG的解析式为：y=85x2+5．
（2）解：设男士杯中的液体与女士杯中的液体最上层表面圆的半径分别为Rcm,rcm，
由题可知，当男士杯中的液体与女士杯中的液体深度均为4cm时，R=52．
在抛物线FCG中：将y=5+4=9代入解析式得85x2+5=9，
∴x2=9−5×58=52=r2，
∴两者液体最上层表面圆面积之差为πR2−πr2=522−52=154cm2；
（3）解：设男士杯中的液体与女士杯中的液体最上层表面圆的半径分别为Rcm,rcm，
当5≤y≤152时R2=52y−5,r2=58y−5，
∴πR2−πr2=4π
即52y−5−58y−5=4
解得y=10715．此时深度为10715−5=3215cm．
当152∴πR2−πr2=4π即254−58y−5=4．解得y=435．
此时深度为435−5=185cm．综上所述：杯中液体深度为3215cm或185cm．
18．（2024·河南信阳·二模）安阳市水冶镇附近有一个马氏庄园，庄园中的建筑房顶为悬山顶式构造，独特的屋顶线条设计可以在下雨时保证雨水流下时流到院中地面某处．如图为一栋建筑的侧面示意图，下雨时，雨水顺着房顶AB，经走廊顶部水平管道BC流出，呈抛物线落到院中地面上E点（可视C为抛物线顶点）．若走廊DF和顶部BC的宽度均为1m，屋高BD为3m，雨水落点距屋子的水平距离DE为2m，请根据题意，解决下列问题．
(1)建立合适的坐标系，求出雨水从顶点C落到地面E点的抛物线表达式；
(2)现计划在院中安放一个高为0.9m的圆柱形洗手池，洗手池下面连接储水装置，可以对水资源重复利用，为使下雨时雨水正好可以落在洗手池的顶部中心点，请按设计计算雨水池的底面中心G到墙面的距离DG的长．
【答案】(1)y=−3x2
(2)DG=70+1010
【分析】本题主要考查二次函数的应用：
（1）以点C为原点，BC所在直线为x轴，B→C方向为正方向建立平面直角坐标系，求得E1,−3，设抛物线解析式为y=ax2，运用待定系数法求解即可；
（2）求出点与CF之间的距离即可解决问题．
【详解】（1）解：以点C为原点，BC所在直线为x轴，B→C方向为正方向建立平面直角坐标系，
∵DF=BC=1，DE=2，BD=3，
∴CF=3,EF=1,
∴C0,0，E1,−3.
设抛物线解析式为y=ax2，
∵将点E1,−3代入解析式可得，−3=a×12，
解得a=−3，
∴抛物线的表达式为y=−3x2；
（2）解：若想让雨滴正好落在点，则点需在CE所在的抛物线上，
∵BD=3，HG=0.9，则B与的距离为3−0.9=2.1，
可设Hx,−2.1，Gx,−3，
将Hx,−2.1代入解析式可得，
−2.1=−3x2，
解得x=7010，
∴DG=DF+FG=7010+1=70+1010
19．（2023·河北邯郸·二模）某公园要在小广场建造一个喷泉景观．在小广场中央O处垂直于地面安装一个高为1.25米的花形柱子OA，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，为使水流形状较为美观，设计成水流在距OA的水平距离为1米时达到最大高度，此时离地面2.25米．
(1)以点O为原点建立如图2所示的平面直角坐标系，水流到OA水平距离为x米，水流喷出的高度为y米，求出在第一象限内抛物线的解析式（不要求写出自变量的取值范围）；
(2)张师傅正在喷泉景观内维修设备期间，喷水管意外喷水，但是身高1.76米的张师傅却没有被水淋到，此时他离花形柱子OA的距离为d米，求d的取值范围；
(3)为了美观，在离花形柱子4米处的地面B、C处安装射灯，射灯射出的光线与地面成45°角，如图3，光线交汇点P在花形柱子OA的正上方，其中光线BP所在的直线解析式为y=−x+4，求光线与抛物线水流之间的最小垂直距离．
【答案】(1)y=−x−12+2.25
(2)0.3(3)光线与抛物线水流之间的最小垂直距离为24米
【分析】（1）根据题意得到第一象限内的抛物线的顶点坐标，将抛物线设成顶点式，再将点A坐标代入即可求出第一象限内的抛物线解析式；
（2）直接令y=1.76，解方程求出x的值，再根据函数的图象和性质，求出y>1.76时x的取值范围即可；
（3）先作辅助线，作出直线BP的平行线l，使它与抛物线相切于点D，然后设出直线l的解析式，联立直线与抛物线解析式，利用相切，方程只有一个解，解出直线l的解析式，从而得到直线与x轴交点，最后利用锐角三角函数求出直线l与直线BP之间的距离．
【详解】（1）解：根据题意第一象限内的抛物线的顶点坐标为1,2.25，A0,1.25，
设第一象限内的抛物线解析式为y=ax−12+2.25，
将点A0,1.25代入物线解析式，
1.25=a0−12+2.25，
解得a=−1，
∴第一象限内的抛物线解析式为y=−x−12+2.25；
（2）解：根据题意，令y=1.76，
即−x−12+2.25=1.76，
解得x1=0.3，x2=1.7，
∵−1<0，抛物线开口向下，
∴当0.31.76，
∴d的取值范围为0.3（3）解：作直线BP的平行线l，使它与抛物线相切于点D，分别交x轴，y轴于点E，F，过点E，作EG⊥PB，垂足为G，如图所示，
∵l∥PB，
设直线l的解析式为y=−x+m，
联立直线与抛物线解析式y=−x+my=−x−12+2.25，
整理得x2−3x+m−1.25=0，
∵直线l与抛物线相切，
∴方程只有一个根，
∴Δ=32−4×1×m−1.25=0，
解得m=3.5，
∴直线l的解析式为y=−x+3.5，
令y=0，则x=3.5，
∴E3.5,0，
∴BE=4−3.5=0.5，
即EB=12，
∵射灯射出的光线与地面成45°角，
∴∠EBG=45°，
，
，
∴EG=22×12=24，
∴光线与抛物线水流之间的最小垂直距离为24米．
【分析】本题考查二次函数的应用，求二次函数解析式，二次函数的性质，直线的平移，直线和抛物线相切等知识，解题的关键是求抛物线解析式．
20．（2024·陕西西安·一模）2023年5月28日，C919商业首航完成中国民航商业运营国产大飞机正式起步．12时31分航班抵达北京首都机场，穿过隆重的“水门礼”（寓意“接风洗尘”，是国际民航中高级别的礼仪），如图1，在一次“水门礼”的预演中，两辆消防车从机翼两侧向斜上方喷射水柱，喷射的两条水柱近似看作形状相同的抛物线的一部分，当两辆消防车喷水口A、B的水平距离为80米时，两条水柱恰好在抛物线的顶点处相遇，此时相遇点距地面20米，喷水口A、B距地面均为4米．如图2，以地面两辆消防车所在的直线为x轴，过点所在的铅直线为y轴建立平面直角坐标系．
(1)写出点B、H的坐标，并求出抛物线的关系式；
(2)两辆消防车同时向后移动相同的距离，此时两个水柱的交点记为H'，若，请求出两辆消防车移动的距离．
【答案】(1)，y=−1100x2+20；
(2)两辆消防车应同时向后移动10米．
【分析】此题重点考查二次函数的图象与性质、二次函数的应用等知识，正确地求出二次函数的解析式是解题的关键．
（1）设，将代入求得a的值即可；
（2）由题知OH'=OH−HH'=19，可得． 设平移的后抛物线为， 将点代入求得m的值即可解答．
【详解】（1）由题意得：，
∵H(0,20)为抛物线的顶点，
∴设，
将点代入得：，
解得：a=−1100，
∴y=−1100x2+20；
（2）由题知OH'=OH−HH'=19，
∴H'(0,19)．
同时移动后两条水柱形成的抛物线关于y轴对称，因此H'就是平移后任意一条抛物线与y轴的交点，设右侧消防车向后移动了m米，
则平移的后抛物线为，
将点代入上式，解得：m=10或-10（舍），
因此要使，两辆消防车应同时向后移动10米．
设计喷水方案
素材1
图1为某公园的圆形喷水池，图2是其示意图，O为水池中心，喷头A、B之间的距离为20米，喷射水柱呈抛物线形，水柱距水池中心7m处达到最高，高度为5m，水池中心处有一个圆柱形蓄水池，其底面直径CD为12m，高CF为1.8米


素材2
如图3、图4，拟将在圆柱形蓄水池中心处建一能伸缩高度的喷水装置OPOP⊥CD，要求水柱不能碰到图2中的水柱，也不能落在蓄水池外面．经调研，目前市场有两种喷水头均能喷射与图2中形状相同的抛物线．其中，甲喷水头以点P为最高点向四周喷射水柱(如图3)，乙喷水头喷射水柱的最高点与点P的高度差为0.8m (如图4)．

问题解决
任务1
确定水柱形状
在图2中以点O为坐标原点，水平方向为轴建立直角坐标系，求左边这条抛物线的函数表达式．
任务2
选择喷水装置甲，确定喷水装置的最高高度
若选择甲装置(图3)，为防止水花溅出，当落水点G、M之间的距离满足GM=27FM时，OP不能再升高，求此时OP的最高高度．
任务3
选择喷水装置乙，拟定喷水装置的高度范围
若选择乙装置(图4)，为了美观，要求OP喷出的水柱高度不低于5m，求喷水装置OP高度的变化范围．
素材1
如图1，一个移动喷灌架射出的水流可以近似地看成抛物线． 图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米． 当喷射出水流距离喷水头20米时，达到最大高度11米．
素材2
现将喷灌架置于坡度为1:10的坡地底部点O处． 草坡的长度为4101米．
问题解决
任务1
请在图2中建立适当的平面直角坐标系，并求抛物线的函数表达式．
任务2
当喷灌架底部位于点O处时，请通过计算说明水流能否喷灌到草坡最远处．
任务3
草坡上距离O的水平距离为30米处有一棵高度为3米的树AB需要被喷灌，当喷灌架底部仍然在点O处时，请通过计算说明树AB能否被灌溉到．现将喷灌架向正后方向移动k米，若要使树AB被喷灌到，求k的取值范围．
素材
内容
素材1
如图1，这种高脚杯从下往上分为三部分：
杯托，杯脚，杯体．杯托为一个圆，水平放置时候，杯脚经过杯托圆心，并垂直任意直径，杯体的水平横截面都为圆，这些圆的圆心都在杯脚所在直线上．
素材2
图2坐标系中，特制男士杯可以看作由线段AB，OC，抛物线DCE（实线部分），线段DF，线段EG绕y轴旋转形成的立体图形（不考虑杯子厚度，下同）；特制女士杯可以看作由线段AB，OC，抛物线FCG（虚线部分）绕y轴旋转形成的立体图形
素材3
已知，图2坐标系中，OC=5cm，记为C0,5,D−52,152,E52，152,F−52,15,G52,15．