






还剩35页未读,
继续阅读
所属成套资源:【大单元】鲁教五四版数学九年级下学期课件PPT整套
成套系列资料,整套一键下载
大单元鲁教版数学九年级下册《几何综合》 课件
展开
这是一份大单元鲁教版数学九年级下册《几何综合》 课件,共43页。
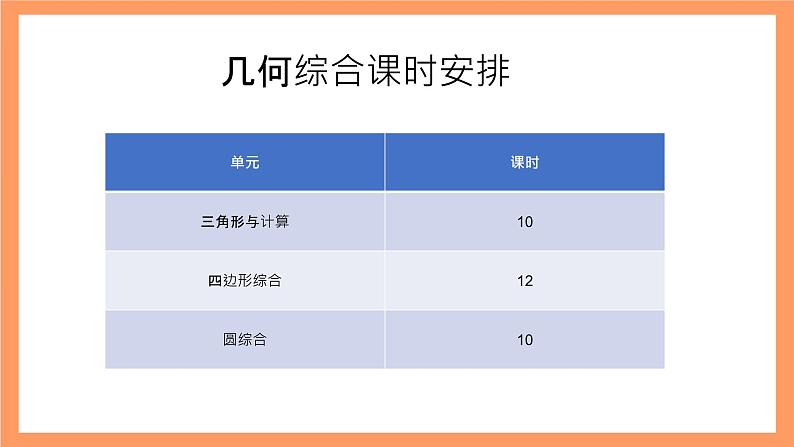
几何综合题鲁教版数学九年级下册几何综合题是中考试卷中常见的题型,大致可分为几何计算型综合题与几何论证型综合题,它主要考查学生综合运用几何知识的能力这类题型在近几年中考试卷中占有相当的分量,不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题.还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂,覆盖面广、涉及的知识点较多题设和结论之间的关系较隐蔽,常常需要添加辅助线来解答几何综合题的呈现形式多样,如折叠类型、探究型、开放型、运动型、情景型等,背景鲜活,具有实用性和创造性,考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力综述【知识与技能目标】(1)掌握三角形全等与三角形相似的性质与判定定理(2)掌握特殊四边形的性质和判定定理,尤其是平行四边形的判定理与菱形的性质定理(3) 掌握圆与直线的位置关系的判定,会求弧长及扇形的面积,圆锥的侧面积。学习目标【过程与方法目标】 (1)会用三角形、四边形圆的性质和判定定理解决相关问题 (2)会用三角形、四边形圆的性质和判定定理解决简单实际问题。 【情感与价值目标】(1)经历由情境引出问题,探索掌握有关数学知识,在运用实践的过程中,培养学生学数学、用数学的意识与能力。(2)感受数学文化的价值和中国传统数学的成就,激发学生热爱祖国悠久文化的思想情感。 单元教学内容专题一:三角形计算与证明专题二:四边形综合专题三:圆几何综合课时安排经过平行线、三角形、四边形、圆等各种图形的推理训练和几何证明训练,学生们已经建立了较强的推理意识、培养了较强的图形观察力,也积累了较丰富的几何模型。这是学生解决几何综合题的有利因素。但由于对各种几何图形的学习是分散在六册书的不同章节,平常都是相对独立地训练某个知识点, 一旦将各类终形和问题综合起来,学生就会感觉复杂而手足无措,不能有逻辑地将大问题细化成小问题,无法通过知识的转化和迁移与平时的练习联系起来,这就造成了学生对于几何综合体无从下手的局面,如何让学生从整体把握问题,学会逐层刨析问题,是几何综合解题中必须要面对的问题。学情分析中考命题的思路方向:中考几何综合题,常以几何图形为载体(有三角形、四边形、圆等,其中以三角形、四边形居多)考查几何或函数知识,常考内容有以下两类:(1)证明类问题。1线段、角的数量关系(包括相等、和差、倍、分关系以及比例关系)。2图形的关系(如三角形的相似与全等,点与线、线与线、线与圆位置关系等)。3图形的形状(如直角三角形、等腰三角形、梯形、平行四边形、矩形、正方形等的判定)。(2)计算类问题。角度的大小、线段的长度、几何图形的周长、面积的大小、定值最值等的计算;与运动联系并建立函数关系式,从而研究函数的图像与性质等。近年中考数学卷中,出现了许多设计精美、格调清新的集阅读理解、操作、猜想于一体的几何综合题,这类试题综合性强,思考方向不确定,对思维的灵活性、深刻性、发散性、独创性有较高的要求,能够有效的考查学生的阅读能力、自主探究能力、分析解决问题的能力和思维创新能力。这类问题给学生设置了一个类似于科学探究发现的数学活动,要求学生在动手操作的基础上,抓住概念,依托定理,从自己熟悉的图形入手观察、分析推理空间想象、归纳和类比进而形成猜想。这类问题要求学生利用运动、变化、发展的观点来分析问题,进而发现结论并进行证明,最后加以应用。从命题形式上看,中考几何综合题常以“动态几何题”和“数学活动类”两种形式体现。本文以近年莆田市初三质量检查、中考试卷中的“数学活动类”问题为例,对中考几何综合题作命题研究与反思。(1)理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性;(2)探索并证明三角形的内角和定理.掌握它的推论:三角形的外角等于与它不相邻的两个内角的和。证明三角形的任意两边之和大于第三边;(3)理解全等三角形的概念,能识别全等三角形中的对应边、对应角;课标要求(4)掌握基本事实:两边及其夹角分别相等的两个三角形全等;(5)掌握基本事实:两角及其夹边分别相等的两个三角形全等;(6)掌握基本事实:三边分别相等的两个三角形全等;(7)证明定理:两角及其中一组等角的对边分别相等的两个三角形全等;(8)探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上;(9)理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段垂直平分线上;(10)了解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两底角相等;底边上的高线、中线及顶角平分线重合。探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形。探索等边三角形的性质定理:等边三角形的各角都等于 60°,及等边三角形的判定定理:三个角都相等的三角形(或有一个角是 60°的等腰三角形)是等边三角形;(11)了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个 锐角互余,直角三角形斜边上的中线等于斜边的一半; (12)探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问; (13)探索并掌握判定直角三角形全等的“斜边、直角边”定理; (14)了解三角形重心的概念. (11)了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个 锐角互余,直角三角形斜边上的中线等于斜边的一半; (12)探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问; (13)探索并掌握判定直角三角形全等的“斜边、直角边”定理; (14)了解三角形重心的概念. 考察了三角形的全等与相似真题变式练习(1)了解多边形的定义,多边形的顶点、边、内角、外角、对角线等概念;探索并掌握多边形内角和与外角和公式. (2)理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系;了解四边形的不稳定性. (3)了解两条平行线之间距离的意义,能度量两条平行线之间的距离.课标要求(4)探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分;探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形. (5)探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形;四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形.正方形具有矩形和菱形的一切性质考点一:多边形(1)多边形的定义:在平面内,由若干条不在同一条直线上的线段;首尾顺次相接组成的封闭图形叫做多边形,在多边形中,组成多边形的各条线段叫做多边形的边,每相邻两条边的公共点叫做多边形的顶点,连接不相邻两个顶点的线段叫做多边形的对角线。(2)多边形的内角和:n边形的内角和=(n-2)180°(3)正多边形:在平面内,内角都相等,边也相等的多边形叫做正多边形.(4)多边形的外角:多边形内角的一边与另一边的反向延长线所组成的角,叫做这个多边形的外角.在多边形的每个顶点处取这个多边形的一个外角,它们 的和叫做多边形的外角和,多边形的外角和都等于360°(5)过n边形的一个顶点共有(n-3)条对角线,n边形共有 条对角线.(6)过n边形的一个顶点将n边形分成(n-2)个三角形.考点梳理考点二:相似多边形(1)定义:对应角相等,对应边成比例的两个多边形叫做相似多边形.(2)相似多边形的性质:①相似多边形的周长的比等于相似比;②相似多边形的对应对角线的比等于相似比;③相似多边形的面积的比等于相似比的平方;④相似多边形的对应对角线相似,相似比等于相似多边形的相似比.考点二:相似多边形(1)定义:对应角相等,对应边成比例的两个多边形叫做相似多边形.(2)相似多边形的性质:①相似多边形的周长的比等于相似比;②相似多边形的对应对角线的比等于相似比;③相似多边形的面积的比等于相似比的平方;④相似多边形的对应对角线相似,相似比等于相似多边形的相似比.真题变式练习1.理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并了解点与圆的位置关系;2.探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧;3.探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理及其推论:圆周角的度数等于它所对弧上的圆心角度数的一半;直径所对的圆周角是直角;90°的圆周角所对的弦是直径;圆内接四边形的对角互补;课标要求4.知道三角形的内心和外心;5.了解直线和圆的位置关系,掌握切线的概念,探索切线与过切点的半径的关系,会用三角尺过圆上一点画圆的切线;6.会计算圆的弧长、扇形的面积;7.了解正多边形的概念及正多边形与圆的关系真题变式练习在新课改的背景下,数学学科将目光聚焦于培养学生的学科素养上,保证为“立人”而教,坚持以“育人”为目标,考虑学生已有的认知,顺应学生的思维发展状况与年龄特点,充分体现了学生在数学学习中的主体地位。。大单元教学对数学学科的意义尤为重要,有利于促进学生数学思维的养成,拓展学生的思维空间,帮助学生用数学的眼光认识世界、思考世界,对学生的数学学习具有深远的影响。课程结束
几何综合题鲁教版数学九年级下册几何综合题是中考试卷中常见的题型,大致可分为几何计算型综合题与几何论证型综合题,它主要考查学生综合运用几何知识的能力这类题型在近几年中考试卷中占有相当的分量,不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题.还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂,覆盖面广、涉及的知识点较多题设和结论之间的关系较隐蔽,常常需要添加辅助线来解答几何综合题的呈现形式多样,如折叠类型、探究型、开放型、运动型、情景型等,背景鲜活,具有实用性和创造性,考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力综述【知识与技能目标】(1)掌握三角形全等与三角形相似的性质与判定定理(2)掌握特殊四边形的性质和判定定理,尤其是平行四边形的判定理与菱形的性质定理(3) 掌握圆与直线的位置关系的判定,会求弧长及扇形的面积,圆锥的侧面积。学习目标【过程与方法目标】 (1)会用三角形、四边形圆的性质和判定定理解决相关问题 (2)会用三角形、四边形圆的性质和判定定理解决简单实际问题。 【情感与价值目标】(1)经历由情境引出问题,探索掌握有关数学知识,在运用实践的过程中,培养学生学数学、用数学的意识与能力。(2)感受数学文化的价值和中国传统数学的成就,激发学生热爱祖国悠久文化的思想情感。 单元教学内容专题一:三角形计算与证明专题二:四边形综合专题三:圆几何综合课时安排经过平行线、三角形、四边形、圆等各种图形的推理训练和几何证明训练,学生们已经建立了较强的推理意识、培养了较强的图形观察力,也积累了较丰富的几何模型。这是学生解决几何综合题的有利因素。但由于对各种几何图形的学习是分散在六册书的不同章节,平常都是相对独立地训练某个知识点, 一旦将各类终形和问题综合起来,学生就会感觉复杂而手足无措,不能有逻辑地将大问题细化成小问题,无法通过知识的转化和迁移与平时的练习联系起来,这就造成了学生对于几何综合体无从下手的局面,如何让学生从整体把握问题,学会逐层刨析问题,是几何综合解题中必须要面对的问题。学情分析中考命题的思路方向:中考几何综合题,常以几何图形为载体(有三角形、四边形、圆等,其中以三角形、四边形居多)考查几何或函数知识,常考内容有以下两类:(1)证明类问题。1线段、角的数量关系(包括相等、和差、倍、分关系以及比例关系)。2图形的关系(如三角形的相似与全等,点与线、线与线、线与圆位置关系等)。3图形的形状(如直角三角形、等腰三角形、梯形、平行四边形、矩形、正方形等的判定)。(2)计算类问题。角度的大小、线段的长度、几何图形的周长、面积的大小、定值最值等的计算;与运动联系并建立函数关系式,从而研究函数的图像与性质等。近年中考数学卷中,出现了许多设计精美、格调清新的集阅读理解、操作、猜想于一体的几何综合题,这类试题综合性强,思考方向不确定,对思维的灵活性、深刻性、发散性、独创性有较高的要求,能够有效的考查学生的阅读能力、自主探究能力、分析解决问题的能力和思维创新能力。这类问题给学生设置了一个类似于科学探究发现的数学活动,要求学生在动手操作的基础上,抓住概念,依托定理,从自己熟悉的图形入手观察、分析推理空间想象、归纳和类比进而形成猜想。这类问题要求学生利用运动、变化、发展的观点来分析问题,进而发现结论并进行证明,最后加以应用。从命题形式上看,中考几何综合题常以“动态几何题”和“数学活动类”两种形式体现。本文以近年莆田市初三质量检查、中考试卷中的“数学活动类”问题为例,对中考几何综合题作命题研究与反思。(1)理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性;(2)探索并证明三角形的内角和定理.掌握它的推论:三角形的外角等于与它不相邻的两个内角的和。证明三角形的任意两边之和大于第三边;(3)理解全等三角形的概念,能识别全等三角形中的对应边、对应角;课标要求(4)掌握基本事实:两边及其夹角分别相等的两个三角形全等;(5)掌握基本事实:两角及其夹边分别相等的两个三角形全等;(6)掌握基本事实:三边分别相等的两个三角形全等;(7)证明定理:两角及其中一组等角的对边分别相等的两个三角形全等;(8)探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上;(9)理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段垂直平分线上;(10)了解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两底角相等;底边上的高线、中线及顶角平分线重合。探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形。探索等边三角形的性质定理:等边三角形的各角都等于 60°,及等边三角形的判定定理:三个角都相等的三角形(或有一个角是 60°的等腰三角形)是等边三角形;(11)了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个 锐角互余,直角三角形斜边上的中线等于斜边的一半; (12)探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问; (13)探索并掌握判定直角三角形全等的“斜边、直角边”定理; (14)了解三角形重心的概念. (11)了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个 锐角互余,直角三角形斜边上的中线等于斜边的一半; (12)探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问; (13)探索并掌握判定直角三角形全等的“斜边、直角边”定理; (14)了解三角形重心的概念. 考察了三角形的全等与相似真题变式练习(1)了解多边形的定义,多边形的顶点、边、内角、外角、对角线等概念;探索并掌握多边形内角和与外角和公式. (2)理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系;了解四边形的不稳定性. (3)了解两条平行线之间距离的意义,能度量两条平行线之间的距离.课标要求(4)探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分;探索并证明平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形. (5)探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形;四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形.正方形具有矩形和菱形的一切性质考点一:多边形(1)多边形的定义:在平面内,由若干条不在同一条直线上的线段;首尾顺次相接组成的封闭图形叫做多边形,在多边形中,组成多边形的各条线段叫做多边形的边,每相邻两条边的公共点叫做多边形的顶点,连接不相邻两个顶点的线段叫做多边形的对角线。(2)多边形的内角和:n边形的内角和=(n-2)180°(3)正多边形:在平面内,内角都相等,边也相等的多边形叫做正多边形.(4)多边形的外角:多边形内角的一边与另一边的反向延长线所组成的角,叫做这个多边形的外角.在多边形的每个顶点处取这个多边形的一个外角,它们 的和叫做多边形的外角和,多边形的外角和都等于360°(5)过n边形的一个顶点共有(n-3)条对角线,n边形共有 条对角线.(6)过n边形的一个顶点将n边形分成(n-2)个三角形.考点梳理考点二:相似多边形(1)定义:对应角相等,对应边成比例的两个多边形叫做相似多边形.(2)相似多边形的性质:①相似多边形的周长的比等于相似比;②相似多边形的对应对角线的比等于相似比;③相似多边形的面积的比等于相似比的平方;④相似多边形的对应对角线相似,相似比等于相似多边形的相似比.考点二:相似多边形(1)定义:对应角相等,对应边成比例的两个多边形叫做相似多边形.(2)相似多边形的性质:①相似多边形的周长的比等于相似比;②相似多边形的对应对角线的比等于相似比;③相似多边形的面积的比等于相似比的平方;④相似多边形的对应对角线相似,相似比等于相似多边形的相似比.真题变式练习1.理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并了解点与圆的位置关系;2.探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧;3.探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理及其推论:圆周角的度数等于它所对弧上的圆心角度数的一半;直径所对的圆周角是直角;90°的圆周角所对的弦是直径;圆内接四边形的对角互补;课标要求4.知道三角形的内心和外心;5.了解直线和圆的位置关系,掌握切线的概念,探索切线与过切点的半径的关系,会用三角尺过圆上一点画圆的切线;6.会计算圆的弧长、扇形的面积;7.了解正多边形的概念及正多边形与圆的关系真题变式练习在新课改的背景下,数学学科将目光聚焦于培养学生的学科素养上,保证为“立人”而教,坚持以“育人”为目标,考虑学生已有的认知,顺应学生的思维发展状况与年龄特点,充分体现了学生在数学学习中的主体地位。。大单元教学对数学学科的意义尤为重要,有利于促进学生数学思维的养成,拓展学生的思维空间,帮助学生用数学的眼光认识世界、思考世界,对学生的数学学习具有深远的影响。课程结束
相关资料
更多









