高中数学北师大版 (2019)选择性必修 第一册4.1 直线与圆锥曲线的交点优质课件ppt

这是一份高中数学北师大版 (2019)选择性必修 第一册4.1 直线与圆锥曲线的交点优质课件ppt，共30页。PPT课件主要包含了代数方法，直线与椭圆的位置关系，不平行，直线与抛物线位置关系，数形结合，相交一个交点，相交于两个点，图象法，相交与一个点，得到一元一次方程等内容，欢迎下载使用。

回忆：直线与圆的位置关系
1.位置关系：相交、相切、相离2.判别方法(代数法) 联立直线与圆的方程 消元得到二元一次方程组 (1)△>0直线与圆相交有两个公共点； (2)△=0 直线与圆相切有且只有一个公共点； (3)△<0 直线与圆相离无公共点．
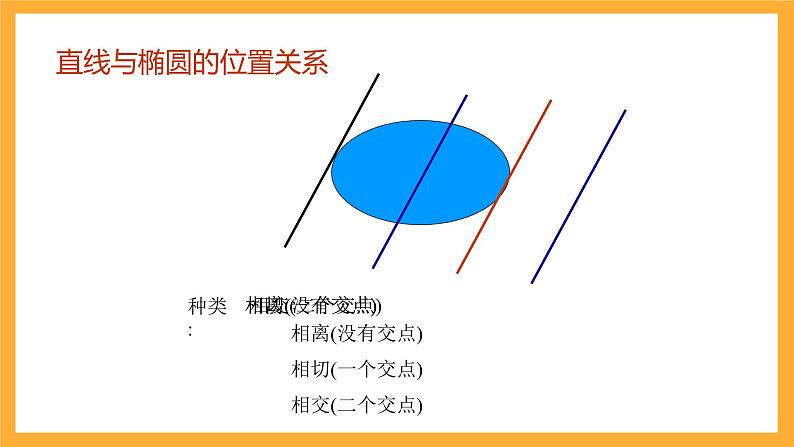
相离(没有交点)相切(一个交点)相交(二个交点)
直线与椭圆的位置关系的判定
1.位置关系：相交、相切、相离2.判别方法(代数法) 联立直线与椭圆的方程 消元得到二元一次方程组 (1)△>0直线与椭圆相交有两个公共点； (2)△=0 直线与椭圆相切有且只有一个公共点； (3)△<0 直线与椭圆相离无公共点．
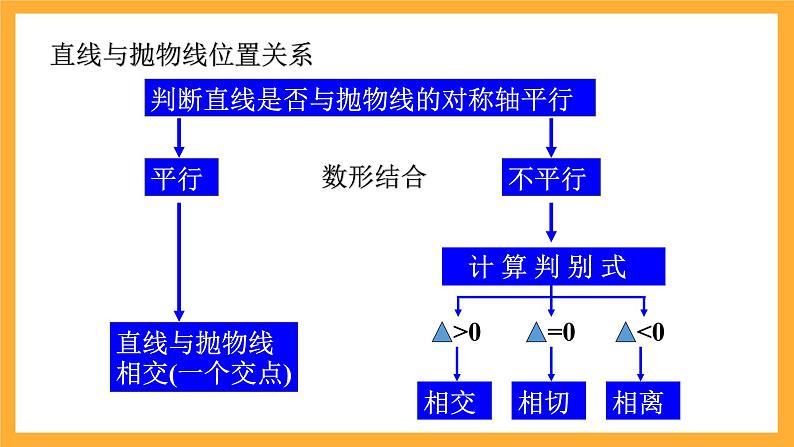
判断直线是否与抛物线的对称轴平行
直线与抛物线相交(一个交点)
计 算 判 别 式
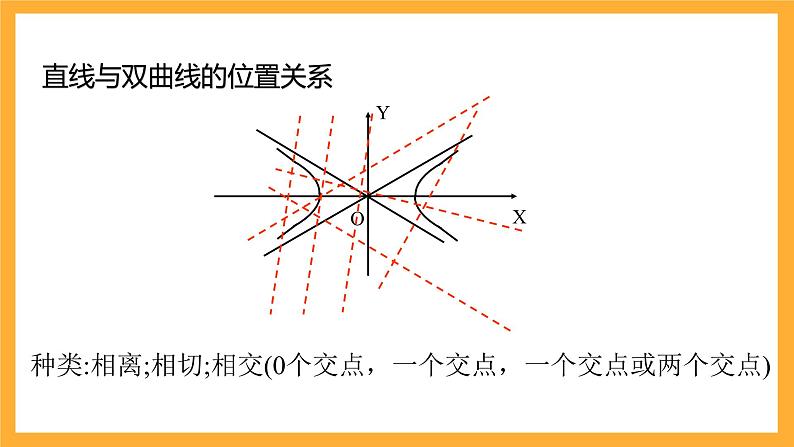
直线与双曲线的位置关系
种类:相离;相切;相交(0个交点，一个交点，一个交点或两个交点)
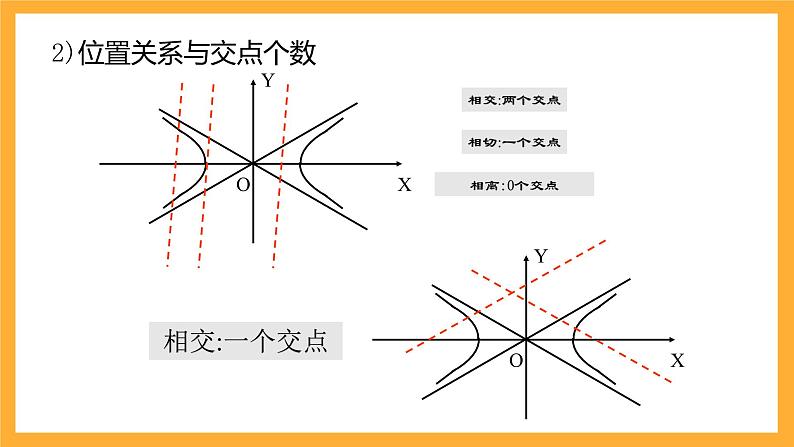
2)位置关系与交点个数
[1] 0 个交点和两个交点的情况都正常,依然可以用判别式判断位置关系
[2]一个交点却包括了两种位置关系:相切和相交 ( 特殊的相交 ) , 那么是否意味着判别式等于零时 , 即可能相切也可能相交 ?
把直线方程代入抛物线方程
直线与抛物线的对称轴平行
代数法:判断直线与抛物线位置关系的操作流程图
①若a=0,当圆锥曲线是双曲线时,直线l与双曲线的渐近线平行或重合;当圆锥曲线是抛物线时,直线l与抛物线的对称轴平行(或重合).②若a≠0,设Δ=b2-4ac.Δ>0时,直线和圆锥曲线相交于不同两点;Δ=0时,直线和圆锥曲线相切于一点;Δ<0时,直线和圆锥曲线没有公共点.
斜率为1的直线经过y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.
设A和B的横坐标分别为x1和x2
则|AF|=x1+1, |BF|=x2+1
∴|AB|=x1+x2+2
由条件知直线AB的方程为y=x-1
变式3.（1）过点(-1,0)的直线l 与抛物线y2=6x有公共点, 则直
线l 的斜率的范围是___________.
(3).若直线L:y=ax+1与双曲线: 3x2-y2=1的左、右两支各有一个公共点,则实数a的取值范围是 .
“画图”是解题的首要环节.
变式4、在抛物线y2=64x上求一点，使它到直线Ｌ:4x+3y+46=0的距离最短，并求此距离.
直线与圆锥曲线的位置关系
1.直线与椭圆的位置关系:
设直线与椭圆方程分别为: y=kx+m与 :
消去y得: Ax2+Bx+C=0
2.直线与双曲线的位置关系:
设直线与双曲线方程分别为: y=kx+m与 :
(1)若直线与渐近线平行, 则相交且只有一个交点.
(2)若直线与渐近线重合, 则相离即没有交点.
(3)若直线与渐近线相交,
3.直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若直线与对称轴相交,
直线与抛物线或双曲线有一个公共点就是直线与抛物线或双曲线相切吗？
判断直线与曲线位置关系的操作程序
把直线方程代入曲线方程
直线与双曲线的渐近线或抛物线的对称轴平行