高中数学北师大版 (2019)选择性必修 第一册2.2 空间向量的运算优秀ppt课件

这是一份高中数学北师大版 (2019)选择性必修 第一册2.2 空间向量的运算优秀ppt课件，共27页。PPT课件主要包含了知识回顾，新课探究，横纵竖，应用4判定垂直，巩固提升，距离公式，课堂小结等内容，欢迎下载使用。
①空间任意三个不共面的向量都可以构成空间的一组基． ②三个向量不共面就隐含着它们都不是零向量。（零向量与任意非零向量共线，与任意两个非零向量共面）。 ③一组基是不共面的三个向量构成的一个向量组，一个基向量是指基中的某一个向量。
几个基本概念：空间任一向量均可以由空间不共面的三个向量生成，我们把｛a、b、c｝叫做空间的一组基，
a、b、c都叫做基向量．
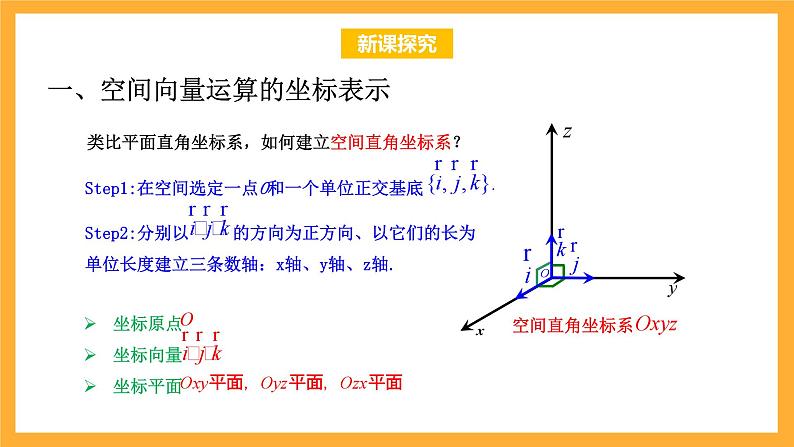
类比平面直角坐标系，如何建立空间直角坐标系？
坐标原点坐标向量坐标平面
一、空间向量运算的坐标表示
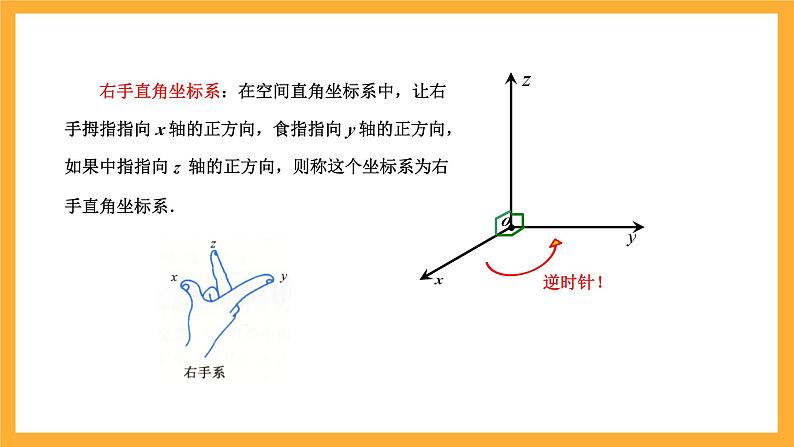
右手直角坐标系：在空间直角坐标系中，让右手拇指指向 x 轴的正方向，食指指向 y 轴的正方向，如果中指指向 z 轴的正方向，则称这个坐标系为右手直角坐标系．
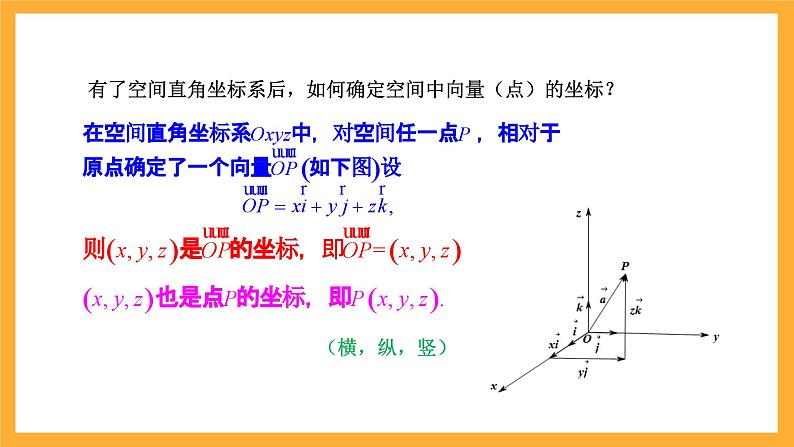
有了空间直角坐标系后，如何确定空间中向量（点）的坐标？
1.建立空间直角坐标系的叙述规范
2.建立空间直角坐标系的原则
以…为原点，以…所在直线为x、y、z轴，建立如图空间直角坐标系.（图上务必标出）
有垂直用垂直，无垂直作垂直；使尽可能多的点落在坐标轴上或坐标平面内.
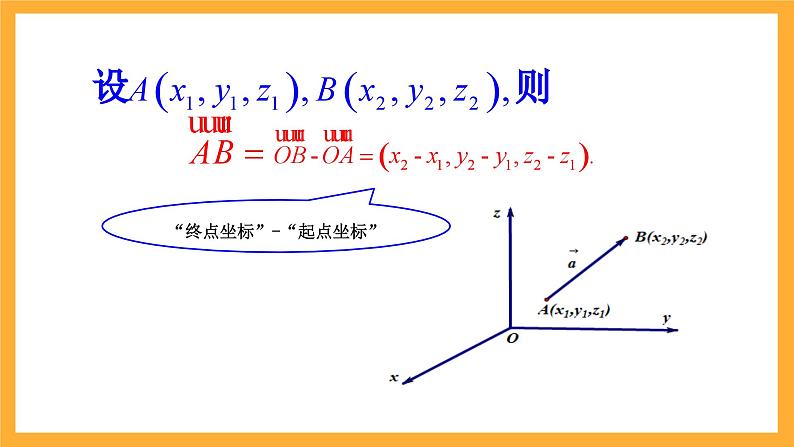
“终点坐标”-“起点坐标”
类比平面向量，我们能利用空间向量的坐标解决哪些问题？
二、空间向量平行（共线）和垂直的条件
2.设a＝(1，y，－2)，b＝(－2，－4，z)，若a∥b，则y＝________，z＝________．
3.已知a＝(1，－5，6)，b＝(0，6，5)，则a与b(　　)A．垂直　　 B．不垂直也不平行C．平行且同向 D．平行且反向解析：选A. a·b＝(1，－5，6)·(0，6，5)＝－5×6＋5×6＝0.∴a⊥b.
4.设a＝(1，0，1)，b＝(1，－2，2)，则〈a，b〉＝________．
（1）向量的长度（模）公式
注意：此公式的几何意义是表示长方体的对角线的长度。
三、空间向量长度和夹角的坐标表示
（2）空间两点间的距离公式
1、空间向量的坐标运算；2、利用向量的坐标运算判断空间几何关系的关键：首先要选定单位正交基，进而确定各向量的坐标，再利用向量的坐标运算确定几何关系。