高中数学北师大版 (2019)选择性必修 第一册4.2 二项式系数的性质精品课件ppt

这是一份高中数学北师大版 (2019)选择性必修 第一册4.2 二项式系数的性质精品课件ppt，共42页。PPT课件主要包含了二项式系数的性质，赋值法等内容，欢迎下载使用。

1.二项式定理的内容:
3.二项展开式的通项Tk+1=
针对(a+b)n的标准形式而言
(b+a)n，(a-b)n的通项则分别为:
《详解九章算法》中记载的表
1．“杨辉三角”的来历及规律
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
…… …… ……
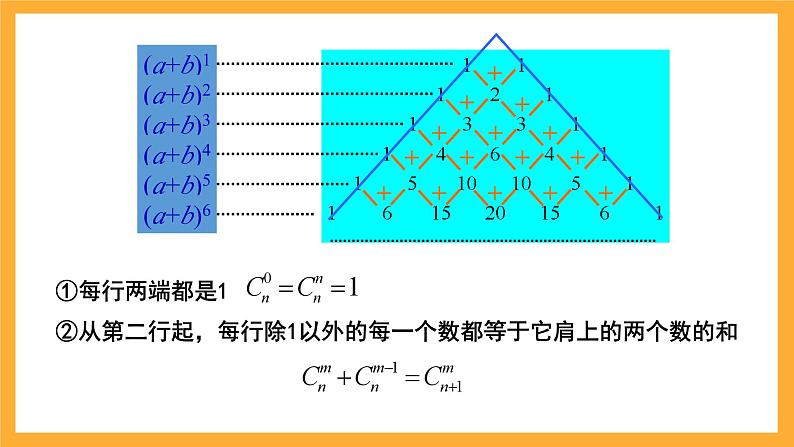
①每行两端都是1②从第二行起，每行除1以外的每一个数都等于它肩上的两个数的和
(1)递推性:除1以外的每一个数都等于它肩上两个数的和.
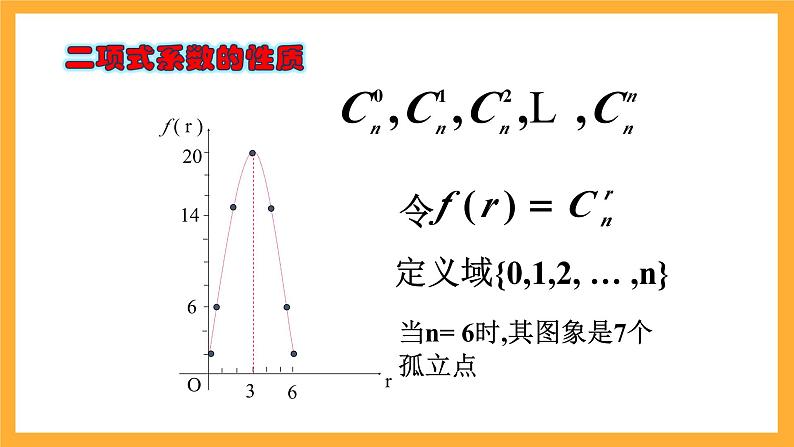
定义域{0,1,2, … ,n}
当n= 6时,其图象是7个孤立点
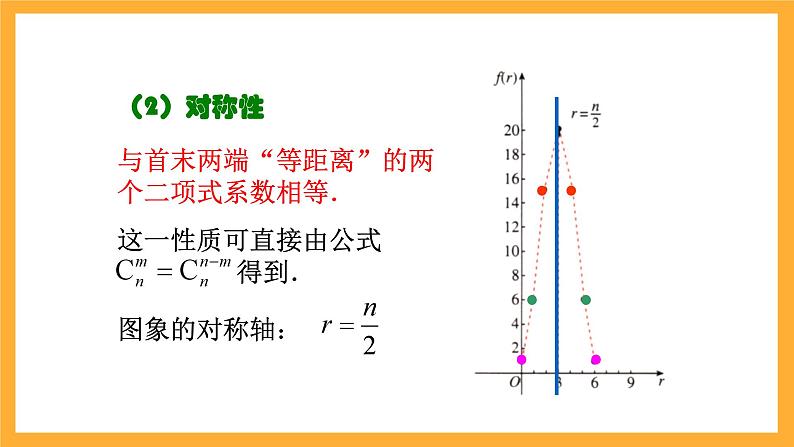
与首末两端“等距离”的两个二项式系数相等．
1、在(a＋b)20展开式中，与第五项的系数相同的项是( ).
A 第15项 B 第16项 C 第17项 D 第18项
2、在(1＋x)10展开式中，与第五项的系数相同的项是_______.
3、(a+b)n展开式中第四项与第六项的系数相等，则n为______.
（3）增减性与最大值
思考：为什么二项式的系数具有“先增后降”的增减性？
二项式系数是逐渐增大的，由对称性可知它的后半部分是逐渐减小的，且中间项取得最大值。
3. 展开式中，只有第6项系数最大，求展开式中的常数项
1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
小结：赋值法在二项式定理中，常对a,b赋予一些特 定的值1，-1等来整体得到所求。
例2 证明在 的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和．
性质4:(a+b)n 的展开式的所有二项式系数的和等于2n.
性质5：在(a+b)n展开式中，奇数项的二项式系数和等于偶数项的二项式系数和.即：
例3、若 的展开式中，所有奇数项 的系数之和为1024，求它的中间项.
解：∵展开式中各项的二项式系数与该项的 的系数相等
∴由已知可得：2n-1=1024
解得 n=11，∴有两个中间项分别为
T6=462x-4，T7=462x
2．(1－2x)15的展开式中的各项系数和是(　　)A．1 B．－1C．215 D．315
解析：令x＝1得各项系数和为－1.
3．若(1＋3x)n的展开式中，第3项的二项式系数为6，则第4项的系数为(　　)A．4 B．27C．36 D．108
4．(2x－1)6展开式中各项系数的和为 ；各项的二项式系数和为________．
解析：令展开式左、右两边x＝1，得各项系数和为1；各二项式系数之和为26＝64.
赋值法的应用—解决二项式系数问题.
小结：求奇次项系数之和与偶次项系数的和可以先赋值，然后解方程组整体求解
例6.在(3x -2y)20的展开式中，求：(1)系数绝对值最大的项;(2)系数最大的项;
（2）因为系数为正的项为奇数项，故可设第2r-1项系数最大。（以下同2） r=5.
1、在(a＋b)20展开式中，与第五项二项式系数相同的项是( ).
A.第6项 B.第7项 C.第6项和第7项 D.第5项和第7项
A.第15项 B.第16项 C.第17项 D.第18项
2、在(a＋b)11展开式中，二项式系数最大的项( ).
5.( 1﹣x ) 13 的展开式中系数最小的项是 （ ）(A)第六项 (B)第七项 （C）第八项 (D)第九项
6.一串装饰彩灯由灯泡串联而成，每串有20个灯泡，只要有一个灯泡坏了，整串灯泡就不亮，则因灯泡损坏致使一串彩灯不亮的可能性的种数为 （ ）(A)20 (B)219 （C）220 (D)220 － 1
1、二项式系数的性质：
3、解决二项式系数和（项的系数和）问题：