高中数学北师大版 (2019)必修 第一册3.1 从频数到频率优秀ppt课件

这是一份高中数学北师大版 (2019)必修 第一册3.1 从频数到频率优秀ppt课件，共29页。PPT课件主要包含了导入课题，频数与频率，新知探究，典例剖析，频率分布直方图的绘制，课堂小结，课后作业等内容，欢迎下载使用。

前面已经介绍了收集数据的一些方法：简单随机抽样(抽签法、随机数法)、分层随机抽样)； 一旦数据被收集上来，我们就可以从中找出需要的信息，通过样本数据的特征，估计总体的相应特征，以此就可以做出恰当的判断. 那么，数据被收集上来后，我们怎么才能更高效地找出需要的信息呢？ 本节我们就一起来学习如何更加高效地整理数据——从频数到频率、频率分布直方图.
频数：将样本按一定的方法分成若干组，每组内含有的个体数目叫作频数.频率：频数与总数的比值称为频率，它能更好地反映样本和总体的相应特征.例如：情景1，某工厂生产一批产品，经调查只有10个不合格产品， 情景2 ，某工厂生产一批产品，经调查产品不合格率为1％. 这两种情景，那种能更好地反映工厂的生产情况呢？ 显然，情景2能更好地反映工厂的生产情况. 原因是：“生产100个产品有10个不合格产品”与“生产10000个产品有10个不合格产品“这两种情况，工厂的生产情况是完全不同的，因此只知道频数是不够的，需要用频率来刻画.
注意：①频数和频率都可以客观地反映总体分布，②但频率反映的是相对总数而言的相对强度，其所带的总体信息远超过频数；③如果总体容量比较小，频数也可以较客观地反映总体分布，④当总体容量较大时，频率才更能客观地反映总体分布.
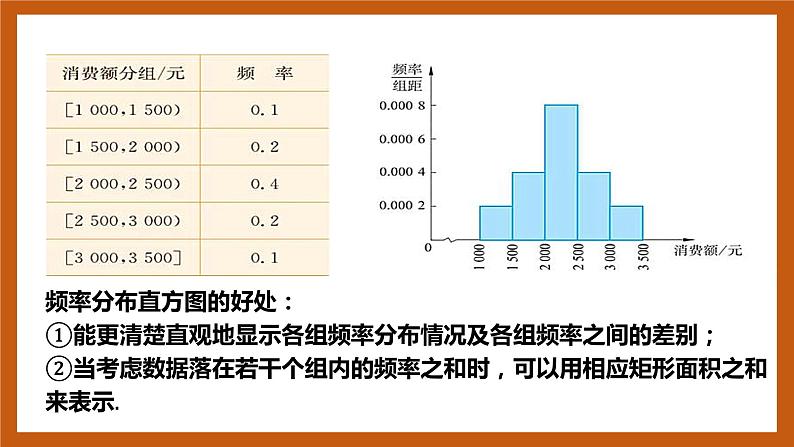
频率分布直方图的好处：①能更清楚直观地显示各组频率分布情况及各组频率之间的差别；②当考虑数据落在若干个组内的频率之和时，可以用相应矩形面积之和来表示.
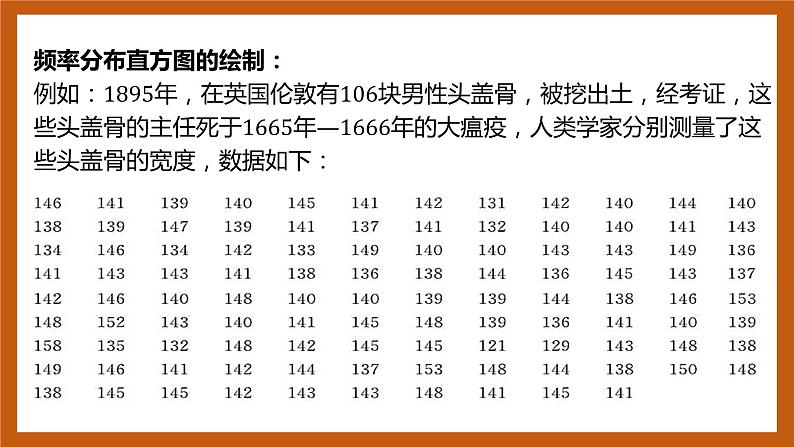
频率分布直方图的绘制：例如：1895年，在英国伦敦有106块男性头盖骨，被挖出土，经考证，这些头盖骨的主任死于1665年—1666年的大瘟疫，人类学家分别测量了这些头盖骨的宽度，数据如下：
4，列表，统计出各组信息，如下表，
频率折线图：在频率分布直方图中，按照分组原则，再在左边和右边各加一个区间．从所加的左边区间的中点开始，用线段依次连接各个矩形的顶端中点，直至右边所加区间的中点，就可得到一条折线，这条折线称为频率折线图．
例1 下表是某两名篮球运动员在中国男子篮球职业联赛(CBA)某个赛季的得分情况统计.
由表得，两名运动员的参赛场次相同，甲、乙的二分球命中总个数(频数)分别为213和160，甲比乙多，但甲、乙的二分球命中率(频率)分别为51％、52％，甲比乙低；因此可认为乙的二分球得分水平更高；同理还可得出甲的三分球得分水平更高.
例2 下面给出了2012年-2016年我国普通高等学校和高中新生录取人数及其相应的录取比例，请根据下表中的数据说明频数与频率的不同之处.
由表得，从2012年-2016年，普通高等学校招生人数及相应的招生比例都在逐年递增，普通高中招生人数基本呈逐年下降趋势，其相应的招生比例基本呈逐年上升趋势.
练习1：一位植物学家想要研究某类植物生长1年之后的高度，他随机抽取了60株此类植物，测得它们生长1年之后的高度如下(单位:cm)：
（1）完成下表： 6 0.1 0.01 8 0.133 0.0133 15 0.25 0.025 17 0.284 0.0284 8 0.133 0.013 6 0.1 0.01 （2）根据上表画出相应的频率分布直方图和折线图，并描述此类植物生长1年之后的高度分布情况.
6 0.1 0.01 8 0.133 0.013315 0.25 0.02517 0.284 0.0284 8 0.133 0.013 6 0.1 0.01
思考1：某中学为了了解九年级学生中女生的身高(单位：cm)情况，对部分九年级女生的身高进行了一次测量，所得数据整理后列出的频率分布表如下：(1)求表中m，n，M，N的值；(2)画出频率分布直方图．
(2)画出频率分布直方图．
思考2：如图是根据部分城市某年6月份的平均气温(单位：℃)数据得到的样本频率分布直方图，其中平均气温的范围是[20.5,26.5]．样本数据的分组为[20.5,21.5)，[21.5，22.5)，[22.5,23.5)，[23.5,24.5)，[24.5,25.5)，[25.5，26.5]．已知样本中平均气温低于22.5 ℃的城市个数为11，求样本中平均气温不低于25.5 ℃的城市个数．解：样本中平均气温低于22.5 ℃的城市的频率为0.10×1＋0.12×1＝0.22，样本中的城市总个数为11÷0.22＝50，样本中平均气温不低于25.5 ℃的城市的频率为0.18×1＝0.18，则样本中平均气温不低于25.5 ℃的城市个数为50×0.18＝9.
思考4：如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图，求估计这次数学竞赛的及格率.解：依题意知大于或等于60分的共四组，它们是[59.5，69.5)，[69.5,79.5)，[79.5,89.5)，[89.5,99.5]，故样本中60分及以上的频率为(0.015＋0.03＋0.025＋0.005)×10＝0.75.由此可估计这次数学竞赛的及格率为75%.
思考5：中小学生的视力状况受到社会的关注．某市有关部门从全市6万名高一学生中随机抽取400名学生，对他们的视力状况进行一次调查统计，将所得到的有关数据绘制成频率分布直方图，如图所示，从左至右五个小组的频率之比为5:7:12:10:6，求这抽取的400名高一学生中视力在[3.95,4.25)范围内的学生人数．
解：由图可知，第五小组的频率为0.5×0.3＝0.15，所以第一小组的频率为0.15×＝0.125，所以这抽取的400名高一学生中视力在[3.95,4.25)范围内的学生有400×0.125＝50(人)．
一，频数与频率二，频率分布直方图三，频率折线图
作业1：课本P167 A组T1